考虑电压相位的实用负荷模型参数辨识

孙 冉，刘利国，黄 桦，陈 谦，鞠 平

（1.河南省电力公司 调度通信中心，河南 郑州 450052；2.河海大学 可再生能源发电技术教育部工程研究中心，江苏 南京 210098）

电力负荷模型对电力系统动态行为有显著影响，对潮流计算、短路计算、安全分析、电压稳定也有一定影响，在临界状态下，还有可能从根本上改变定性结论［1－7］.因此，负荷模型结构及负荷参数辨识研究十分重要.

电力负荷建模的主要方法之一是总体测辨法，已经取得大量成果［8－19］.电力负荷模型结构有间接考虑配电网的经典负荷模型（CLM）和直接考虑配电网的综合负荷模型（SLM）［8－11］，其中电动机通常都采用实用模型.在以往的实际工程应用中，通常只能够测量电压的有效值，无法获得电压相角，从而不得不忽略电压相角或者忽略电压交轴分量的影响.结果表明参数辨识精度不高而且不平稳，功率曲线拟合不够好，尤其在突变点拟合误差明显.

早在1996年，笔者就指出了电压相角对负荷建模的影响［2］：①相角变化对静态负荷没有影响；②相角的缓慢变化对负荷功率影响很小；③相角变化对无功功率影响很小；④由于网络操作或者故障引起相角的急剧变化，对于感应电动机等旋转负荷的有功功率具有不可忽略的影响；⑤电压幅值阶跃变化引起的有功功率变化通常为指数型，而电压相角阶跃变化引起的有功功率变化经常为振荡型.

笔者分析表明，忽略电压相角的影响与忽略电压交轴分量的影响相关联.在大多数情况下，令电压相角为0或者交轴电压分量为0的假设条件并不严格成立.在此基础上，分别采用只考虑电压有效值和考虑交直轴电压分量的2种实用模型，进行参数辨识和拟合效果对比.结果表明，交轴电压分量对辨识结果影响较大，采用交轴电压分量的实用模型能够取得高精度的参数辨识结果和理想的曲线拟合效果.

1 实用负荷模型

在电动机详细Park模型的基础上，忽略定子的电磁暂态过程，再定义实用变量，即可获得电动机的实用模型［11，20－23］.其电势方程为

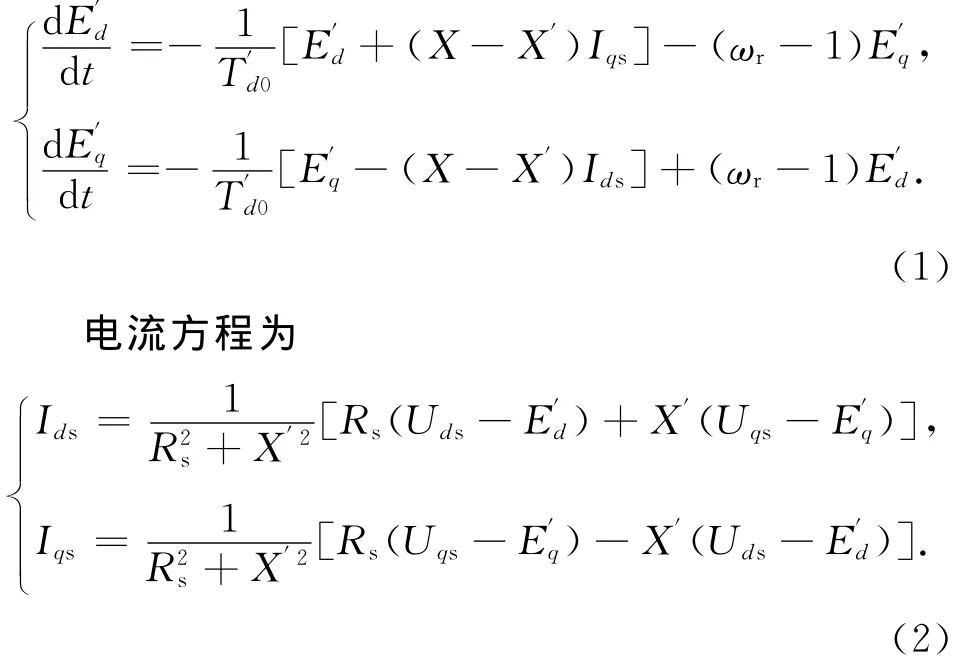
转子运动方程为

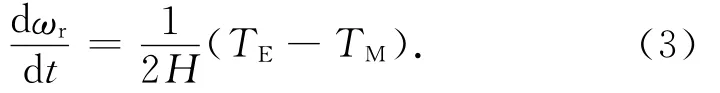
功率方程为

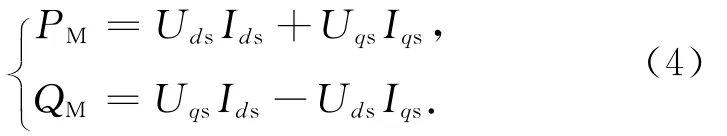
式（1）～（4）方程中，忽略了对转矩几乎没有影响的零轴电压分量，但考虑了交直轴电压分量.

负荷模型中静态部分的功率方程为

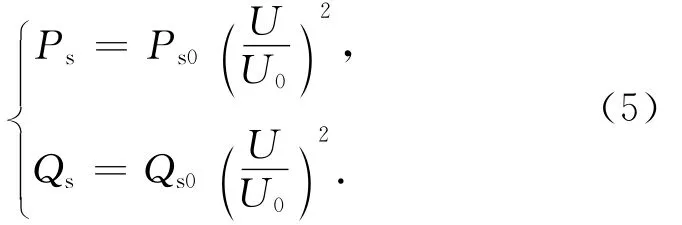
式（1）～（5）不妨称之为双分量实用模型.但以往进行负荷模型参数辨识时，由于测量条件限制，尤其是采用模拟量数据采集方式时，只能够获得电压有效值.故简化假设：

将式（6）代入式（1）～（5），即可得到单分量实用模型［11］.其电势方程变为

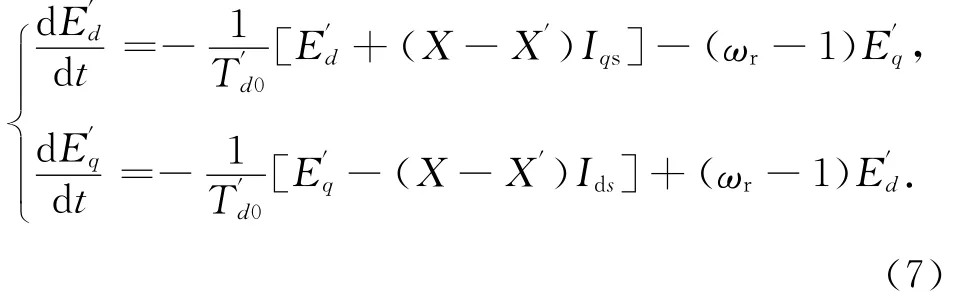
电流方程变为

电动机功率方程变为

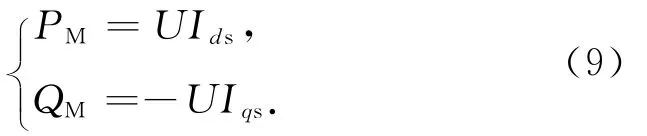
其余方程保持不变.

2 近似条件分析

单分量实用模型的前提条件是式（6），即假设在整个动态过程中，交轴电压分量为0，而只有直轴电压分量.abc坐标系统转换为dq坐标系统如图1所示［20－21］，其中

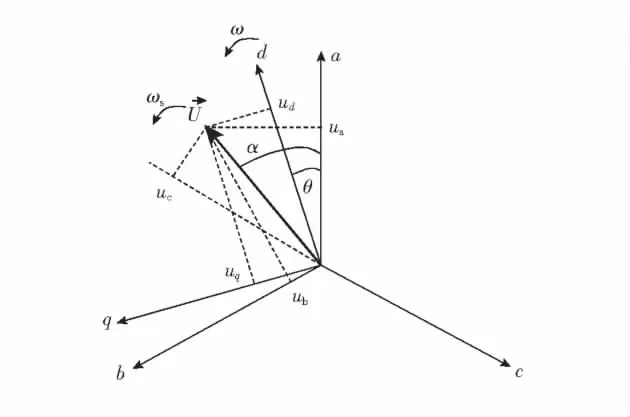
图1 abc系统与dq系统坐标示意Figure 1 abc and dqsystems diagram

相应的Park变换公式为

由图1可见，要使交轴电压分量在整个动态过程中均为0，必须使电压矢量与d轴始终重合，即α＝θ，再结合式（10），需要满足条件：①2个坐标系统始终以相同的角速度旋转，即ω＝ωs，这是保证整个动态过程中交轴电压分量为0的前提；②t＝0时，d轴与a轴重合，即θ0＝0，这是交轴电压分量为0的初始条件；③a，b，c三相电压对称，即幅值相等、相位互差120°，至少应满足b，c相幅值相等且关于a轴对称；④a相电压相角α0必须为0.由于θ0＝0，如果α0≠0，则由式（10）可知α≠θ，从而就会产生交轴电压分量.

实际设置dq坐标系统的转速和初始位置，条件①，②均成立.但是，在非对称故障情况下，条件③，④均不满足，电压在交直轴均有分量.即便是对称故障或者是非对称故障的正序电压，条件④也不一定满足.由BPA仿真计算获得a相电压相角α0，如图2所示.由此可见，在三相短路故障和单相接地故障下，电压相角均不为0，而且随时间推移还发生一些小的变化.这是由于频率虽然在稳态恒定而且全系统相等，但在动态过程中，各负荷节点频率变化且不一定相同，从而导致相角波动：

综上分析可知，电压相角或交轴分量为0的假设在大多数情况下都不严格成立.故在此假设下，采用单分量实用模型进行参数辨识会产生误差.

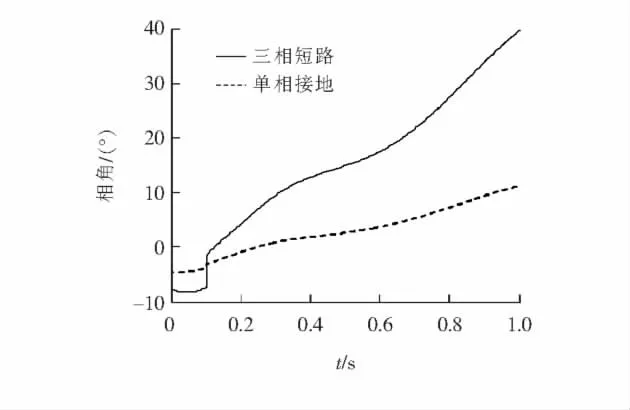
图2 电压相角Figure 2 Voltage phase

3 双分量实用模型的参数辨识

随着测量技术的发展，可以方便地获得负荷母线电压和电流的三相交流值，通过式（10）可变换获得交直轴分量，其中

据此可以采用双分量实用模型（即式（1）～（5））进行参数辨识.

算例为3机9节点系统，如图3所示，其中Bus5为待辨识负荷节点.

图3 3机9节点系统Figure 3 Power system with three generators and nine nodes

1）基于BPA仿真软件，在不同故障情况下仿真得到三相交流数据，录波密度为1kHZ，录波长度为1 001个点，其中，故障前为1个稳态点，故障后为1 000个点.

2）根据三相交流数据，通过Park变换获得交直轴分量.

3）采用2种实用模型分别辨识负荷的重点参数并且进行对比，如表1所示.表1中

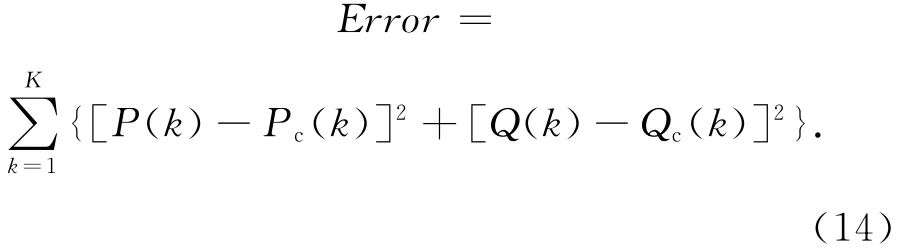
其中 k，K分别为采样点及其总数；下标c代表模型计算值（具体辨识方法参见文献［11］）.

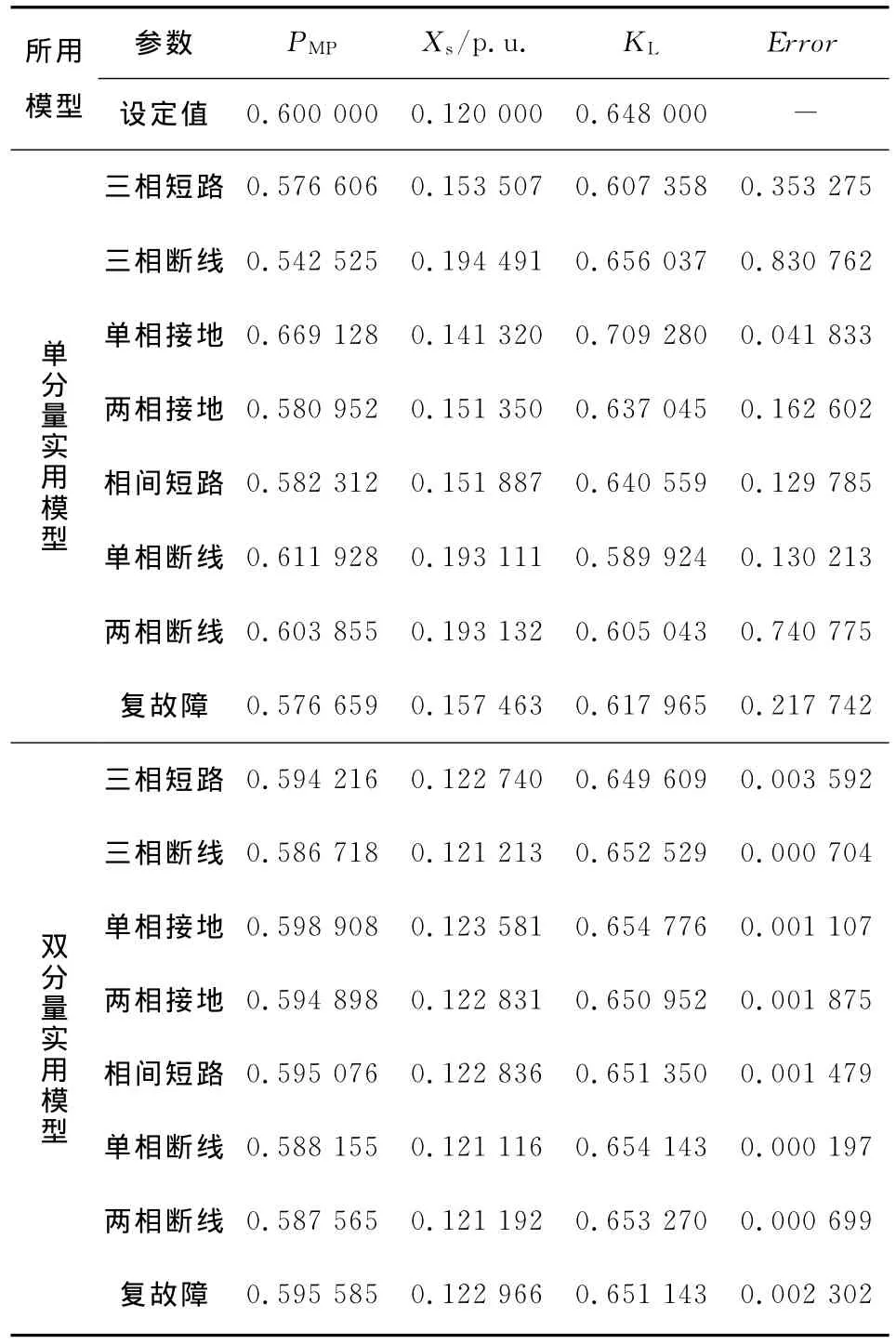
表1 参数辨识结果比较Table 1 Results comparison of the estimated parameters

4）选择3种故障情况下的辨识模型功率曲线与准确功率曲线进行对比.

在故障A（Bus8发生三相短路故障）情况下，电压和功率曲线如图4～6所示.

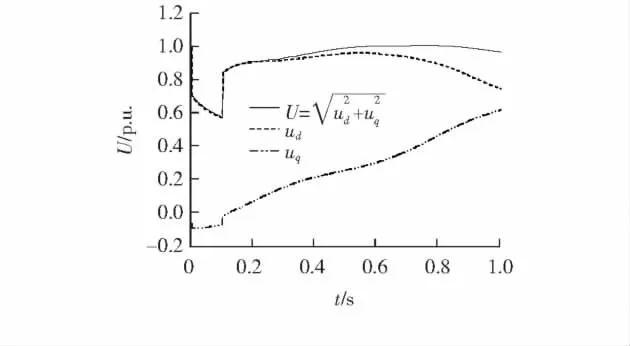
图4 三相短路电压曲线Figure 4 Voltage curve under three－phase short－circuit

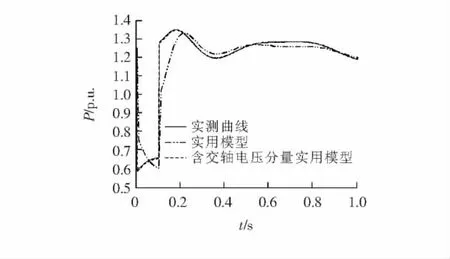
图5 三相短路有功拟合对比曲线Figure 5 Contrast curve of active power under three－phase short－circuit

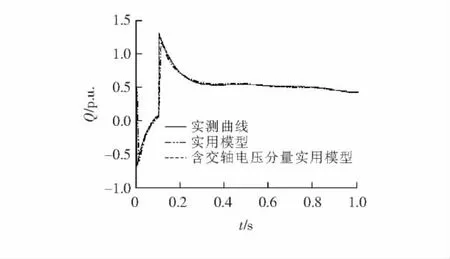
图6 三相短路无功拟合对比曲线Figure 6 Contrast curve of reactive power under three－phase short－circuit

在故障B（Bus8发生复故障）情况下，电压和功率曲线如图7～9所示.

在故障C（Bus5线路上的Bus7侧发生b，c相断线故障）情况下，电压和功率曲线如图10～12所示.

结果表明：①交轴电压分量是一个时变量，在大多数情况下不为0；②采用单分量实用模型，参数辨识结果不平稳而且偏差较大，功率拟合曲线在突变点处误差明显；③采用双分量实用模型，参数辨识结果平稳而且偏差较小，功率拟合曲线拟合很好.

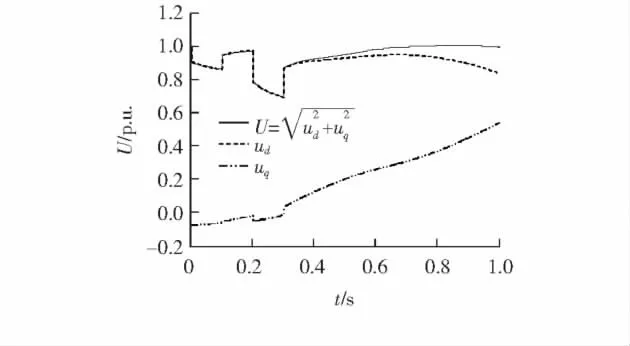
图7 复故障正序电压曲线Figure 7 Positive sequence voltage curve under multiple faults

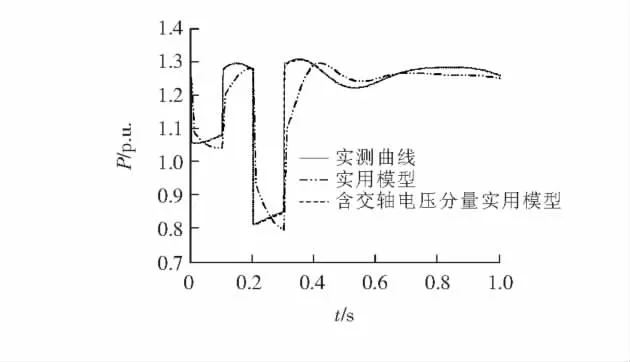
图8 复故障正序有功拟合对比曲线Figure 8 Contrast curve of active power under multiple faults

图9 复故障正序无功拟合对比曲线Figure 9 Contrast curve of reactive power under multiple faults

图10 两相断线正序电压曲线Figure 10 Positive sequence voltage curve under two－phase disconnection

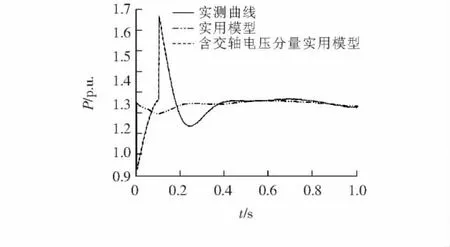
图11 两相断线正序有功拟合对比曲线Figure 11 Contrast curve of positive sequence active power under two－phase disconnection

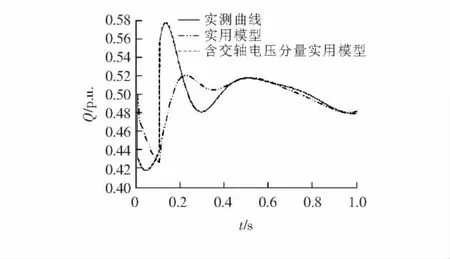
图12 两相断线正序无功拟合对比曲线Figure 12 Contrast curve of positive sequence reactive power under two－phase disconnection

4 结语

笔者分析了忽略电压相角和交轴分量影响的条件，指出应该采用考虑交直轴电压分量的实用模型进行参数辨识.仿真算例的辨识和拟合结果表明，可以获得理想的参数辨识精度和曲线拟合效果.

［1］鞠平，张建勇.电力系统建模基本理论研究综述［J］.电力科学与技术学报，2011，26（1）：4－12.JU Ping，ZHANG Jina－yong.Basic theory reviews of power system modeling［J］.Journal of Electric Power Science and Technology，2011，26（1）：4－12.

［2］Ju P，Handschin E，Karlsson D.Nonlinear dynamic load modelling：model and parameter estimation［J］.IEEE Transations on Power Systems，1996，PWRS－11（4）：1 689－1 697.

［3］Kosterev D N，Taylor C W，Mittelstadt W A.Model validation for the August 10，1996WSCC system outage［J］.IEEE Transations on Power Systems，1999，14（3）：967－979.

［4］张红斌，汤涌，张东霞.不同负荷模型对东北电网送电能力的影响分析［J］.电网技术，2007，31（4）：55－58.ZHANG Hong－bin，TANG Yong，ZHANG Dong－xia.Analysis on effects of different load models on transmitting capacity of Northeast China Power Grid［J］.Power System Technology，2007，31（4）：55－58.

［5］Concordia C，Ihara S.Load representation in power system stability studies［J］.IEEE Transations on Power Apparatus and Systems，1982，101（4）：969－977.

［6］Pereira L，Kosterev D，Mackin P，et al.An interim dynamic induction motor model for stability studies in the WSCC［J］.IEEE Transations on Power Systems，2002，17（4）：1 108－1 115.

［7］张鹏飞，罗承廉，鞠平，等.河南电网送端和受端负荷模型对稳定极限的影响［J］.电网技术，2007，31（6）：51－55.ZHANG Peng－fei，LUO Cheng－lian，JU Ping，et al.Influence of load models in sending and receiving ends of Henan Power Grid on tie－line stability limit of sending end［J］.Power System Technology，2007，31（6）：51－55.

［8］张红斌，汤涌，张东霞，等.负荷建模技术的研究现状与未来发展方向［J］.电网技术，2007，31（4）：6－10.ZHANG Hong－bin，TANG Yong，ZHANG Dong－xia，et al.Present situation and prospect of load modeling technique［J］.Power System Technology，2007，31（4）：6－10.

［9］张景超，鄢安河，张承学，等.电力系统负荷模型研究综述［J］.继电器，2007，35（6）：83－88.ZHANG Jing－chao，YAN An－he，ZHANG Cheng－xue，et al.Summary of load model research in power system［J］.Relay，2007，35（6）：83－88.

［10］汤涌，张红斌，侯俊贤，等.负荷建模的基本原则和方法［J］.电网技术，2007，31（4）：1－5.TANG Yong，ZHANG Hong－bin，HOU Jun－xian，et al.Study on essential principle and methods for load modeling［J］.Power System Technology，2007，31（4）：1－5.

［11］鞠平，马大强.电力系统负荷建模（第2版）［M］.北京：中国电力出版社，2008.

［12］曹一家，李大虎.基于广域测量系统的大区域电网负荷建模的研究［J］.电力科学与技术学报，2007，22（2）：1－7.CAO Yi－jia，LI Da－hu.Study on large scale grid load modeling based on wide area measurement system［J］.Journal of Electric Power Science and Technology，2007，22（2）：1－7.

［13］张红斌，汤涌，张东霞，等.基于总体测辨法的电力负荷建模系统［J］.电网技术，2007，31（4）：32－35.ZHANG Hong－bin，TANG Yong，ZHANG Dong－xia，et al.Load modeling system founded on measurement based method［J］.Power System Technology，2007，31（4）：32－35.

［14］邵正炎，史可琴，鞠平，等.间接与直接考虑配电网的2种负荷模型对比研究［J］.中国电力，2008，41（3）：29－31.SHAO Zheng－yan，SHI Ke－qin，JU Ping，et al.Comparison between the load models with considering distribution network directly or indirectly［J］.Electric Power，2008，41（3）：29－31.

［15］周海强，茆超，蔡敏，等.考虑配电网络的综合负荷模型的可辨识性分析［J］.电力系统自动化，2008，32（16）：16－19.ZHOU Hai－qiang，MAO Chao，CAI Min，et al.Identifiability analysis of a synthesis load model with considering distribution network［J］.Automation of Electric Power Systems，2008，32（16）：16－19.

［16］汤涌，张红斌，侯俊贤，等.考虑配电网络的综合负荷模型［J］.电网技术，2007，31（5）：34－38.TANG Yong，ZHANG Hong－bin，HOU Jun－xian，et al.A synthesis load model with distribution network［J］.Power System Technology，2007，31（5）：34－38.

［17］施雄华，陈根军，鞠平，等.一种新的广义电力负荷模型及其工程应用［J］.电力科学与技术学报，2011，26（2）：44－48.SHI Xiong－hua，CHEN Gen－jun，JU Ping，et al.A new generalized power system load model and its application［J］.Journal of Electric Power Science and Technology，2011，26（2）：44－48.

［18］Ma Jin，He Renmu，Hill D J.Load modeling by finding support vectors of load data from field measurements［J］.IEEE Transations on Power Systems，2006，21（2）：726－735.

［19］He Renmu，Ma Jin，Hill D J.Composite load modeling via measurement approach［J］.IEEE Transations on Power Systems，2006，21（2）：663－672.

［20］倪以信，陈寿孙，张宝霖.动态电力系统的理论与分析［M］.北京：清华大学出版社，2002.

［21］Kundur P.Power system stability and control［M］.New York：McGrawHill，1994.

［22］鞠平.电力系统建模理论与方法［M］.北京：科学出版社，2010.

［23］沈善德.电力系统辨识［M］.北京：清华大学出版社，1988.