挂舵臂弹性支撑的舵-舵杆系统直接计算分析

徐蓉奚君

（上海船舶研究设计院，上海 201203）

0 前言

大型船舶大多采用的半悬挂舵由于受到挂舵臂的影响，受力情况比较复杂。一般根据船级社规范中的简化公式计算，不考虑挂舵臂的弹性支撑，往往使构件尺寸尤其是舵销直径的计算结果偏大，带来不必要的重量，影响船舶的经济性。故有必要在舵－舵杆系统设计过程中考虑挂舵臂的弹性支撑，并引入梁的弯曲理论进行直接计算，建立舵杆的力学模型，对舵－舵杆系统进行受力分析，以确定在舵－舵杆系统设计中关键的参数，即挂舵臂在舵销处实际的支撑力B1。

1 挂舵臂弹性支撑的舵-舵杆系统力学模型分析

图1是挂舵臂弹性支撑的舵－舵杆系统的结构示意图，以1700 TEU集装箱船的半悬挂舵为例，其舵叶外形尺寸如图2所示，CR=2196.017 kN。根据德国船级社（GL）规范规定，在初步确定构件尺寸时，可忽略不计挂舵臂的柔性，支撑力B1按下述式确定：

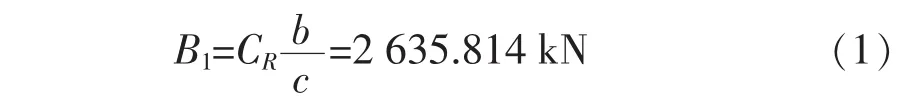
式中：B1——支承力，N；

CR——舵力，N；

b——颈部轴承距舵面积重心的距离，mm；

c——颈部轴承距舵销中心的距，mm

假设舵销的屈服极限σeH=280 N/mm2，那么根据GL规范，按照以上支撑力B1可得舵销直径的最小值：

式中：kr——材料系数；

ReH——材料的屈服极限，N/mm2

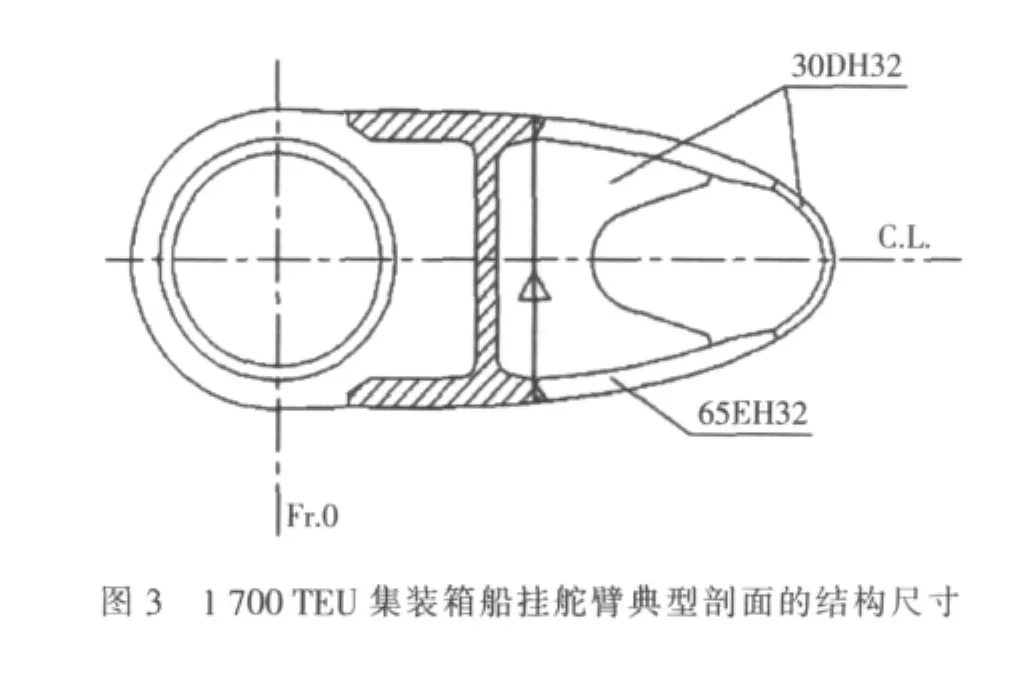
上述支撑力B1除用来确定舵销直径以外，还可用以校核挂舵臂的构件尺寸是否满足规范要求，得到初步的挂舵臂设计尺寸，如截面面积、板厚等。如图3所示为1700 TEU集装箱船挂舵臂典型剖面的结构尺寸。

由于挂舵臂本身的柔性对舵-舵杆系统起到弹性支撑的作用，使实际的支撑力B1比按上式计算得到的结果小。在GL规范第13节中提到，B1是按第14节C.3确定的支撑力，而根据第14节C.3内容所述，B1应是考虑了挂舵臂弹性支撑后确定的支撑力。

为确定1700 TEU集装箱船挂舵臂在舵销处实际的支撑力B1，引入梁的弯曲理论，得到如图4所示舵-舵杆系统的力学模型。其中l10=4550 mm，l20=3400 mm，l30=300 mm，l40=2400 mm。

另外，根据GL规范第14节C.3的规定，模型中作用于梁上的均布载荷PR10、PR20和挂舵臂的弹性支撑系数Z按下述确定。

式中：PR10、PR20——舵叶的载荷分布，kN/m；

CR1、CR2——舵面积的压力分布，N；

l10——舵的几何尺寸，mm；

Z——挂舵臂的弹性支撑系数，kN/m；

fb——在支承中心处作用1 kN的单位力时产生的挂舵臂的单位位移，m/kN；

ft——因扭转产生的单位位移，m/kN

建立上述简支梁力学模型后，从力学手册上可查到转角和挠度，从而建立理论计算方程式得到B1值。但该过程比较繁杂和冗长，故笔者建议采用DNV 3D－beam软件对挂舵臂弹性支撑的舵－舵杆系统进行受力计算和分析，不仅结果可靠，而且在很大程度上简化了计算过程，提高了设计效率。

2 采用3D-BEAM软件对上述力学模型的计算分析

对于梁系的受力分析来说，计算软件DNV 3DBEAM方便快捷，易于掌握，只要保证计算模型的简化合理且趋于保守，结果能够避免较大误差。根据上述对舵－舵杆系统的力学模型分析结果，在DNV 3D－BEAM软件中建立简支梁的力学模型，如图5所示。

为了简化舵杆结构的受力计算过程，不考虑舵杆在上、下舵承处的截面变化，以及某些位置由舵叶结构替代舵杆的受力情况。在模型中采用平均直径为475 mm的实心圆柱型材模拟舵－舵杆系统。模型中梁的属性、施加的边界条件及载荷大小如表1～3所示，颈部轴承和上轴承处施加简支的边界条件，挂舵臂支撑处采用弹性支撑，舵叶下边为自由端。

表1 梁的属性

表2 梁的边界条件

表3 梁的载荷

模型的应力结果如表4所示，其中最大合成应力σNY=277 N/mm2，小于舵杆的屈服极限σeH=280 N/mm2，可见舵杆满足强度要求。如图6、图7所示分别为剪力和弯矩分布图。

表4 模型的应力

模型中各约束端的变形及支反力结果如表5所示，可得支撑力B1=2054.042 N，则舵销直径的最小值为：

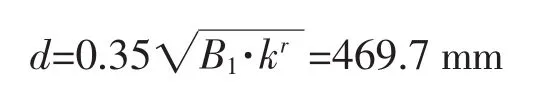
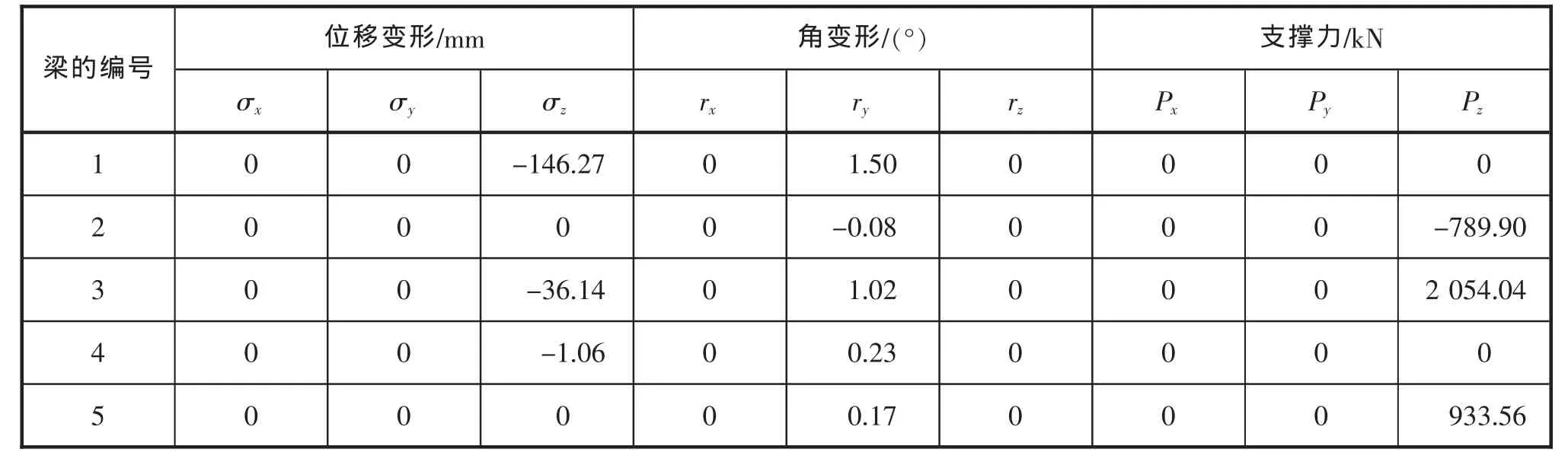
表5 变形及支反力

3 结语

与用规范计算的支撑力B1得到的舵销直径相比，根据直接计算的支撑力B1得到的舵销直径减小了12%。由此可见考虑挂舵臂对舵-舵杆系统的弹性支撑后，对减小舵销的直径十分有利。

不同船级社规范中规定的舵-舵杆系统的设计简化公式有较大差别，以至结果的差异也很大。如果对舵-舵杆系统采用直接计算方法进行分析，则能在较大程度上统一舵-舵杆系统的设计参数，避免同型船因入级不同而带来设计参数的不统一。