分数(g，f，n'，m)－临界消去图的2个充分条件

高炜

(云南师范大学信息学院，云南昆明650092)

分数(g，f，n'，m)－临界消去图的2个充分条件

高炜

(云南师范大学信息学院，云南昆明650092)

设G是一个图，若去掉G中的任意n'个顶点的剩余子图仍是分数(g，f，m)-消去图，则称G是一个分数(g，f，n'，m)-临界消去图.从独立数和度条件2个角度出发，分别给出了图G是分数(g，f，n'，m)-临界消去图的2个充分条件.

图;分数临界图;分数临界消去图

1 预备知识

本文只考虑无向、简单、有限图.文中涉及的符号和标记若没有特别说明，则与文献［1］一致.设G是一个图，具有顶点集V(G)和边集E(G).顶点x的度和最小度分别记为dG(x)和δ(G).令S和T是V(G)的任意2个不相交的子集.EG(S，T)表示一个顶点在S中而另外一个顶点在T中的G的边集合.记eG(S，T)= EG(S，T)，dG-S(T)=dG(T)-eG(S，T)且dG-T(S)=dG(S)-eG(S，T).设g和f分别是定义在V(G)上的2个整数值函数且对每个x∈V(G)有g(x)≤f(x).分数(g，f)-示性函数h是一个函数分配给图G的每一条边一个［0，1］之间的数，使得对每一个点x∈V(G)有g(x)≤dGh(x)≤f(x)，其中dGh(x)=∑e∈Exh(e)是点x∈V(G)的分数度，且Ex={e:e=xy∈E(G)}.设h是图G的分数(g，f)-示性函数.令Eh= {e:e∈E(G)，h(e)≠0}.若Gh是G的支撑子图使得E(Gh)=Eh，则Gh称为G的分数(g，f)-因子.若去掉G中的任意n'个顶点的剩余子图仍有分数(g，f)-因子，则称G为分数(g，f，n')-临界图.若去掉G中的任意m条边的剩余子图仍有分数(g，f)-因子，则称G为分数(g，f，m)-消去图.一个图G称为分数(g，f，n'，m) -临界消去图，若去掉G中的任意n'个顶点的剩余子图仍是分数(g，f，m)-消去图.

文献［2］给出了一个图有分数f-因子的独立数和最小度条件.

定理1［2］设G是一个连通图，a≤b为非负整数，f(x)是定义在V(G)上的整数值函数使得对于所有的x∈V(G)都有a≤f(x)≤b.如果δ(G)≥b，独立数，则G有分数f-因子.

文献［3］给出了图有分数(g，f)-因子的一个度条件.

定理2［3］设G是1个图.如果对于任意的1对顶点v，w∈V(G)都有

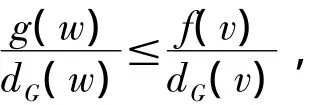
则G有分数(g，f)-因子.

文献［4］将上述2个结论推广到分数(g，f，n')-临界图的情形，得到了如下结论.

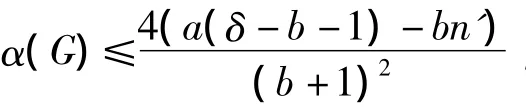
定理4［4］设G是1个图，a，b和n'是非负整数，a≤b.设g(x)和f(x)是定义在V(G)上的非负整值函数且满足对任意的x∈V(G)都有a≤g(x)≤f(x)≤b.若对于任意的1对顶点v，w∈V(G)，都有

则G是分数(g，f，n')-临界图.

本文将文献［4］中结果推广到分数(g，f，n'，m)-临界消去图的情形，证明了如下2个结论.

定理6设G是1个图，a，b，n'和m是非负整数，a≤b.设g(x)和f(x)是定义在V(G)上的非负整值函数且满足对任意的x∈V(G)都有a≤g(x)≤f(x)≤b.若对于任意的1对顶点v，w∈V(G)，都有则G是分数(g，f，n'，m)-临界消去图.

可见，在定理5和定理6中分别令m=0，即得定理3和定理4.此外，在定理5中，如果对于任意的x∈V(G)都有f(x)=g(x)，则可得如下推论.

在推论1中，如果n'=0，则可得如下推论.

在定理6中，如果对于任意的x∈V(G)都有f(x)=g(x)，则可得如下推论.

推论3设G是1个图，a，b，n'和m是非负整数，a≤b.设f(x)是定义在V(G)上的非负整值函数且满足对任意的x∈V(G)都有a≤f(x)≤b.若对于任意的1对顶点v，w∈V(G)，都有

则G是分数(f，n'，m)-临界消去图.

在推论3中，如果n'=0，则可得如下推论.

推论4设G是1个图，a≤b是非负整数，m≥0是整数.设f(x)是定义在V(G)上的非负整值函数且满足对任意的x∈V(G)都有a≤f(x)≤b.若对于任意的1对顶点v，w∈V(G)，都有

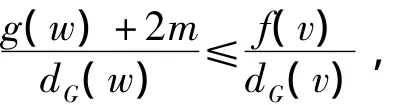
则G是分数(f，m)-消去图.

为证明定理5和定理6，我们需要引入引理1作为己知结论.

引理1［5］设G是1个图，g，f是定义在顶点集上的2个非负整值函数满足对所有x∈V(G)有g(x)≤f(x).设n'，m为非负整数.G是分数(g，f，n'，m)-临界消去图当且仅当

2 主要结论的证明

下面我们给出2个定理的详细证明，其证明思路主要参考文献［4］.

定理5的证明设G满足定理5的条件但不是分数(g，f，n'，m)-临界消去图.显然，T≠∅，否则(1)成立.由引理1知，存在不交的S，T满足

其中S≥n'.选择S，T使T最小.从而，dG-S(T)≤b-1对所有x∈T成立.否则，若存在x∈T使得dG-S(x)≥b，则子集S，T{x}同样满足(2).这与S，T的选取矛盾.

设d=min{ dG-S(x)x∈T}，则

由于T≠∅，我们可构造T的序列x1，x2，…，xk如下:取x1∈T使得x1是G［T］中度最小的顶点.设N1=NG［x1］∩T且T1=T.对于i≥2，如果∪＜iNj≠φ，设Ti=T-∪＜iNj.取xi∈Ti使得xi是G［Ti］中度最小的顶点，设Ni=NG［xi］∩Ti.继续这个过程直到对某个i，使得Ti=∅，记i=k+1.从而可知x1，x2，…，xk是G的独立集.因为T≠∅，所以k≥1.

设Ni=ni.由Ni的定义，可以得到下列性质.

结合(2)，(5)，(7)可得

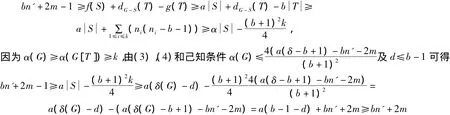
矛盾.从而结论成立.

定理6的证明设G满足定理6的条件但不是分数(g，f，n'，m)-临界消去图.显然，T≠∅.由引理1知，存在不交的S，T满足

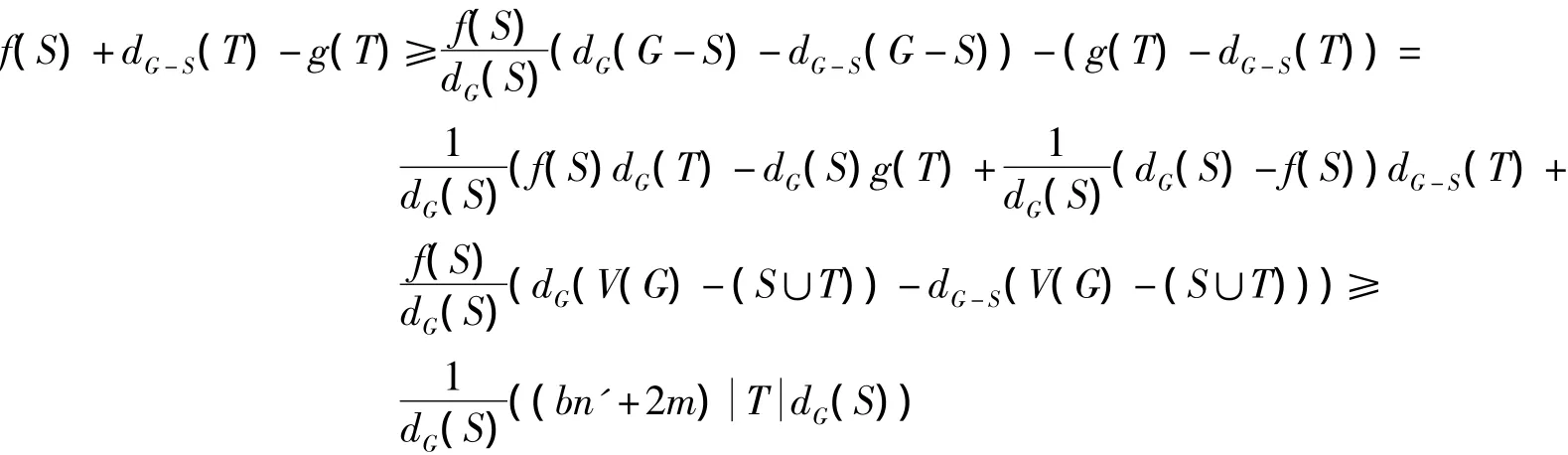
由如上不等式可得矛盾.从而结论成立.

其中Kib是有b个顶点的完全图(1≤i≤k+1).

因此可知G不是分数(g，f，n'，m)-临界消去图.

［1］BONDY J A，MUTRY U S R.Graph theory［M］.Berlin:Springer-Verlag，2008.

［2］CAI J，LIU G，Degree and stability number condition for the existence of connected factors ingraphs［J］.J Appl Math Comput，2009，29:349-356.

［3］LIU G，ZHANG L.Maximum fractional(0，f)-factors of graphs［J］.Mathematica Applicata，2000，13:31-35.

［4］刘红霞.图参数与图的因子［D］.济南:山东大学，2010.

［5］高炜.关于分数消去图的若干结果［D］.苏州:苏州大学，2012.

(责任编辑万志琼)

Two Sufficient Conditions for(g，f，n'，m)Critical Deleted Graph

GAO Wei
(School of Information，Yunnan Normal University，Kunming 650092，China)

Supposing graph G is a fractional(g，f，n'，m)critical deleted graph，if after deleting any n'vertices of G，the remaining graph is a fractional(g，f，m)deleted graph.Taking the independent number and degree condition into consideration，the paper gives two sufficient conditions for the fractional(g，f，n'，m)critical deleted graph.

graph;fractional critical graph;fractional critical deleted graph

O 157

A

1672-8513(2012)04-0273-04

10.3969/j.issn.1672-8513.2012.04.011

2011-12-22.

国家自然科学基金(11071223).

高炜(1981-)，男，博士，讲师.主要研究方向:图论、统计学习理论.