基于红外测温的异步电机轴承故障诊断

孙斌， 王艳武， 杨立

(1．武汉理工大学能源与动力学院，湖北武汉 430063;2.92601部队，广东湛江 524005;3．海军工程大学船舶与动力学院，湖北 武汉 430033)

0 引言

中小型感应电动机以其结构简单、运行可靠、效率较高、制造容易、成本较低等优点在工农业生产中广泛应用。特别是在海军舰船上，各类泵、风机、锚机等设备均采用异步电机作为原动机，因此电机运行状态直接关系到舰船战斗力，对电机运行状态进行实时监测就具有重要的军事意义。而对舰船上各类电机而言，运行实践表明异步电机轴承故障是电机的主要故障之一，约占电机总故障的30% ～40%［1］，因此为保证设备安全可靠运行和舰船战斗力，对异步电机轴承故障进行早期监测与诊断，具有重要的军事和经济价值。

目前对电机轴承的诊断，应用较多的有定子电流检测法［2－5］和振动检测法［6－10］。但是这两种检测方法对于海军舰船，特别是执行远航任务的舰船来说，进行舰员级的实时监测存在较大困难。而红外监测由于仪器操作简便，结果显示直观，使用最为熟练和频繁，但是对电机轴承状态的判断缺乏相应的理论依据。针对这一问题，本文在综合分析电机轴承滚珠破损、保持架断裂、润滑不良、滑油失效等常见故障的热特征后发现，当电机轴承出现故障后，其表现出来的一个重要特征就是轴承安装部位温度升高。但是目前对船用中小型异步电机温度场的研究相对较少，哈尔滨理工大学靳廷船［11］、海军工程大学王艳武［12］等人分别对感应电机定子和转子温度场及转子热应力场的分布规律进行了研究，但是对于电机轴承运行性能不同时电机转子温度场的变化情况则缺乏相应的研究。本文根据舰船电机实际特点，分别对异步电机转子温度场开展理论和实验研究，进一步获取电机轴承故障时的温度场特征，为电机轴承早期故障的红外诊断提供理论支持。

1 电机轴承故障时转子温度场仿真研究

1.1 电机转子三维模型建立

本文研究以Y100L－2型电机为对象。根据研究的目的，取转子、电机轴承、端盖为整个求解区域，端盖外部风扇在实际应用中被风扇罩盖住，所以建立模型不考虑风扇，而是直接利用轴取代，图1为在ANSYS下建立的电机输出端轴承故障时转子三维几何模型;图2为模型中间部位横截面示意图。

根据结构的对称性和电机导热特点，作如下假设:

1)电机转子端部两侧的空腔中空气温度均匀;

2)轴承产生的热量均匀分布在整个轴承体，取轴承为相对静止;

3)轴承、转轴和轴承座过盈配合，接触良好;

4)电机在圆周方向的冷却条件相同;

5)在一定工况下，电机轴承的摩擦损耗，即模型轴承部分的内热源越大，表示轴承状态越差，故障程度越严重。

图1 转子三维模型图Fig．1 3D model of rotor

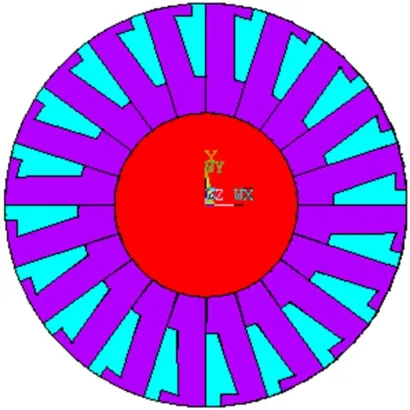
图2 转子模型横截面示意图Fig．2 Cross section of model

根据以上假设，针对计算区域建立三维稳态传热数学模型［13］为

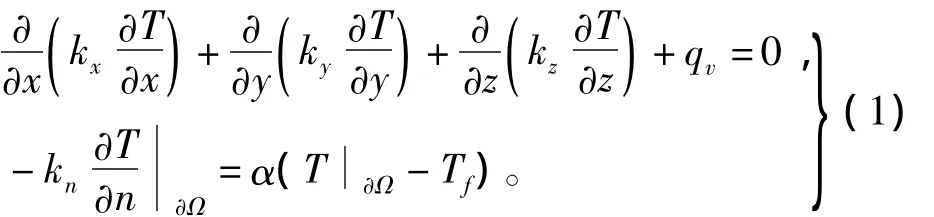
式中:kx、ky、kz、kn分别为导热介质在x、y、z和边界法线方向的导热系数;qv为单位介质体积发热率;α为对流换热系数;Ω为计算区域;∂Ω为计算区域边界;T为模型计算区域温度;Tf为冷却介质温度。

1.2 边界条件

电机本身是一个有热源的传热体，其热量传递过程，主要是热传导和对流换热过程，即导热和对流换热的综合过程。由传热学基础知识可知，上述过程与介质的导热系数和表面对流换热系数直接有关，本文对这些系数的确定主要是依据相关经验公式结合实验测量获得［14－15］。对于模型内热源的确定，主要是利用试验测量结合研究电机型号查阅相关资料获得。对于中小型异步电机，其轴承基本上是滚动轴承，滚动轴承的摩擦损耗可用经验公式进行计算［15］，即

式中:n为电机转速，r/min;mb为摩擦力矩，N·m。

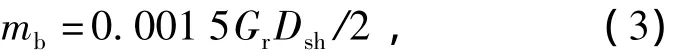
式中:Gr为转子重量，kg;Dsh为转轴直径，m。

1.3 温度场仿真分析

根据假设及边界条件，对电机在空载运行，电机轴承发生故障时的三维温度场进行仿真研究。在电机正常运行时，电机轴承的损耗可以按式(2)和式(3)进行计算;当输出端轴承出现故障时，随着故障严重程度的增加，轴承损耗也增加。根据故障程度的不同，假设轴承损耗是电机额定输出功率的0.5%和1%，并以此为故障轴承内热源进行计算。图3～图5分别为电机正常运行、电机输出端轴承损耗为电机额定输出功率的0.5%、输出端轴承损耗为电机额定输出功率的1%时转子三维温度场分布云图。

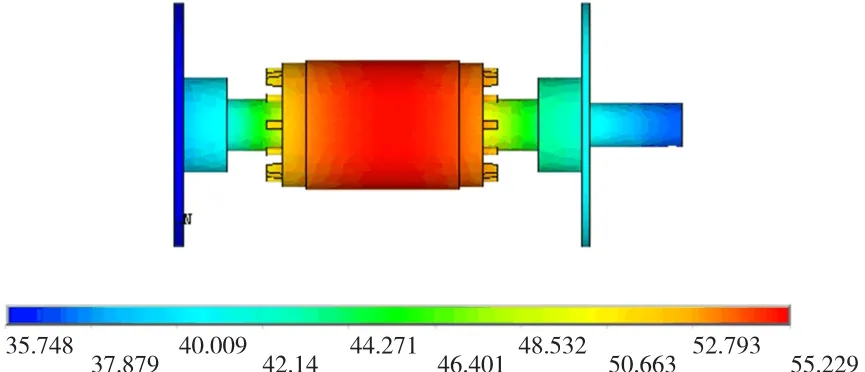
图3 正常运行转子三维温度场分布云图Fig．3 3D thermal field of rotor without fault

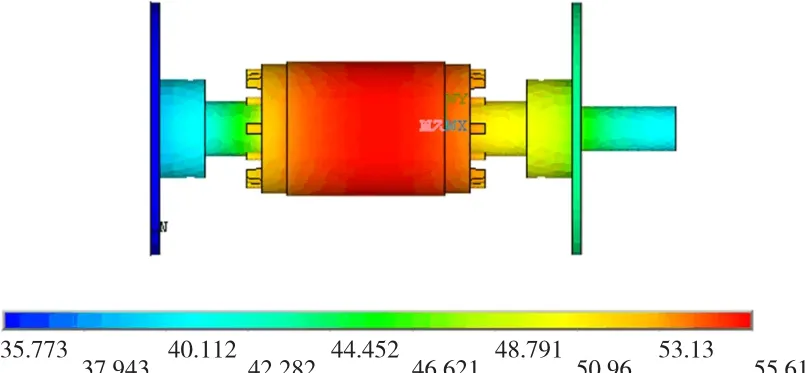
图4 输出端轴承损耗为额定输出功率0.5%转子三维温度场分布云图Fig．4 3D thermal field of rotor with 0.5%rated load losses in bearing

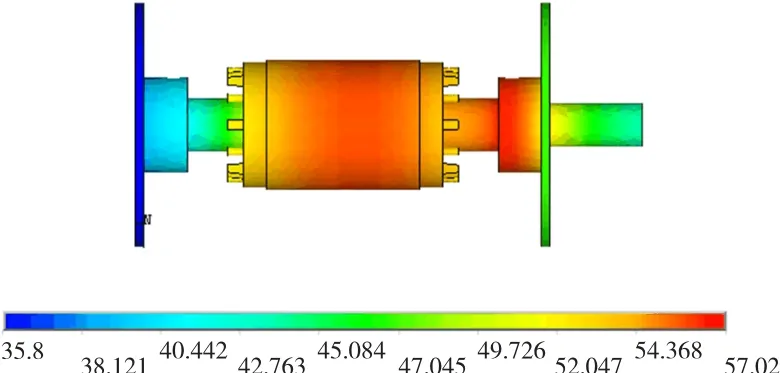
图5 输出端轴承损耗为额定输出功率1%转子三维温度场分布云图Fig．5 3D thermal field of rotor with 1%rated load losses in bearing

从仿真计算结果来看，随着轴承状态的恶化，轴承产生热量增加，导致轴承部位温度升高，但是对整个转子部分的温升影响不大。在轴承损耗为电机额定输出功率的0.5%时，整个模型温度最高值比正常时最高温度升高约0.4℃;当轴承损耗为额定输出功率的1%时，最高温度比正常时高出约1.8℃;而轴承在三种状态下，转子部分最低温度变化基本上可以忽略，因此从温度值的变化来看，整个转子部分温升并不很明显。但是随着轴承状态的恶化，其损耗的增加，转子部分最高温度的位置发生了变化，在正常运行时，整个模型最高温度点出现在转子铁心部分，而随着轴承状态的恶化，其损耗的进一步加大，模型最高温度点则出现在故障轴承处。同时随着输出端轴承的恶化，输出轴温度整体升高，但是风扇端转轴温度变化不大，而整个模型的最低温度位置也没有发生改变，仍然出现在风扇端端盖。

图6～图8为轴承状态改变时，输出端端盖表面温度场分布云图。从计算结果来分析，端盖表面温度从中心沿径向向外逐步降低。随着轴承状态的恶化，端盖表面温度整体升高，端盖部分的温差加大，这也说明轴承状态的好坏对端盖表面的温度场影响较大，可以通过监测端盖表面温度场的变化，获取轴承状态信息。

图6 正常运行输出端端盖温度场分布云图Fig．6 Surface thermal field of motor cover without fault

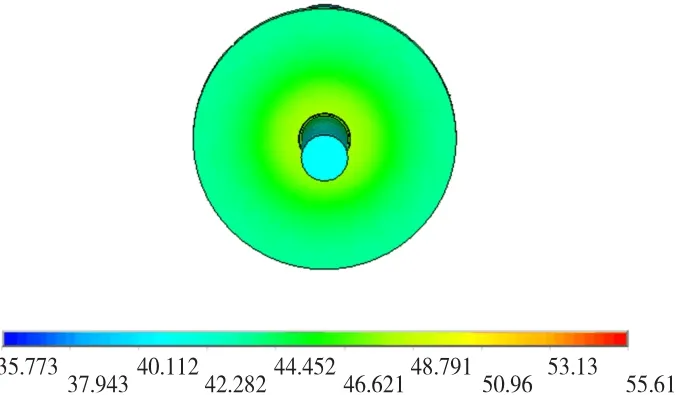
图7 轴承损耗为额定输出功率0.5%端盖温度场分布云图Fig．7 Surface thermal field of motor cover with 0.5%rated load losses in bearing

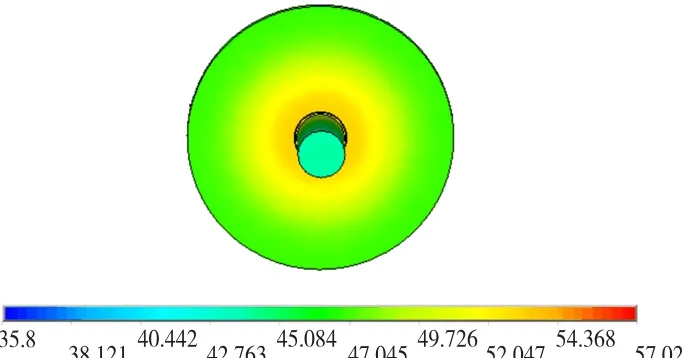
图8 轴承损耗为额定输出功率1%端盖温度场分布云图Fig．8 Surface thermal field of motor cover with 1%rated load losses in bearing

图9所示为空载时电机输出端端盖外表面从内到外沿径向的温度分布曲线。图中显示，当轴承损耗为额定输出功率的1%时，端盖外表面温度最高，而当损耗为0.5%时次之，轴承正常时温度最低。3种状态下，均是端盖靠轴承安装位置的部分温度最高，沿径向逐步降低。随着轴承状态的恶化，端盖表面温升增加的同时，温差也进一步加大。3种状态下，端盖部分最高温度分别为 42.35、47.85和53.74℃，温升分别为13.18、18.68和24.57℃，即当轴承损耗达电机额定输出功率的1%时，端盖部分最大温升几乎是正常时的2倍，即使损耗为额定输出功率的0.5%，最大温升也几乎是正常时的1.5倍，这说明轴承状态的变化，直接影响到端盖部分的温升，因此通过端盖部分温度的变化，即可判断轴承状态的变化。而3种状态下，端盖部分的最大温差分别为1.78、4.04和6.46℃，即随着轴承状态的恶化，损耗的增加，电机端盖温升增加的同时，端盖部分温差也增加。

图9 输出端端盖外表面径向温度分布曲线Fig．9 Temperature curves of motor cover in radial

2 电机轴承故障实验测量结果分析

实验以Y100L－2型电机为研究对象，输出端轴承故障。图10为润滑良好，无故障轴承。图11为保持架及滚珠被破坏的轴承。实验时首先利用红外热像仪测量电机空载状态下轴承工作正常时输出端端盖的温度分布，如图12所示;图13为输出端轴承保持架和滚珠损坏时，电机空载时的输出端端盖红外热图。

图10 完好轴承Fig．10 Bearing without faults

图11 故障轴承Fig．11 Bearing with faults

图12 轴承正常时输出端端盖红外热图Fig．12 Infrared image of cover without faults

图13 轴承故障时输出端端盖红外热图Fig．13 Infrared image of cover with bearing faults

分析两种状态下测量的轴承红外热图，发现在轴承故障时，端盖中心部位轴承安装位置温度与周围边界轮廓清楚，而轴承正常时则相对模糊些，说明轴承故障时对端盖温度场分布还是存在一定影响的。在实验测量时，环境温度基本一致，但是端盖表面最高温度发生变化。测量区域中最高温度由轴承良好时的42.0℃升高到轴承故障时的46.4℃，说明轴承故障对端盖温度最高温升有影响，这一点与理论仿真结果相同。

图14为实验测量的在轴承正常和故障状态下的端盖表面径向温度分布曲线。从温度分布曲线来看，与图9中理论仿真的端盖表面温度分布曲线的分布规律基本一致，即端盖表面从中心向边缘沿径向温度是逐步降低的。从测量结果来看，轴承正常时最高温度为39.5℃，温升仅仅为10℃左右，端盖表面温差为3.9℃;轴承故障时端盖表面最高温度为43.4℃，比环境温度高14℃，此时端盖温度明显高于轴承正常时的温度;轴承故障时端盖表面温差为6.8℃，比轴承正常时高出近3℃，说明轴承故障时导致端盖温升增加的同时也导致端盖表面温差的增加，这一结论与理论仿真结论也一致。同时从实验测量的热图和数据来看，端盖表面中心位置，即轴承座位置，端盖表面温度明显高于周围，其沿径向向外温度变化缓慢，这一点理论计算温度分布曲线也得到体现。但是继续沿径向向外，端盖表面温度则降低很快，说明端盖表面温度分布受轴承的影响很大，因此可以通过对端盖表面温度分布规律结合温差来对轴承状态进行判断。

图14 空载实验测量端盖表面径向温度分布曲线Fig．14 Temperature curves of cover in radial by experiment measured on unloaded motor

图15、图16为另一台轴承外圈存在故障电机在负荷发生变化时测量的电机端盖表面红外热图。从测量的结果来分析，当轴承故障程度不发生变化，电机负荷发生变化时，电机端盖表面温度分布规律几乎没有变化。这说明电机负荷的变化，对端盖温度场的分布规律影响不大，仅仅是温升增加。图17为两种负荷下测量的端盖表面径向温度分布曲线。从测量结果来看，在电流为4.75 A时，端盖表面温差为2.4℃，而负载增加，电流为6.2 A时，温差为2.7℃。即电机负荷增加时，端盖表面温升和温差均增加，但是端盖表面温度分布规律基本不变。

图15 电压350 V电流4．75 A端盖热图Fig．15 Infrared image of cover when U=350 V and I=4．75 A

图16 电压350 V电流6．2 A端盖热图Fig．16 Infrared image of cover when U=350 V and I=6．2 A

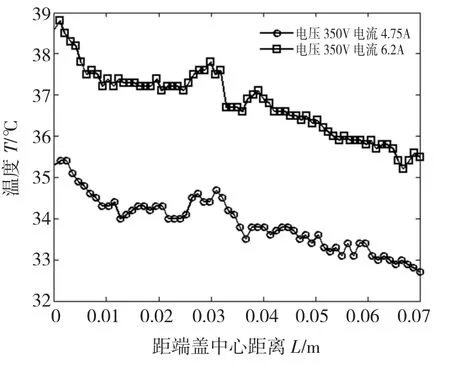
图17 负载实验测量端盖表面径向温度分布曲线Fig．17 Temperature curves of cover in radial by experiment measured on loaded motor

3 结语

通过对轴承处于不同故障程度的电机转子三维温度场的仿真研究及电机轴承故障的实验分析，发现电机端盖温度分布，不论轴承是否有故障，均是沿径向从内到外温度逐步降低，在端盖轴承座正对部位，温度变化缓慢，但是从轴承外径继续向外，端盖温度下降迅速;负荷条件相同时，轴承损坏越严重，端盖表面温升越大，因此通过同一种负荷条件下端盖表面温升的变化可以对轴承状态进行初步判断;电机端盖表面的绝对温升随负荷增加而升高，因此不能仅仅凭借端盖表面温升来对相应轴承状态进行判断;电机负荷的变化虽然对端盖温升影响很大，但是对端盖温度场的分布规律影响却很小，基本可以忽略;利用红外热像仪测量电机端盖表面温度场分布规律，可以对电机轴承状态进行实时判断。为了进一步对电机轴承故障进行红外诊断，需要对电机轴承各类故障的发热机理进行研究。

［1］马宏忠．电机状态监测与故障诊断［M］．北京:机械工业出版社，2008:1－835．

［2］SCHOEN R R，HABETLER T G，KAMRAN F，et al．Motor bearing damage detection using stator current monitoring［J］．IEEE Transactions on Industry Applications，1995，31(6):1274－1279．

［3］BLODT M，GRANJON P，RAISON B，et al．Models for bearing damage detection in induction motors using stator current monitoring［J］．IEEE Transactions on Industrial Electronics，2008，55(4):1813－1822．

［4］ZAREI J，POSHTAN J．An advanced Park’s vectors approach for bearing fault detection［J］．Tribology International，2009，42:213－219．

［5］侯新国，吴正国，夏立，等．基于Park矢量模信号小波分解的感应电机轴承故障诊断方法［J］．中国电机工程学报，2005，25(14):115－119．

HOU Xinguo，WU Zhengguo，XIA Li，et al．Bearing fault diagnosis method of induction motor via wavelet decomposition of Park’s vector modulus signal［J］．Proceedings of the CSEE，2005，25(14):115－119．

［6］夏立，费奇．感应电机轴承故障检测方法研究［J］．振动、测试与诊断，2005，25(4):307 －310．

XIA Li，FEI Qi．Fault detection of induction motor bearing［J］．Journal of Vibration，Measurement＆ Diagnosis，2005，25(4):307－310．

［7］李运红，张湧涛，裴未迟．基于小波包－Elman神经网络的电机轴承故障诊断［J］．河北理工大学学报:自然科学版，2008，30(4):81－85．

LI Yunhong，ZHANG Yongtao，PEI Weichi．Fault diagnosis of the motor bearing based on the wavelet package-Elman neural network［J］．Journal of Hebei Polytechnic University:Natural Science Edition，2008，30(4):81－85．

［8］RILEY C M，LIN B K，HABETLER T G，et al．A method for senseless on-line vibration monitoring of induction machines［J］．IEEE Transactions on Industry Applications，1998，34(6):1240－1245．

［9］LI Bo，CHOW Moyuen，TIPSUWAN Yodyium，et al．Neural-network-based motor rolling bearing fault diagnosis［J］．IEEE Transactions on Industrial Electronics，2000，47(5):1060 －1069．

［10］罗忠辉，薛晓宁，王筱珍，等．小波变换及经验模式分解方法在电机轴承早期故障诊断中的应用［J］．中国电机工程学报，2005，25(14):125 －129．

LUO Zhonghui，XUE Xiaoning，WANG Xiaozhen，et al．Study on the method of incipient motor bearing fault diagnosis based on wavelet transform and EMD［J］．Proceedings of the CSEE，2005，25(14):125－129．

［11］靳廷船，李伟力，李守法．感应电机定子温度场的数值计算［J］．电机与控制学报，2006，10(5):492－497．

JIN Tingchuan，LI Weili，LI Shoufa．Numerical calculation and analysis of stator thermal field in an induction machine［J］．Electric Machines and Control，2006，10(5):492 －497．

［12］王艳武，杨立，陈翾，等．异步电机转子三维温度场及热应力场研究［J］．电机与控制学报，2010，14(6):27－32．

WANG Yanwu，YANG Li，CHEN Xuan，et al．Study on 3D thermal field and thermal stress field of the induction motor rotor［J］．Electric Machines and Control，2010，14(6):27 －32．

［13］俞昌铭．热传导及数值分析［M］．北京:清华大学出版社，1982:256－560．

［14］魏永田，孟大伟，温嘉斌．电机内热交换［M］．北京:机械工业出版社，1998:1－357．

［15］黄国治，傅丰礼．Y2系列三相异步电动机技术手册［M］．北京:机械工业出版社，2004:131－154．