试验研究VFTO作用下层式绕组暂态特性
郑殿春, 翟修全, 赵大伟, 吕树明
(哈尔滨理工大学电气与电子工程学院,黑龙江哈尔滨 150080)
0 引言
特快速暂态过电压(very fast transient overvoltages,VFTO)是由几纳秒至几十纳秒上升沿和衰减振荡的波尾组成,能引起与气体绝缘变电站直接相连的变压器绕组内部的绝缘破坏[1]。VFTO对变压器绕组绝缘的影响已经引起了国内外学者的关注,世界上一些发达国家已经开展了这方面的研究作。国内的一些电力研究院、研究所和大学等相关单位也开展了这方面的理论研究,但由于GIS产生VFTO的多样性,此类课题的相关研究仍是目前科技工作者关注的热点问题[2-3]。
VFTO作用下变压器绕组的绝缘特性、油纸绝缘配合以及沿绕组电压波传输特性都是亟待解决的工程问题,由于受到检测技术等限制,目前仍不能在实际变压器绕组上进行VFTO的相关研究,因此,只能采用绕组模型的实验方法[4]。
本文设计制作了分段层式绕组实验模型,采用毫微秒高压脉冲源、数字存储示波器、高压探头等仪器对该层式绕组特快速暂态过电压分布特性进行了实验,分别对分段层式空心绕组和分段层式有铁心绕组模型注入特快速暂态过电压,采集记录绕组模型各单元节点电压信息,得到绕组不同节点的电位分布。同时根据入波电压和绕组模型各个单元的响应电压信息求出分段层式绕组传输函数的幅频特性,并分析了谐振频率。为此类变压器绕组的绝缘设计提供理论依据。
1 实验模型
实验模型分为4段每段5层,其基本参数:总匝数为604匝;平均匝长为0.745 m;总长为480 m;绝缘相对介电常数为4.5;绕组高度为800 mm;绕组电抗高度为765 mm;绕组内半径为226 mm;绕组外半径为248 mm;铁心直径为215 mm;绝缘纸厚度为0.17 mm的青壳纸加聚酯薄膜;导线净尺寸厚度为1.12 mm,高度为1.45 mm;含绝缘漆的导线尺寸厚度为4.75 mm,高度为5.02 mm。
绕组模型如图1所示,该分段层式绕组模型是在某变压器厂设计制作的,专门用于层式变压器绕组绝缘特性的基础研究。绕组的每层有1根引出线作为测量线。分段层式绕组模型分为4段,每段5层,根据其结构特点,以绕组的每层为1个单元,故模型共分为20个单元。
绕组模型等值电路如图2所示,由上至下每单元节点的引线序号依次记作 1,2,3,4,…,20,21。该分段层式绕组模型的等值电路中相关参数计算见文献[5],在此不再赘述。

图1 分段层式绕组模型Fig.1 The winding model with subsection and layer structure
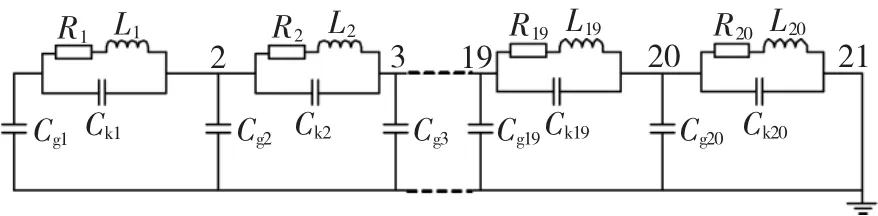
图2 分段层式绕组模型等值电路Fig.2 The winding equivalent circuit with subsection and layer structure
2 实验过程
实验工作是在室温20℃、相对湿度40%的环境下进行的。为防止高频电磁信号的干扰,确保采集记录的信号准确可靠,实验仪器之间的连接采用屏蔽线。
2.1 实验仪器与实验系统
实验测量装置由脉冲电压发生器、示波器、高压探头、分段层式绕组模型及测量屏蔽线组成。具体实验仪器如下:
1)脉冲电压发生器选用的是GMY-1型毫微秒高压脉冲源。
2)示波器选用的是Tektronix TPS2014数字存储示波器。
3)高压探头选用的是Tektronix P5210高压有源差分探头。
实验过程,VFTO脉冲电压由GMY-1型毫微秒高压脉冲源提供,应用Tektronix TPS2014示波器实时采集存储各单元节点的响应信号,并应用现代信号处理技术,由PC计算机对所采集得到的实验数据进行分析处理。该分段层式绕组模型的实验系统如图3所示。

图3 分段层式绕组模型实验系统Fig.3 Experimental setup of winding model
2.2 实验结果与分析
为探索分段层式绕组VFTO脉冲下暂态过程的电磁关系,实验分两种情况进行,即分段层式绕组中有铁心和无铁心。通过实验比较此绕组电位分布的异同,分析铁心对绕组暂态过程的影响。由GMY-1型毫微秒高压脉冲源提供的VFTO脉冲电压波形如图4所示。

图4 VFTO波形Fig.4 The VFTO waveform
实验过程将此视在波前时间为10 ns、幅值为450 V的VFTO脉冲电压分别施加在绕组模型的首端、中部和末端,实测各个单元的电压波形,根据各单元的电压波形拟合沿绕组的电位分布,研究分析VFTO作用下层式绕组电位分布规律。
2.2.1 有铁心绕组
在铁心存在的分段层式绕组模型首端注入视在波前时间为10 ns、幅值为450 V的VFTO脉冲电压,绕组末端经一导线接地。用示波器测量各个单元的电压波形。由于单元数目较多,本文中只列出了第1、5、10、15、20单元电压波形,如图5所示。
有铁心首端入波试验结果可以看出,首端注入该VFTO脉冲电压,电位分布如图6所示,从图中可以看出,绕组段间的电压梯度分布极不均匀,最大梯度电压变化出现在首段结尾处,其最大击穿电压也就出现在靠近绕组首端的很小区域。因此,该区域绕组绝缘所受冲击是最为严重的。
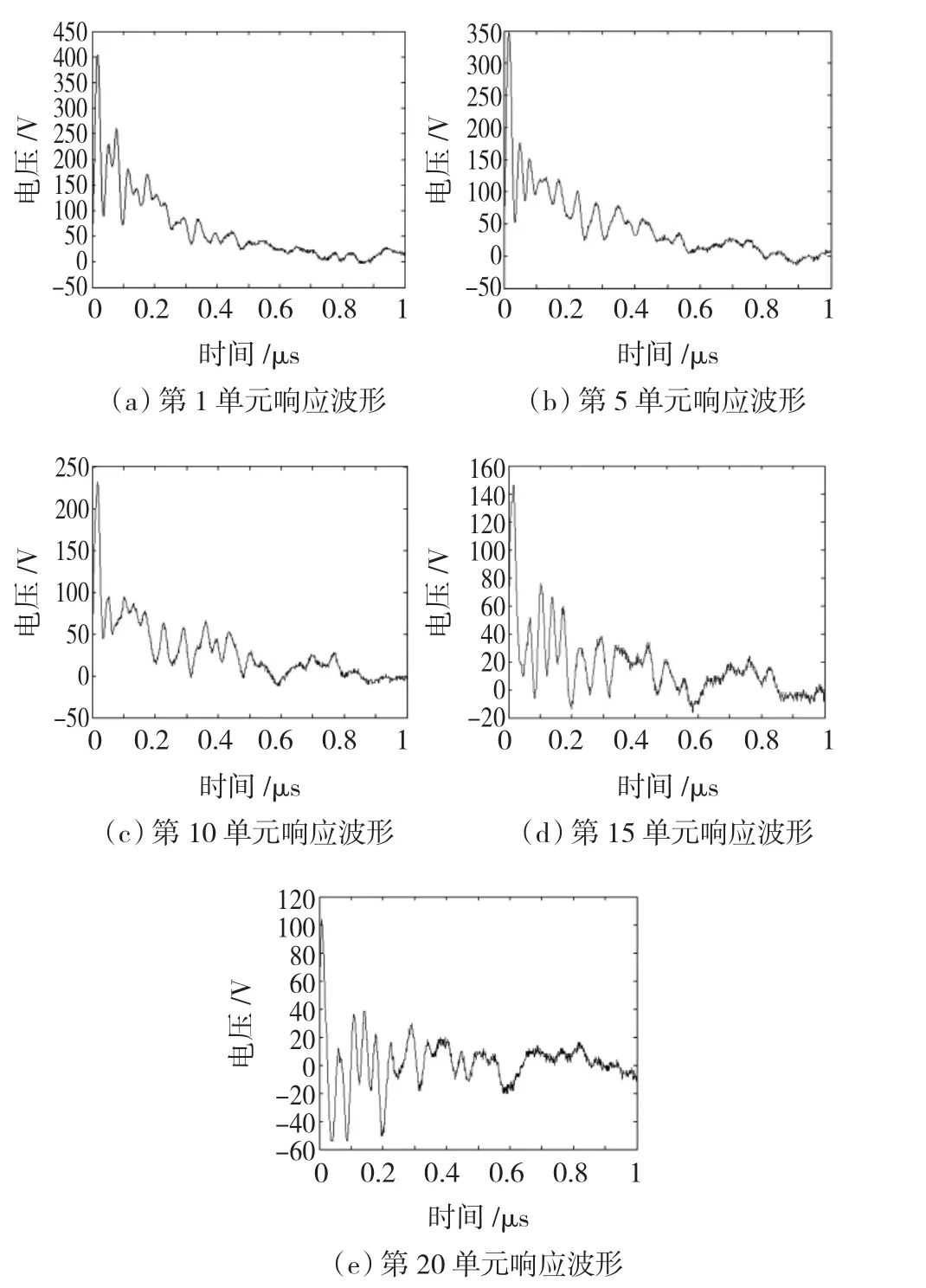
图5 第1、5、10、15、20单元电压测试波形Fig.5 Voltage waveforms at the 1st,5th,10th,15th and 20th unit

图6 首端入波电位分布Fig.6 Potential distribution of input wave at the winding head-end
在铁心存在的分段层式绕组模型中部注入视在波前时间为10 ns、幅值为450 V的VFTO脉冲电压,绕组末端经一导线接地。用示波器测量第1、5、10、15、20单元电压波形,如图7所示。

图7 第1、5、10、15、20单元电压测试波形Fig.7 Voltage waveforms at the 1st,5th,10th,15th and 20th unit
由铁心中部入波的电位分布曲线图8可以看出,最大电位梯度变化出现在靠近入波节点的前几个单元,说明在这个区域的绕组绝缘所受的冲击最为严重,此处绝缘易被击穿。
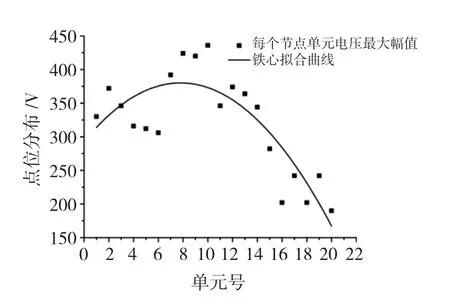
图8 中部入波电位分布Fig.8 The potential distribution of input wave at the winding middle
铁心存在的分段层式绕组模型末端注入视在波前时间为10 ns、幅值为450 V的VFTO脉冲电压。用示波器测量第1、5、10、15、20单元电压波形如图9所示。

图9 第1、5、10、15、20单元电压测试波形Fig.9 Voltage waveforms at the 1st,5th,10th,15th and 20th unit
铁心下绕组末端入波试验结果可以看出,末端注入该VFTO脉冲电压,电位分布如图10所示,从图中可以看出,最大电位梯度变化出现在第4段,说明该区域绕组绝缘所受的电压冲击最为严重。所以,末端入波时该区域绕组的绝缘欲度要特别考虑。

图10 末端入波电位分布Fig.10 Potential distribution of input wave at the winding tail-end
2.2.2 无铁心绕组
在空心分段层式绕组模型首端注入视在波前时间为10ns、幅值为450V的VFTO电压信号,绕组末端经一导线接地。用示波器测量第1、5、10、15、20单元节点的电压波形,如图11所示。

图11 第1、5、10、15、20单元电压测试波形Fig.11 Voltage waveforms at the 1st,5th,10th,15th and 20th unit
空心首端入波试验结果可以看出,该VFTO脉冲电压,电位分布如图12所示,从图中可以看出。最大电位梯度变化出现在第5单元与第6单元之间,说明该区域的绕组绝缘所受冲击最为严重。
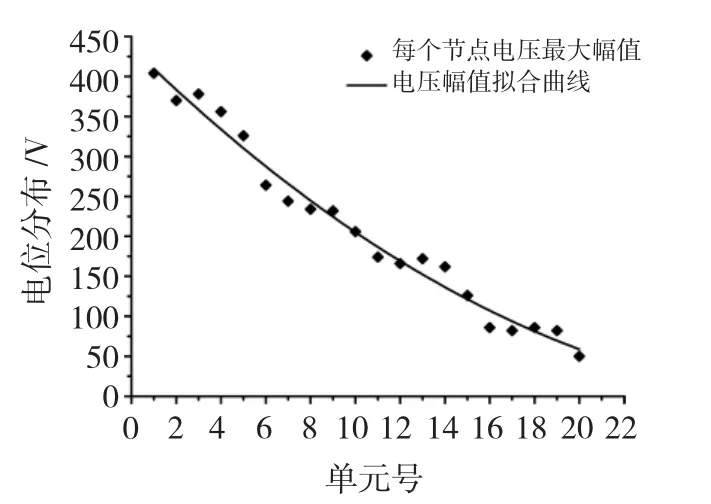
图12 首端入波电位分布Fig.12 Potential distribution of input wave at the winding head-end
在空心分段层式绕组模型中部注入视在波前时间为10 ns、幅值为450 V的VFTO电压信号,绕组末端经一导线接地。用示波器测量第1、5、10、15、20单元的电压波形,如图13所示。

图13 第1、5、10、15、20单元电压测试波形Fig.13 Voltage waveforms at the 1st,5th,10th,15th and 20th unit
空心中部试验结果可以看出,中部注入该VFTO脉冲电压,电位分布如图14所示,从图中可以看出,最大电位梯度变化出现在第15单元与第16单元之间,说明该区域的绕组绝缘所受冲击最为严重。
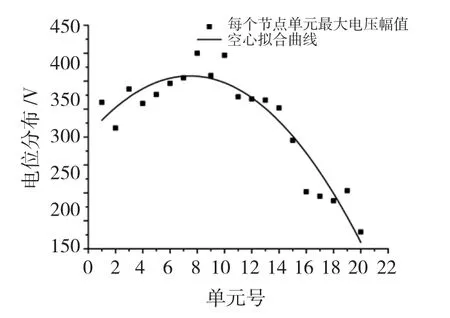
图14 中部入波电位分布Fig.14 The potential distribution of input wave at the winding middle
在空心分段层式绕组模型末端注入视在波前时间为10 ns、幅值为450 V的VFTO电压信号。用示波器测量第 1、5、10、15、20单元的电压波形,如图15所示。
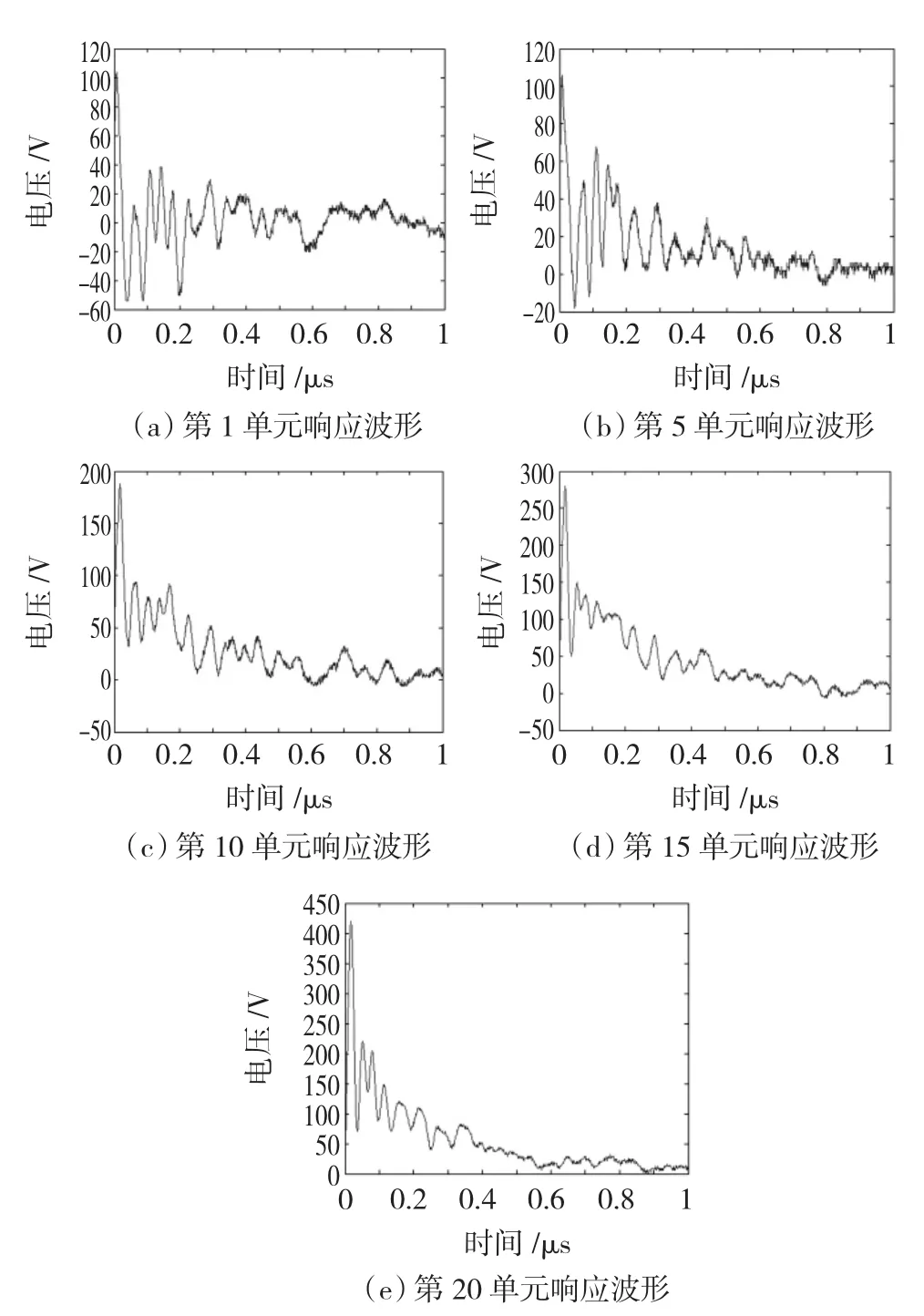
图15 第1、5、10、15、20单元电压测试波形Fig.15 Voltage waveforms at the 1st,5th,10th,15th and 20th unit
空心末端入波试验结果可以看出,末端注入VFTO脉冲电压,电位分布如图16所示,从图中可以看出,最大电位梯度变化出现在末端的最小区域内,说明该区域的绕组绝缘所受冲击最为严重。

图16 末端入波电位分布Fig.16 Potential distribution of input wave at the winding tail-end
2.2.3 结果分析
由图5~图16中的每个单元电压波形可以看出,同一端点入波时,对应测试的铁心和空心各单元电压波形明显不同。有铁心时,测试的每个单元波形随时间在绕组传播过程中,振荡的幅度比空心时大,并且离入波端点越远的单元波形振荡越明显,但波形第一个峰值变化较小。图17是首端和中部入波,在视在波前时间为10 ns、幅值为450 V的VFTO脉冲电压作用下,分段层式绕组模型有铁心和无铁心时的电位分布。发现绕组中有铁心时,同一单元的电压幅值相比于空心时的电压幅值较大,尤其是波形的第一个峰值最为明显。而空心时,绕组每经过一段,测试的波形最大幅值都有一个明显降低。主要原因:(1)电压在传播过程中出现了复杂的折反射,电磁波在物体表面绕射,随测试点远离入波信号源,使脉冲电压信号的幅值逐渐减小。另外,铁心存在时每个单元测试信号波形随时间的推移发生较大振荡,这是由于远离入波信号源的各个测试点信号在铁心表面折反射不同所引起的;(2)铁心存在时,绕组中注入脉冲电压后,它瞬间产生一个外磁场B0,在外磁场B0的力矩作用下,铁心中各磁分子环流的磁矩在一定程度上沿着场的方向排列起来。这时铁心磁棒被磁化了。磁化了的铁心就像一个由磁化电流组成的“螺线管”。这个螺线管产生的磁感应强度为B1,B1与B0在铁心内部的方向一致,因而铁心内总的磁通量增加了。磁通量增加磁场强度也随之增加。所以,同一测量点上铁心时的磁场强度都比空心时的磁场强度大。磁场强度的表达式为H=Iω/L,I、ω、L 分别为电流强度、绕组匝数、磁路长度,后两个变量相同的情况下,磁场强度越大则电流强度越大,单位绕组长度上的电压也越大[6]。所以,该层式绕组同一节点时有铁心电压幅值要比空心时电压幅值大。
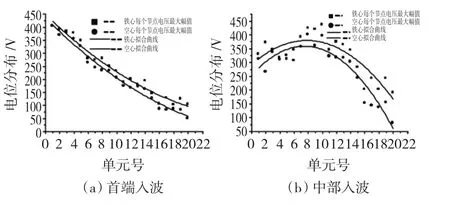
图17 有铁心和无铁心下绕组的电位分布Fig.17 The winding potential distributions with and without core,respectively
3 幅频特性分析
变压器绕组中的幅频特性分析主要是通过建立变压器绕组的单输入多输出的多端口模型进行分析。VFTO中含有的震荡谐振频率与变压器绕组中的若干固有频率匹配,可能引起谐振过电压,从而破坏绕组的层间匝间绝缘。所以,根据得到的多端口模型求出传输函数,通过对传输函数进行分析获得变压器绕组中的谐振相关信息,从而确定谐振频率宽度,对谐振可能发生的位置进行定位[7-8]。
VFTO脉冲电压信号在该绕组模型传播过程中,可以认为整个传输系统是由多个单元多个子传输系统构成的一个复杂的传输函数系统,如图18给予了描述。由传输函数理论可知,一般用h(n)表示传输函数,即

式中:h(n)为传输函数;Y(n)为系统输出响应;X(n)为系统输入信号。通过傅里叶变换,可以把式(1)转变到频率域,即

式中:h(ejω)为频率域下传输函数;Y(ejω)为频率域下系统输出响应;X(ejω)为频率域下系统输入信号[9]。

图18 复杂传输系统Fig.18 Transmission system of transformer winding
整个系统的传输函数为

式中:H(ejω)为整个系统频率域下的传输函数;hi(ejω)为第i个单元测试的VFTO脉冲响应与注入VFTO脉冲信号相比所求出的频率域下子传输函数。
本文采用矢量匹配法对所得的传输函数进行了拟合,得到了绕组各个单元的电压传输函数的幅频特性曲线。并对幅频特性曲线进行分析,即可确定该层式绕组试验模型的谐振频率。
在分段层式绕组模型首端施加VFTO脉冲电压,实测绕组各单元的响应电压,根据入波电压和响应电压求出分段层式绕组电压传输函数的幅频特性。为了更加清楚地描述铁心对幅频特性曲线的影响,实验分两种情况进行,即绕组中有铁心和无铁心,比较谐振频率范围的异同。
3.1 有铁心
在有铁心的分段层式绕组模型首端施加VFTO脉冲电压信号,测得绕组各端响应电压,根据实测数据由式(3)求得绕组各单元的传输函数。图19给出了绕组第3、4、5、8单元末端电压传输函数幅频特性。

图19 第3、4、5、8单元幅频特性Fig.19 The amplitude and frequency characteristics of the 3th,4th,5th,8th unit
从图19中可以看出,绕组的主要谐振频率集中在0.5~3 MHz之间,说明此频段的信号最易引起绕组的电磁谐振。当频率小于0.5 MHz或者大于3 MHz时,幅值迅速降低,此频段的信号对该绕组的绝缘危害性不大。
3.2 无铁心
在无铁心的分段层式绕组模型首端施加VFTO脉冲电压信号,测得绕组各端响应电压,根据实测数据由式(3)求得绕组各单元的传输函数。图20给出了绕组第3、4、5、8单元末端电压传输函数幅频特性。

图20 第3、4、5、8单元幅频特性Fig.20 The amplitude and frequency characteristics of the 3th,4th,5th,8th unit
从图20中可以看出:1)绕组的主要谐振频率集中在1.5~3 MHz之间,说明此频段的信号最易引起绕组的电磁谐振,当频率小于1.5 MHz或者大于3 MHz时,幅值迅速降低,此频段的信号对该绕组的绝缘危害性不大;2)空心绕组与有铁心绕组谐振频率范围有较大差别,主要原因是空心绕组电感、电容等参数比有铁心电感、电容等参数小的多,所以入波电压相同的情况下响应电压、传输函数幅频特性都会发生变化。这造成空心绕组谐振频率宽度小于有铁心绕组时的谐振频率宽度。
4 结语
根据以往VFTO对变压器饼式绕组绝缘性能影响的研究,本文针对VFTO作用于分段层式绕组绝缘特性进行分析。通过实验对分段层式绕组模型注入VFTO信号,并测试了各单元节点电压波形。分析了VFTO信号作用于有铁心和空心绕组模型时各单元的电位分布规律和谐振频率响应特性。实验结果表明,最大梯度电压出现在入波端点相邻的单元附近。有铁心时,单元的电压幅值相比于空心时的单元电压幅值较大,说明铁心存在时的层间梯度电压较空心时小,这为分段层式绕组绝缘结构的合理设计提供了依据。铁心存在时的谐振频率宽度要比空心时宽,说明空心时VFTO的谐振频率与分段层式变压器绕组的固有频率相匹配概率较小,不容易造成绝缘击穿。目前,世界上还没有VFTO脉冲电压作用于分段层式绕组模型的实验研究。本文可为VFTO作用于分段层式绕组的绝缘性能的研究提供实验依据。
[1]孙海峰,梁贵书.VFTO作用下变压器绕组的谐振分析[J].高电压技术,2006,32(6):1-4.
SUN Haifeng,LIANG Guishu.Analysis of resonance in transformer windings under very fast transient overvoltages[J].High Voltage Engineering,2006,32(6):1-4.
[2]张喜乐.VFTO对电力变压器影响的时域仿真计算及实验研究[D].保定:华北电力大学,2008.
[3]胡文堂,李思南,万启发.变压器绕组的陡波电压分布特性[J].高电压技术,2006,32(11):57-60.
HU Wentang,LI Sinan,WAN Qifa.Steep front Impulse voltage distribution characteristics of transformer windings[J].High Voltage Engineering,2006,32(11):57-60.
[4]赵凯华,陈熙谋.电磁学[M].北京:高等教育出版社,1985:549-552.
[5]胡金星.特快速暂态过电压下变压器绕组的建模与仿真的研究[D].重庆:重庆大学,2005.
[6]桂峻峰,高文胜,谈克雄.变压器绕组局部放电脉冲响应的相关分析及电气定位[J].清华大学学报,2003,43(3):304-306.
GUI Junfeng,GAO Wensheng,TAN Kexiong.Correlation of partial discharge pulse signals in transformer windings to locate discharge locations[J].Journal of Tsinghua University,2003,43(3):304-306.
[7]何青,王赞基.变压器线圈暂态的频域分析[J].清华大学学报,1995,1(35):39-45.
HE Qing,WANG Zanji.Frequency domain analysis of the transient in the transformer winding[J].Journal of Tsinghua University,1995,1(35):39-45.
[8]白少佐.局部放电信号在干式变压器绕组中的传播特性研究[D].哈尔滨:哈尔滨理工大学,2008.
[9]郑殿春,窦玉雷,王新月.暂态电压下变压器线圈电感参数的计算[J].哈尔滨理工大学学报,2010,15(5):31-34.
ZHENG Dianchun,DOU Yulei,WANG Xinyue.Calculation on inductance parameters of transformer winding applied transient voltage[J].Journal of Harbin University of Science and Technology,2010,15(5):31-34.

