双初级耦合直线感应电动机集总参数模型

马名中， 马伟明， 张育兴， 王公宝， 李卫超

(1．海军工程大学舰船综合电力技术国防科技重点实验室，湖北武汉 430033;2．西安交通大学电气工程学院，陕西西安 710049)

0 引言

直线感应电动机(linear induction motor，LIM)可以提供直线驱动力，无需其他中间转换机构作为传动装置即可将电能转换为直线运动的机械能，因此在轨道交通、矿井提升等场合有着越来越广泛的应用［1－3］。依据不同的应用场合，直线电机外形可以设计为扁平形、圆筒形、盘形以及无槽环形等结构。针对上述直线感应电动机，文献［4－9］对其工作原理、数学模型、参数计算以及边端效应等性能进行了非常详尽的研究。但对于两台电机初级绕组上下并联布置共用一个次级结构的双初级耦合直线感应电动机，很少有文献报导。这种结构中初级绕组可以串联运行、并联运行或者采用独立电源供电，在相同电压电流约束条件下能使两台电机产生的电磁推力共同作用于同一个次级，甚至可以采用“堆积木”的方式推广应用于多定子结构(N≥2)来进一步提高电磁推力，因此在动子进行高速大推力运动的场合有着明显优势，特别是在汽车碰撞试验或电磁发射领域有着广阔的应用前景［10－12］。

双初级耦合直线感应电动机由于上下两台电机初级绕组层叠布置，当初级绕组同时通入电流时，导致定子铁心边缘气隙磁场间存在着磁路耦合;同时，由于次级共用一块铝板，次级动子板上的感应涡流也必然存在着路径耦合。因而深入研究这种多定子结构的耦合关系对电机动态性能的影响，对于提高电机的运行性能具有重要意义。

本文从常规单定子直线感应电动机气隙磁场和感应流场出发，详尽分析了双初级耦合直线感应电动机初级绕组边缘气隙磁场及次级动子板上电涡流耦合关系。针对电机单定子工作、上下定子通入同向电流或反向电流等不同工况，统一了电流闭环工作模式下的集总参数控制模型，并利用电机堵转时的电磁推力对电机参数进行了辨识。理论分析和实验结果吻合较好，为今后该类型电机的应用和控制策略的实现奠定了理论基础。

1 双初级直线电机耦合关系

直线感应电机气隙磁场H，由初级绕组通电电流产生的磁场Hs和次级感应涡流产生的磁场Hr叠加而成［12］，为

在空载情况下，单定子直线感应电机气隙中磁场强度Hs可以表述为［13］

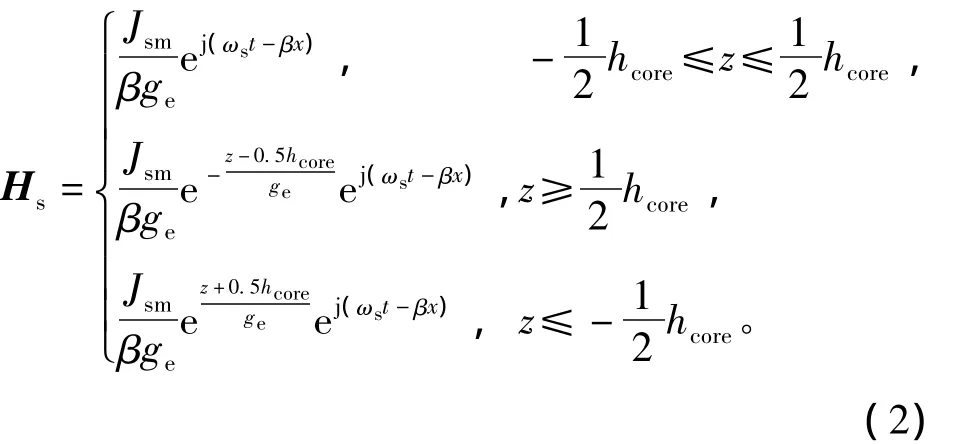
式中Jsm为初级绕组等效面电流峰值;ωs为滑差角频率;β=π/τ为直线电机线速度/角速度转换系数，τ为电机极距;hcore为定子铁心高度;ge为等效空气间隙，其值为［13－14］

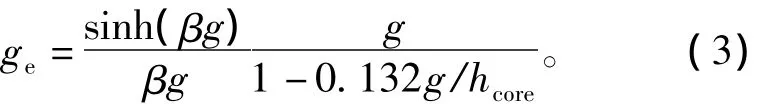
与单定子直线感应电动机不同，双初级耦合直线感应电动机由于初级层叠布置，导致初级绕组间存在边缘气隙磁场之间的耦合。由式(2)可知，Hs与Jsm方向定义有关，当上下初级绕组同时通入同向电流时，定子铁心中部边缘气隙磁场相互耦合导致场强增强，如图1(a)所示;当上下初级同时通入反向电流时，定子铁心中部边缘气隙磁场相互抵消导致场强减弱，如图1(b)所示。

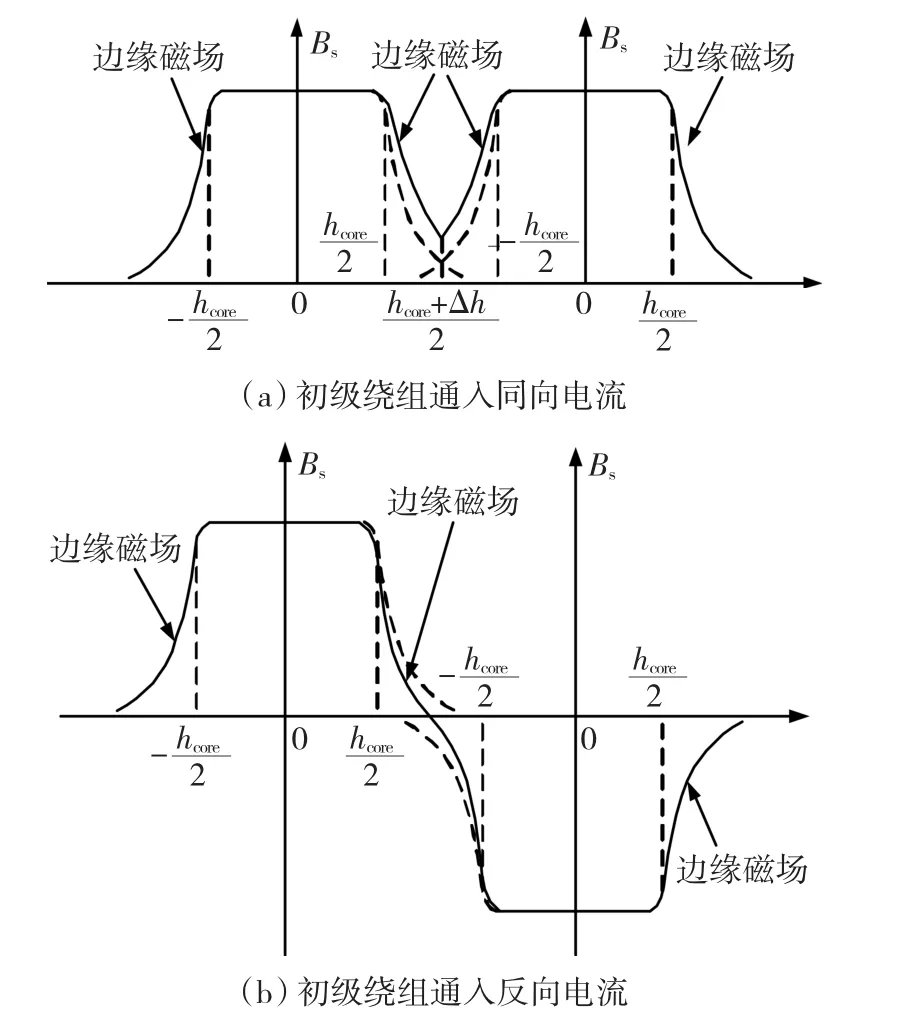
图1 双初级直线感应电机边缘气隙磁场耦合关系Fig．1 Magnetic coupling sketch of double-primary LIM

另一方面，利用电磁方程

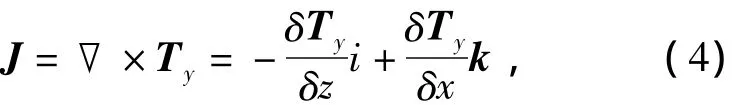
可以得到单定子直线感应电动机次级动子板上的感应涡流如图2(a)所示。然而，双初级直线感应电动机由于次级共用一块铝板，次级感应涡流存在着路径耦合。当初级绕组同时通入同向电流时，次级动子板中部的横向涡流相互抵消，即在满足式(4)的同时，增加了边界条件

式中h为上下定子铁心间距。上述边界条件将使得动子板上的涡流形成一个大循环路径，如图2(b)所示;当初级绕组同时通入反向电流时，次级动子板中部的横向涡流则由于相互叠加而增大，如图2(c)所示。

图2 双初级直线感应电机次级涡流场耦合关系Fig．2 Faradic coupling sketch of double-primary LIM

双初级耦合直线感应电动机由于上述耦合关系的存在，导致其在模型建立、参数提取等方面与传统单定子直线感应电动机的分析方法完全不同。

2 双初级直线电机集总参数模型

2.1 边端效应对电机参数测量的影响

传统旋转电机参数测量，均是针对如图3所示的稳态T型等效电路，利用电机的空载及堵转试验的端口电压/电流计算求取。公开发表的文献资料对直线感应电机参数的提取，依然沿袭了旋转电机参数测量的方法［15］。

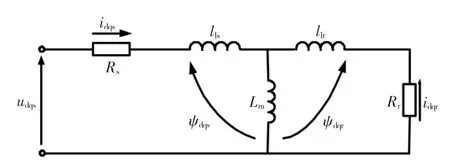
图3 传统感应电机稳态T型等效电路Fig．3 Static T type equivalent circuit of traditional LIM

然而，直线感应电机与传统旋转电机相比，由于端部开裂存在着纵向边端效应，致使其等效电路的参数分析较旋转电机复杂。文献［16－17］对单初级双边直线感应电动机研究表明，由于静态纵向边端效应影响，初级三相绕组互感严重不平衡，当三相不对称绕组通入三相对称电压时，三相电流幅值及相角不对称，即三相电流中不仅包含正序分量，而且包含零序分量和负序分量。直线感应电动机的工作原理是利用电流的行波磁场来产生电磁推力，负序电流的存在导致电机运行过程中包含反向的电磁推力，对电机动态性能造成不利影响。因此利用常规旋转电机的稳态T型等效电路、以及电机的空载及堵转试验来求取本文研究的双初级耦合直线感应电机模型和参数存在一定的不足之处。

2.2 集总参数模型

直线感应电动机控制系统的设计，通常是采用对定子电流的闭环控制，来实现对电磁推力的精确调节，因此所有定子电流是可控的［18］。双初级耦合直线感应电动机在运行过程中，可以通过控制系统对两台电机定子三相绕组施加三相不对称电压，使得上下定子电流幅值相等，空间相位一致或者相差180°，此时双初级耦合直线感应电机存在如下3种不同工况:

(1)单定子工作

假设Rsk、Llsk、Lmk(k=1，2)分别为上下电机的初级绕组电阻、漏电感和激磁电感，Rrk、Llrk(k=1，2)分别为上下电机的次级等效电阻和等效漏感，则上定子或下定子单独工作时与常规直线感应电机完全相同。

(2)上下定子电流幅值相等，空间相位一致

假设Lm12、Lm21为上下定子间的耦合互感，则当上下定子电流幅值相等，空间相位一致时

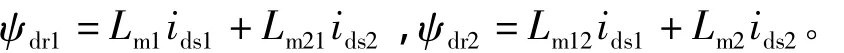
另一方面，将Rrk、Llrk(k=1，2)进行分解，假设Rrx为次级中部横向电阻，Rrp1、Rrp2分别为上下电机次级除中部横向电阻以外的其它等效电阻;Llrx为次级中部横向漏感，Llrp1、Llrp2分别为上下电机次级除中部横向漏感以外的其它等效漏感。即

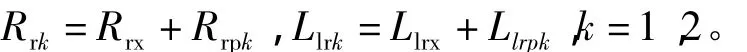
当双定子耦合直线感应电动机工作在这种工况时，上下电机次级的实际等效电阻及漏感分别为:

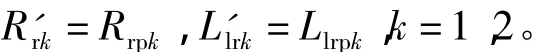
(3)上下定子电流幅值相等，空间相位差180°

当双定子耦合直线感应电动机上下定子电流幅值相等，空间相位相差180°时，有

综合上述3种工况，可以得到该电机恒流工作模式下的稳态等效电路如图4所示。

为了方便表述，令

由于初级绕组边缘气隙磁场及次级涡流耦合关系的存在，将导致L'm、R'r及L'lr均为非对角阵，初/次级之间的耦合关系强弱由L'm、R'r及L'lr中非对角位置的非零元素体现。

图4 双初级耦合直线感应电机稳态等效电路Fig．4 Static equivalent circuit of double-primary LIM

2.3 集总参数辨识

当双初级耦合直线感应电动机采用间接矢量控制，并且控制上下两台电机定子磁链在空间上同相位，则可以建立其电流可控T型集总参数稳态等效电路如图5(a)所示。此时选择同步dq轴坐标系统，使d轴与励磁电流im同相位，并通过将次级侧漏感折算到电机定子侧，电机模型可以简化为同步dq轴坐标系下电流可控L型集总参数稳态等效电路，如图5(b)所示。

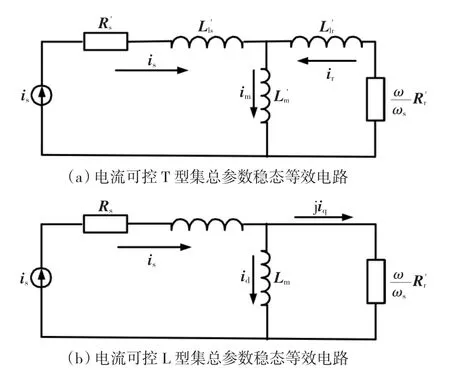
图5 双定子耦合直线感应电机集总参数等效电路Fig．5 Lumped-parameter equivalent circuit of double-primary LIM

依据变换前后端口电压及功率不变原则，可以得到图5(b)所示L型等效电路中参数满足如下关系

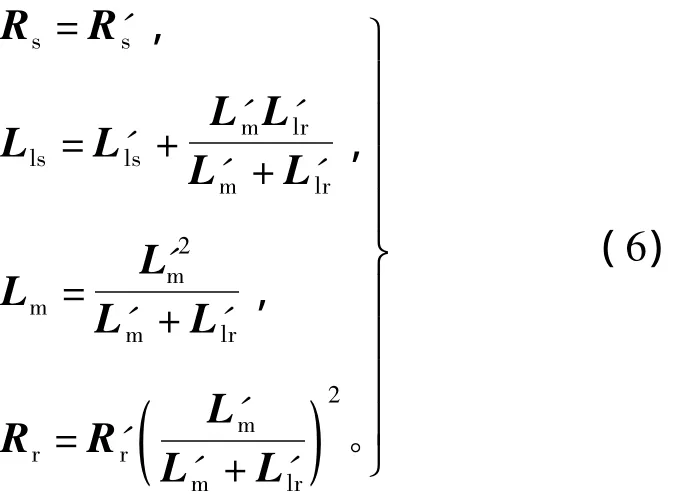
同时由基尔霍夫电压回路方程及电流定律可得

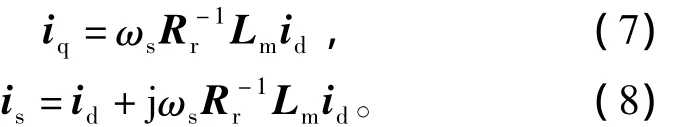
等式(8)表明，对于任意给定的励磁电流id及转差频率ωs，可以得到相应定子电流来维持与动子交链的磁链不变。利用动子上消耗的总功率，减去动子电阻损耗功率，可以得到多定子直线感应电动机跨过电磁气隙传输到动子上的机械功率为

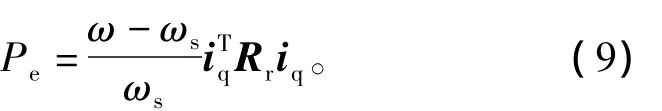
则直线电机的输出电磁推力为

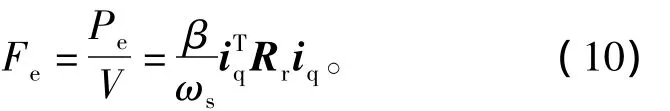
将等式(7)代入等式(10)得

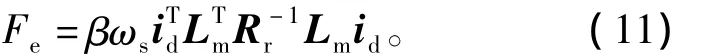
利用等式(7)、等式(8)及等式(11)即可对电机集总参数Lm及Rr进行辨识。

3 实验验证

为了验证本文集总参数模型分析及参数辨识方法的正确性，利用双初级耦合直线感应电动机工程样机进行实验，该样机的基本参数:初级铁心高度hcore=52 mm;上下初级铁心间距h=15 mm;单边机械气隙g=5 mm;次级动子板材料为铝板，厚度d=4.5 mm。

实验过程中，逆变器将1 000 V蓄电池组直流源转换成三相电压给直线感应电动机供电，通过电流闭环调节维持电流35 A恒定，电磁推力采用拉力计进行测量。测试内容包括双初级上下定子单独通电、双初级同时通入同向电流、双初级同时通入反向电流三种工况下频率从 5 Hz、8 Hz、10 Hz、18 Hz、19 Hz、20 Hz到60 Hz(每隔5 Hz一个测试点)时的电磁推力，测试数据和利用集总参数模型进行计算的推力－转差频率曲线如图6所示。

通过图6(b)可以看出，单台电机工作、双初级同时通入同向电流或反向电流3种工况下，整个测试频率范围内电磁推力计算值与实验测量值的峰值误差百分比分别为14.52%、9.29%及8.01%，因此集总参数模型针对双初级耦合直线感应电动机不同工况时的模型和参数得到了较好的统一。

通过图6(c)则可以得到如下结论:双初级耦合直线感应电动机由于耦合因素影响，上下初级同时通入同向电流时电磁推力要高于单台电机工作时电磁推力的2倍，而获得最大电磁推力对应的转差频率有所降低;当上下初级同时通入反向电流时，电磁推力比单台电机工作时电磁推力的2倍要小，而获得最大电磁推力对应的转差频率比单台电机工作时获得最大电磁推力对应的转差频率要高。

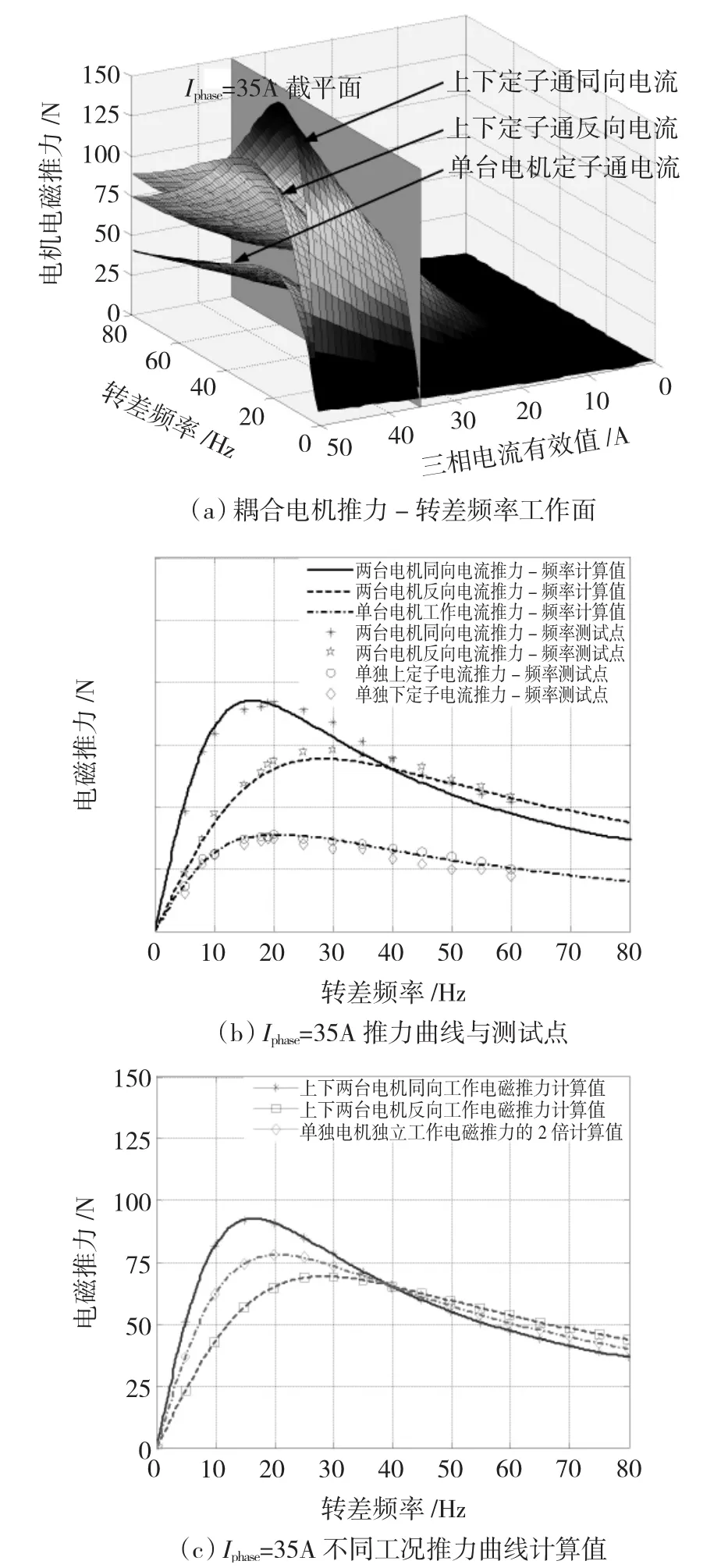
图6 不同工况下电机推力－频率曲线Fig．6 Curves of motor thrust vs slip frequency

4 结语

本文对双初级耦合直线感应电动机中初级绕组边缘气隙磁场及次级动子板上电涡流耦合关系进行了深入研究，在此基础上针对双初级耦合直线感应电动机中双初级上下定子单独通电、双初级同时通入同向电流或反向电流等不同工况，建立了统一的集总参数模型，模型计算值和实验结果吻合较好。利用该模型进行参数辨识克服了传统等效电路测量法中由于边端效应导致三相电流不对称对电机电磁推力性能的影响，而且该模型可以利用“堆积木”的方式直接推广应用于多定子结构(N≥2)直线感应电动机，为多定子直线感应电动机推的推广应用奠定了理论基础。

［1］徐伟，汪旭东，袁世鹰．交通牵引大功率单边直线感应电机性能研究［J］．电机与控制学报，2008，12(4):396－402．

XU Wei，WANG Xudong，YUAN Shiying．Performance research on high power single linear induction motor in tractive transportation［J］．Electric Machines and Control，2008，12(4):396－402．

［2］史黎明，何晋伟，王珂，等．直线感应电机间接磁场定向悬浮牵引联合控制［J］．电机与控制学报，2009，13(2):179－183．

SHI Liming，HE Jinwei，WANG Ke，et al．Combined control of levitation and propulsion for linear induction motor based on IFO method［J］．Electric Machines and Control，2009，13(2):179 －183．

［3］GUROL H．General atomics linear motor applications:moving towards deployment［J］．Proceedings of the IEEE，2009，97(11):1864－1871．

［4］KIM Daekyong，KWON Byungil．A novel equivalent circuit model of linear induction motor based on finite element analysis and its coupling with external circuits［J］．IEEE Transactions on Magnetics，2006，42(10):3407 －3409．

［5］许金，马伟明，鲁军勇．无槽双边长定子直线异步电动机二维磁场分布及电磁力计算［J］．电工技术学报，2008，23(9):38－44．

XU Jin，MA Weiming，LU Junyong．Analysis of 2-D magnetic field and calculation of electromagnetic force of slotless long stator double-sided linear induction motor［J］．Transactions of China Electrotechnical Society，2008，23(9):38－44．

［6］鲁军勇，马伟明，许金．高速长定子直线感应电动机的建模与仿真［J］．中国电机工程学报，2008，28(27):89－94．

LU Junyong，MA Weiming，XU Jin．Modeling and simulation of high speed long primary double-sided linear induction motor［J］．Proceedings of the CSEE，2008，28(27):89 －94．

［7］鲁军勇，马伟明，李朗如．高速长初级直线感应电动机纵向边端效应研究［J］．中国电机工程学报，2008，28(30):73 －78．

LU Junyong，MA Weiming，LI Langru．Research on longitudinal end effect of high speed long primary double-sided linear induction motor［J］．Proceedings of the CSEE，2008，28(30):73 －78．

［8］鲁军勇，马伟明，孙兆龙，等．多段初级直线感应电动机静态纵向边端效应研究［J］．中国电机工程学报，2009，29(33):95－101．

LU Junyong，MA Weiming，SUN Zhaolong，et al．Research on static longitudinal end effect of linear induction motor with multisegment primary［J］．Proceedings of the CSEE，2009，29(33):95－101．

［9］鲁军勇，马伟明，张育兴．次级边缘漏感对高速直线感应电机性能的影响［J］．中国电机工程学报，2010，30(15):53－57．

LU Junyong，MA Weiming，ZHANG Yuxing．Characteristic of high-speed linear induction motor considering the secondary edge leakage［J］．Proceedings of the CSEE，2010，30(15):53 －57．

［10］王福金，姚智慧．舰载机的电磁弹射器研究［J］．哈尔滨理工大学学报，2009，14(6):106－110．

WANG Fujin，YAO Zhihui．Study of electronic magnetic aircraft launch system for carrier-bome aircraft［J］．Journal of Harbin U-niversity of Science and Technology，2009，14(6):106 －110．

［11］MEEKER D C，NEWMAN M J．Indirect vector control of a redundant linear induction motor for aircraft launch［J］．Proceedings of the IEEE，2009，97(11):1768－1776．

［12］JOHNSON A P．High speed linear induction motor efficiency optimization［D］．Cambridge:Deptment of Electrical Engineering and Computer Science of Massachusetts Institute of Technology，2005:13－19．

［13］张广溢．直线电动机静态横向边端效应研究［J］．电机与控制学报，1999，3(2):126－128．

ZHANG Guangyi．Research on the static transverse end effect of the linear motor［J］．Electric Machines and Control，1999，3(2):126－128．

［14］LEE C H，CHIN C Y．A theoretical analysis of linear induction motors［J］．IEEE Transactions on Power Apparatus and Systems，1979，98(2):679－688．

［15］孙兆龙，刘德志，马伟明，等．双初级耦合直线感应电动机研究［J］．中国电机工程学报，2010，30(27):1－6．

SUN Zhaolong，LIU Dezhi，MA Weiming，et al．Double-primary coupling linear induction motors［J］．Proceedings of the CSEE，2010，30(27):1 －6．

［16］LU Junyong，MA Weiming．Research on end effect of linear induction machine for high-speed industrial transportation ［J］．IEEE Transactions on Plasma Science，2011，39(1):116－120．

［17］LU Junyong，MA Weiming．Investigation of phase unbalance characteristics in the linear induction coil launcher［J］．IEEE Transactions on Plasma Science，2011，39(1):110 －115．

［18］李卫超，胡安，马伟明，等．新型长定子直线感应电机闭环控制策略［J］．中国电机工程学报，2010，30(S):226－231．

LI Weichao，HU An，MA Weiming，et al．Control strategy of a novel double-sided long primary linear induction motor［J］．Proceedings of the CSEE，2010，30(S):226 －231．