逆变器故障诊断研究

杨巧玲，张海平

（1.兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050;2.天华化工机械及自动化研究设计院，甘肃 兰州 730060）

0 引言

电机变频调速系统中逆变器的功率半导体器件及其控制电路是最易发生故障的薄弱环节，其可靠性问题一直没有得到充分解决［1］。而最新研究也表明［2］:变频调速系统中功率变换器故障占整个驱动系统故障的82.5%。因此，有效防止逆变器故障是提高电机变频调速系统运行安全性、可靠性的根本。目前大多采取降额设计或使用并联冗余元件或电路的方法降低逆变器故障，但这两种设计方法会使电源造价过高，且仅适用于空间条件许可的场合。电力电子系统故障诊断方法有基于解析模型的方法、基于知识的方法、基于信号处理的方法等［3］。这些方法均各有优缺点，但都不能很好的解决这个问题。

本文将逆变器输出的电压信号作为特征参量，获取逆变器输出的电压频谱，利用加窗短时傅里叶变换提取逆变器输出电压的谱特征，实现逆变器的故障检测。该算法运算量较小，可以有效节约运算时间。仿真结果验证了本方法的有效性。

1 故障模式及特征分析

图1是电机逆变器驱动系统。系统运行时，工作在高频开关状态的功率管损耗较大、发热严重、发生故障的概率最大［4］，并以功率管开路和短路故障最为常见。不论发生何种故障，迅速准确的提取相应故障特征并确定故障位置对于故障后的处理至关重要。

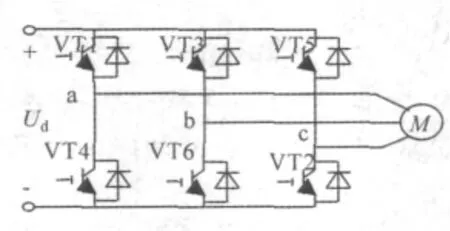
图1 无刷直流电机逆变器驱动系统

逆变器的输出电压直接反映着它的工作状态，是最为敏感的特征量。理想状态下，电机在电压对称状态下工作，各相输出电压波形一致。发生故障时，输出三相电压不对称，电机在非平衡供电状态下工作。通过对逆变器输出电压信号进行分析就能有效检测电机驱动系统的运行状态。

正常运行时，逆变器输出各相电压可表示为:

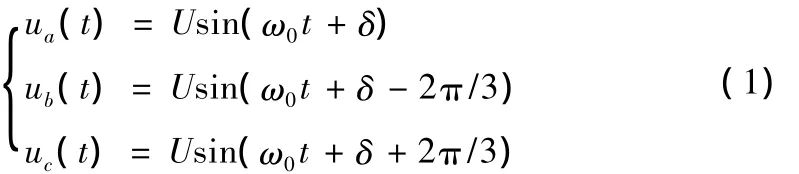
此时，若用开关函数ki等于1或0来表示功率管的闭合或断开，则逆变器输出电压满足如下关系式:

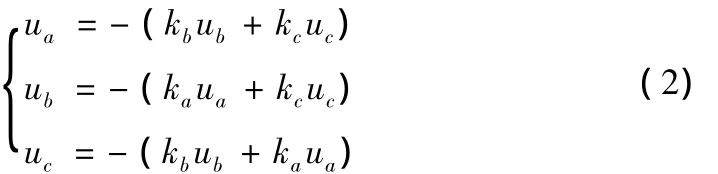
式中，ka、kb、kc为逆变器 a、b、c相开关函数。ki由调制信号与载波信号共同决定，对SPWM（Sinusoidal PWM）逆变器，将其按双傅里叶变换展开［5］，并整理得（以A相为例）:

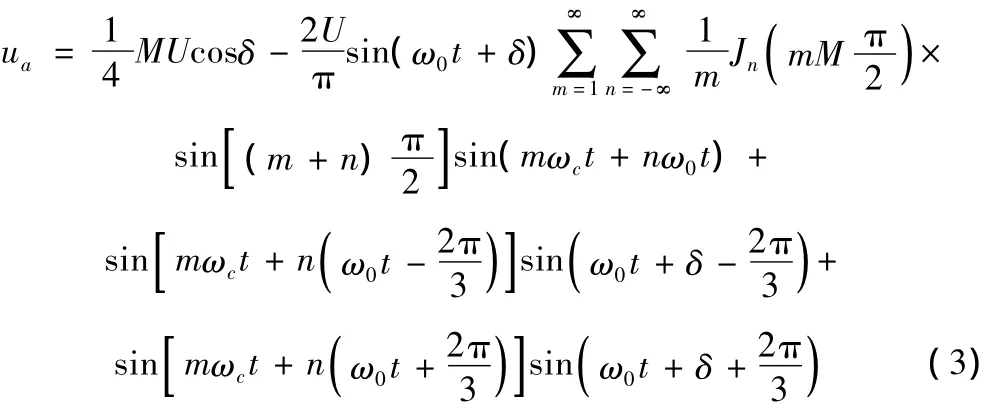
式中，第一部分为直流分量，第二部分为载波信号谐波及边频信号，在ωc远大于ω0时，对逆变器故障诊断只考虑其低频成分。正常运行时，输出相电压低频部分只包含直流成分。

当组成逆变器主电路的6个开关管中的任何一个发生了开路故障时，对应桥臂将不能正常导通。此时，输出电压的低频部分出现了其他的低频成分。以VT1管发生开路故障为例，此时A相上桥臂不再导通，逆变器的A相输出电压满足以下关系式:

输出电压不再对称，A相电压将出现负的直流分量。三相输出电流之和为零，A、C相电流出现正的直流分量［1］。分别用u'a、u'b、u'c表示故障后各相输出电压，则:

（DHT）。离散哈特莱变换定义为［8］:

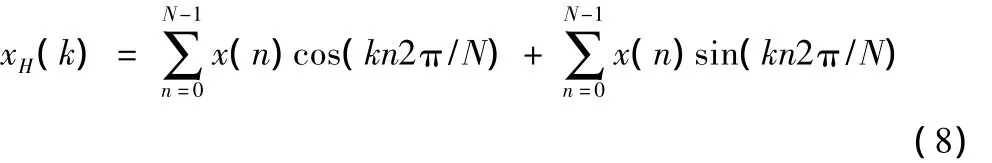
对实数x（n），xH（k）也是实数，故有:

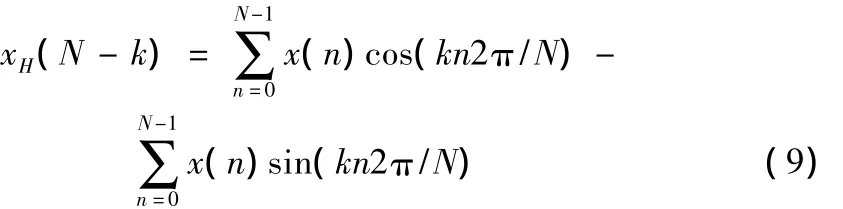
根据离散傅里叶变换与哈特莱变换的确定关系，可导出DFT和DHT 的变换关系［9］:

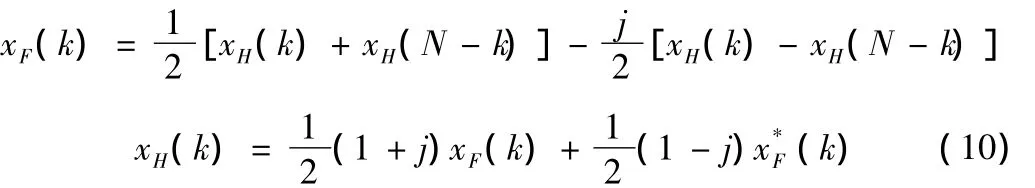
对于长度为N=2m的信号序列的DHT作时间抽取，将其分为两个长度为 N/2 的序列，即［10］:

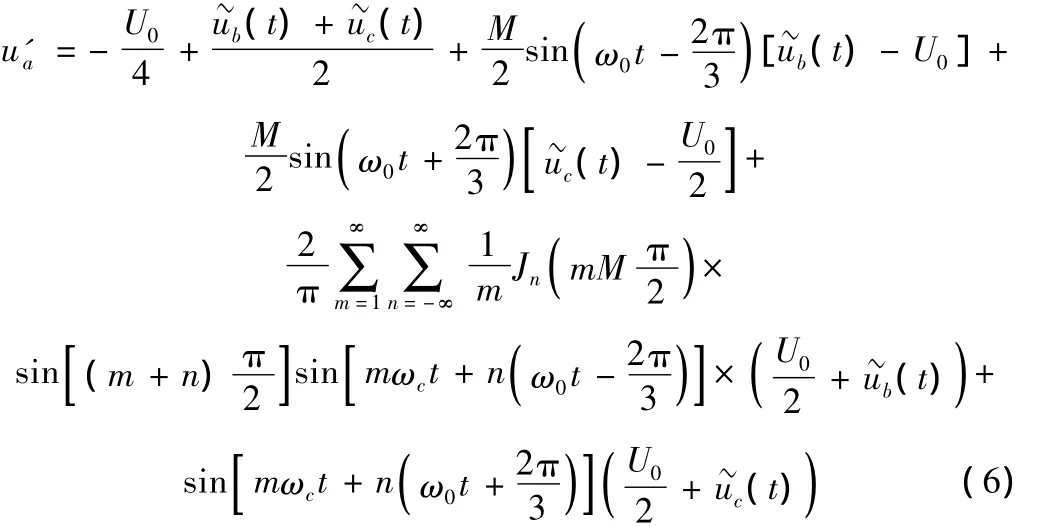
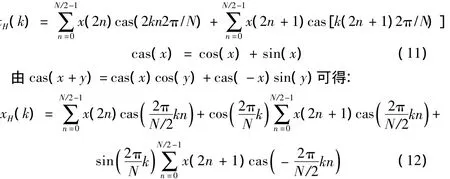
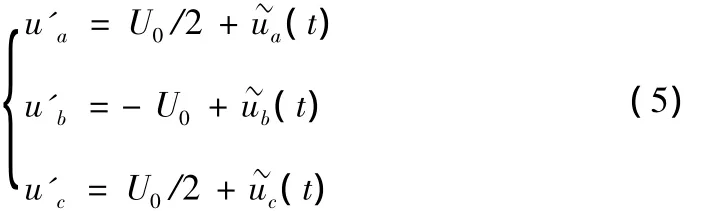
上式表明:当一个开关管发生开路故障时，逆变器的输出电压中不仅含有直流成分，还有调制信号及其谐波的频率成分，这是在逆变器正常运行时所不包含的低频成分。因此，可选逆变器输出电压频谱，作为单管开路的故障特征参量。

2 故障特征提取

故障特征提取时，若采样频率不为信号频率的整倍数则会发生谱泄漏。逆变器故障状态下的基波频率是波动的，很难保证两者的整数倍关系。严重的谱泄漏会影响信号傅里叶变换的准确性［6，7］。因此，采用加窗傅里叶变换对信号进行处理成为一种广为采用的方法。本文采用改进的加窗短时傅里叶变换算法，以得到准确的故障特征频谱。短时傅里叶变换（STFT）的基本思想是:假定非平稳信号在分析窗函数g（t）的一个短时间间隔内是平稳（近似平稳）的，并滑动分析窗函数，使f（t）g（t－τ）在不同的有限时间宽度内是平稳信号，从而计算出各个不同时刻的功率谱。信号x（t）的STFT为:

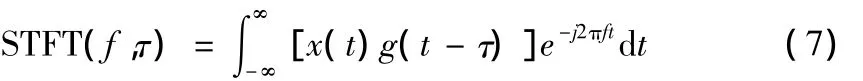
即:信号x（t）在分析时间t附近的Fourier变换（称之为“局部频谱”）。利用窗函数的滑动将信号分成一系列相互重叠的子段，并假设每个子段都是平稳的。通过对每个子段的信号加窗，减少旁瓣泄漏，然后对每一段进行离散傅立叶变换，这样得到频谱图即可表征信号的时频分布特征。离散傅里叶变换硬件实现复杂，计算时间长。R.N.Bracewell给出了快速哈特莱算法

其中0≤k≤N－1，由于cas（－x）=cos（x）－sin（x）及其周期对称性有:

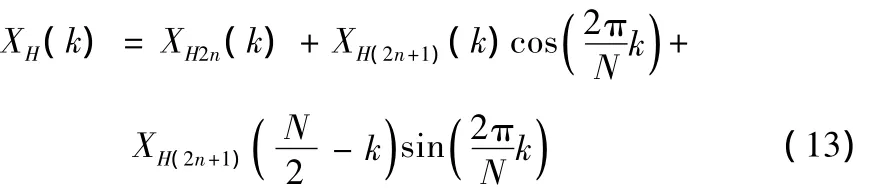
其中，X2n（k）为 X（2n）的 N/2点 DHT，X2n+1（k）为 X（2n+1）的N/2点DHT:

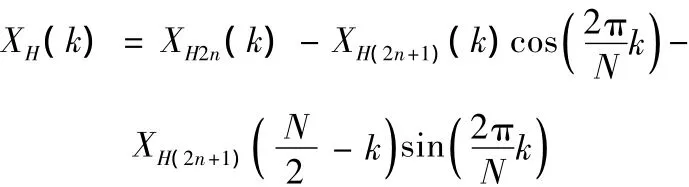
同理有:

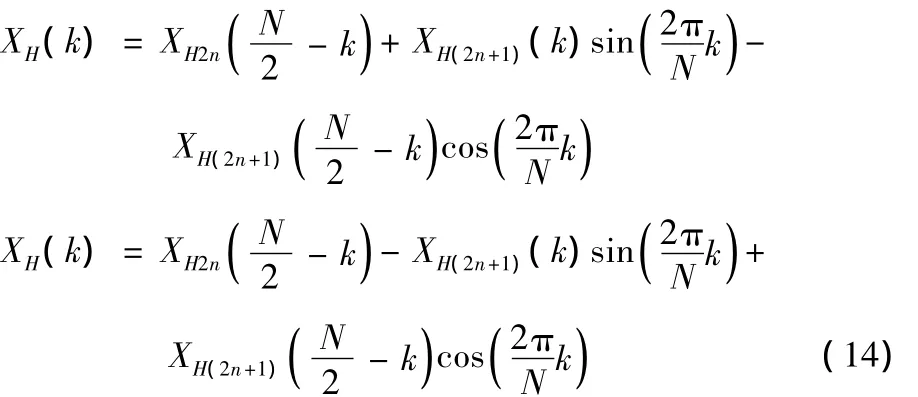
由上述四式，代入给出的XH（k）和XF（k）可求出信号序列的频谱。可以看出改进的加窗短时傅里叶变换算法运算量较小，可以有效地节约运算时间并避免谱泄露的发生。

3 仿真结果及分析

根据以上分析，对三相PWM逆变器单管开路故障进行仿真试 验，电路模型如图1所示，参数如下:直 流电压100 V，调制信号频率60 Hz。对逆变器正常运行和故障状态分别仿真，输出电压波形如图2所示:

由前面分析可知，逆 变器单管开路故障时的输出电压频谱中含有调制信号及其谐波的频率成分，对逆变器正常运行和单管开路时的输出电压进行采样，为了尽量减小谱泄漏，采用改进的加窗短时傅里叶变换算法，做快速短时傅里叶分解。得到输出电压频谱如图3、4所示。

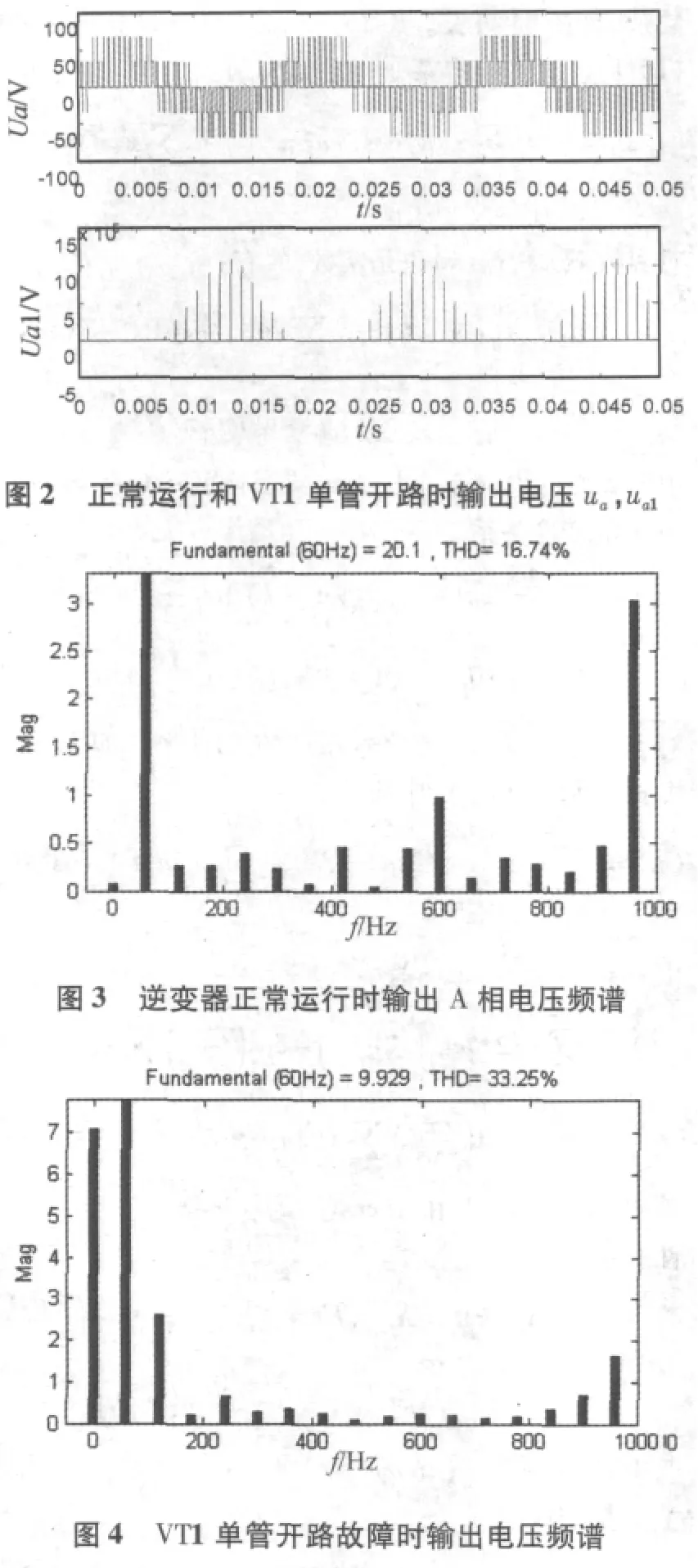
仿真试验结果表明:故障特征频率经加窗短时傅里叶变换算法分解提取后较逆变器正常运行时有明显改变，将故障时逆变器输出电压频谱与正常状态输出电压频谱作比较，可准确诊断逆变器单管开路故障。

4 结束语

对电机逆变器在正常运行及开路故障状态的输出电压特征进行了分析，并数学分析了利用加窗短时傅里叶变换对逆变器输出电压信号进行故障频谱特征提取的可行性。在此基础上，在simulink环境下搭建仿真模型进行仿真试验。试验结果表明:加窗短时傅里叶变换可有效提取逆变器故障时输出电压频谱，同时减小了谱泄漏，并可以此作为逆变器开路故障诊断的依据，实现逆变器的开路故障诊断。

［1］ Kastha D，Bose B K.Investigation of fault modes of voltage-fed inverter system for induction motor drive［J］.IEEE Transactions on Industry Application，1994，30（4）:1028 －1038.

［2］ Wikstron P W，Terens L A，Kobi H.Reliability，availability，and maintainability of high-power variable-speed drive systems［J］.IEEE Transactions on Industry Application，2000，36（1）:231 －241.

［3］蔡涛，段善旭，康勇.电力电子系统故障诊断技术研究综述［J］.电测与仪表，2008，45（509）:1 －7.

［4］汤清泉，颜世超，卢松升.三电平逆变器的功率管开路故障诊断［J］.中国电机工程学报，2008，28（21）:26－32.

［5］孟进.电力电子系统传导干扰建模和预测方法研究［D］.武汉:海军工程大学，2006.［6］ Salvatore L，Trotta A.Flap-top windows for PWM waveform processing via DFT［J］..IEE Proc.Pt.B，1988，135（6）:346－361.

［7］ Nuttal A.Some windows with very good sidelobe behavior［J］.IEEETrans.Acoustics，Speech，and Signal Processing，1981，29（1）:84－91.

［8］ Bracewell R N.Discrete Hartley transform［M］.Britain:Oxford Univ Press，1986.

［9］ HowSun Dee，Varun Jeo ti.Computing DFT using approximate fast Hartley t ransform［J］.Sixth International Symposium on Signal Processing and its Applications，2001，8（13 －16）:100 －103.

［10］ Bracewell R N.The Fast Hartley Transform［J］.Proc.IEEE，1984，（72）:1010－1018.