基于比例复数积分控制的单相逆变器并网研究

董蕾

（合肥工业大学 电气与自动化工程学院，光伏系统工程研究中心，安徽 合肥 230009）

0 引言

近年来，随着石油、煤和天然气等不可再生能源日趋紧张，节能降耗越来越被人们所重视。光伏并网发电作为太阳能利用的主要形式之一，倍受广大科研人员的关注［1］。分布式发电系统与电网接口通常采用逆变器［2，3］，并网逆变器的控制对象是网侧的电流，通过控制逆变器输出电流可以使逆变器以单位功率因数向电网供电，或对电网进行无功补偿，并网逆变器的控制性能直接影响到发电系统输出的电能质量［4］。

目前，电流控制主要可以分为线性控制和非线性控制，前者包括PI控制，重复控制等，后者包括滞环控制等。PI控制具有算法简单和可靠性高的特点，因此被广泛应用于工业过程控制，但常规的PI控制对正弦的参考电流却难以达到理想的控制效果［5］，重复控制器是基于基波周期的误差校正，其稳态性能优越，但暂态特性往往不能满足要求［6］，滞环控制具有实现简单和动态响应快的特点，但是开关频率、损耗及控制精度受滞环宽度的影响。环宽越小，控制精度越高，但开关频率和损耗将会增大［7］。

本文是根据频域分析，利用改进的PI控制器将系统的交流稳态误差控制为零，并且给出了单相系统在虚拟的伪三相静止坐标系进行坐标变换的算法，利用dq旋转坐标系中md=jmq这一关系巧妙地实现了控制器的设计.最后，仿真实验证明了此算法的有效性。

1 单相并网逆变器系统原理

1.1 系统拓扑结构

按照功率变换的级数分类，并网逆变器一般可分为单级式和多级式两种拓扑方案。图1所示为单级式逆变器的结构框图，它仅用一级能量变换就可以完成电压调整和并网逆变功能，具有电路简单元器件少可靠性高和高效低功耗等诸多优点，所以在满足系统性能要求的前提下，单级式拓扑结构将会是首选［8］。

图2为单相并网逆变器原理 图。其中直流母线由可再生能源提供，逆变桥输出经过电感 L和并网开关 S连接到电网上。电感L用于滤除开关谐波，通过适当控制使并网逆变器输出与电网电压同频同相的正弦波，实现单位功率因数并网运行［9］。

图1 单级式逆变器结构框图

1.2 线性建模及控制策略

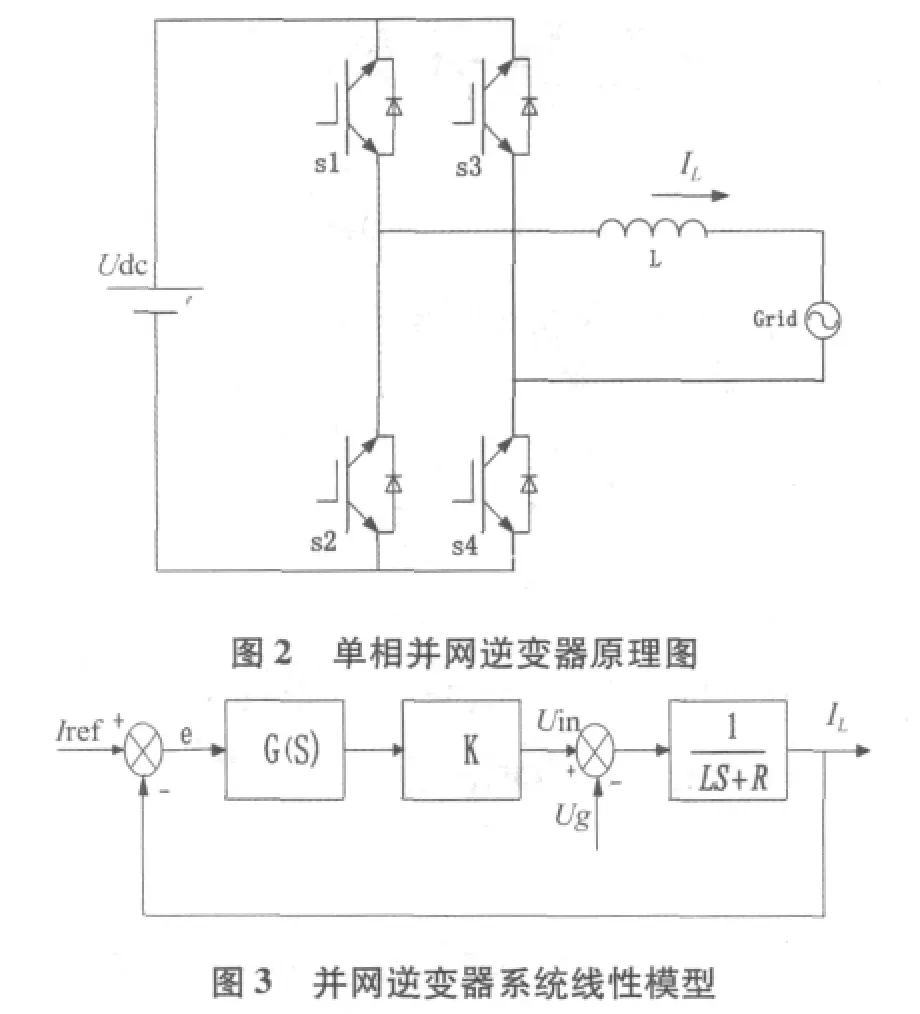
根据图2所示，建立了图3所示的控制结构图，其中，G（S）为控制器的传递函数，R为L的等效串联电阻，在忽略了小惯性时间常数下，K是PWM的等效增益。

根据图3的线性模型可得逆变器输出电流IL为:

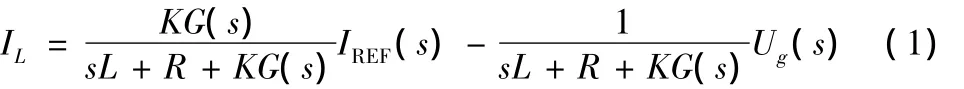
在工程中大量应用的PI控制器的传递函数为:

比例复数积分PCI控制器的传递函数为:

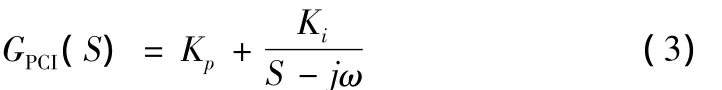
1.3 控制器在单相系统中的实现

传统PID控制器是实数域控制器，而PCI控制器中存在复数j，为复数域控制器，给控制器实现带来一定困难。复变函数理论可知，j代表幅值不变，相位正向旋转 90°。在三相系统中，利用αβ 变量mα=j mβ这一关系巧妙地实现 j［10］。然而，在单相系统中，由于只有一相电量，无法直接进行坐标变换。因此，就有必要对单相逆变系统进行旋转坐标变换的改造，从而能够在单相系统中实现复数域控制器。

在单相系统中运用旋转坐标变换的原理，设任意的单相变量（电压或者电流）的表达式为:

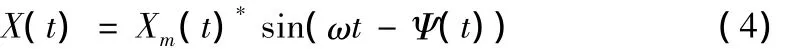
将其分解后，可以得到两个相互正交的正弦信号:

在式（5）中，令:

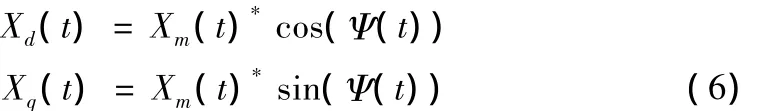
在上式中，Xd（t）和Xq（t）项包含了任意单相变量的幅值和相位信号，而这两个信号的变化是非常缓慢的，因此可以认为Xd（t）和Xq（t）是直流信号。因此，如果能够将这两项从相乘的正弦和余弦中分离出来，即对任意变量进行解耦，就可以将类似于在三相系统中使用的dq坐标变换应用到单相系统中。一种可行的解耦合策略，整个结构可分为三个部分，其控制流程如图4所示。首先，通过低通滤波器消除开关频率处的谐波量，其次，通过构造一个与网侧电流正交的虚拟电流向量，从而构成虚拟的两相静止坐标系，最后，对这个坐标系进行Park变换（二维正交变换矩阵），就可以得到Xd（t）和Xq（t）。为了构造出虚拟的两相静止坐标系，将实际的网侧电流X（t）延迟1/4周期，得到正交信号Y（t）的表达式为:

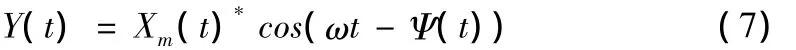
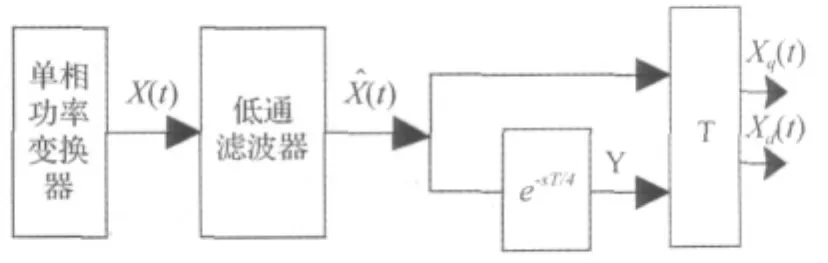
图4 虚拟静止坐标系下的DQ变换流程图

这样，{X（t），Y（t）}构成了两相虚拟正交αβ 坐 标系。设id、iq所在的{d，q}为旋转坐标系，且令d轴与网侧电压矢量US的方向保持一致，得出两坐标系间的关系如图5所示。很显然，x的dq轴分量是一个常数，θ是dq坐标系的旋转角度，可由（8）式表达:

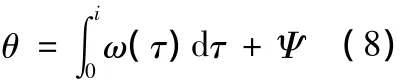
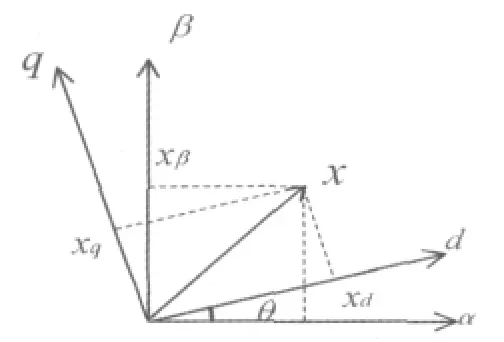
图5 静止坐标系与等效旋转坐标系

因此，单相系统等效的旋转变换矩阵（9）以及逆变换的矩阵（10）为:

逆变器输出电压状态变量的表达式如（11）所示，同时网侧电感电流也有类似的表达式。

单相并网逆变器的主要控制对象就是网侧电感的电流IL，由图2的单相并网逆变器原理图，假定直流母线的输出电压恒定，并且电路中无损耗，根据基尔霍夫电压定律可得，其中V（t）是逆变器输出电压:假定市电电压Vg（t）为参考角度，根据式（5）可将式（12）中各个变量的表达式改写为:

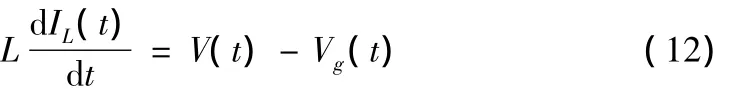
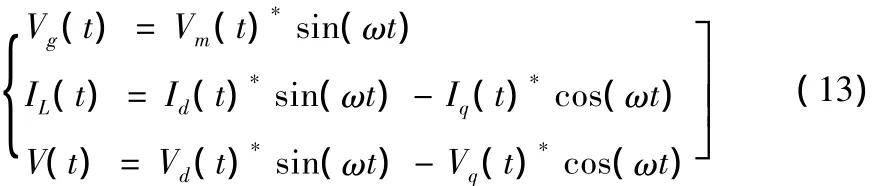
联合式（12）（13），可以得到与电感电流有关的系统特性方程（14）:

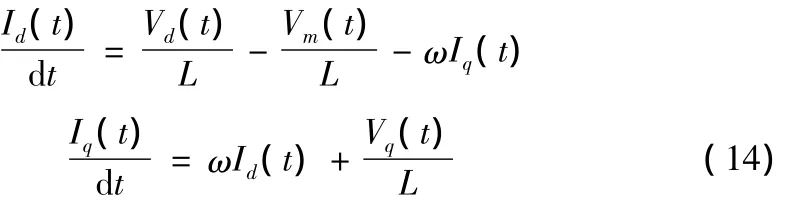
1.4 系统解耦控制

由单相并网逆变器的输出电流公式（1）可知，系统扰动主要源于电网，电网的扰动或者畸变会导致并网电流的畸变，为了进一步的提高并网电流的质量，引入前馈电压补偿，另外，从单相VSI的dq模型方程式（14）可以看出，由于VSI的d、q轴变量相互耦合，会给PCI控制器设计造成困难，采用前馈解耦合控制，系统的控制结构如图6所示。

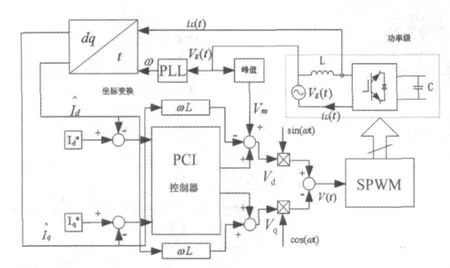
图6 PCI控制器的dq轴解耦合控制系统结构框图

2 仿真实例和实验结果分析

采用MATLAB/Simulink对PI和PCI+解耦合单相逆变器并网电流控制进行仿真研究。仿真参数如下:电网电压幅值155 V，工频50 Hz，直流母线电压360 V，给定电流峰值为19.34 A，系统的开关频率是 20 kHz，滤波电感 3 mH（0.01 Ω）。

对参数Kp，为保证系统具有较快的响应速度，同时避免放大噪声，系统带宽范围一般选择高于基波频率10倍且低于开关频率的1/5，根据带宽的定义，当系统闭环幅频特性的幅值降到3 dB时对应频率为ωb，0～ωb的频率范围称为系统的带宽［11］。考虑到Kp和Ki对闭环幅频特性的影响，本文选取系统的带宽fb=720 Hz，ωb=4 524 rad/s。因此，此系统的 Kp=0.15，Ki=25。

2.1 单相逆变系统PCI控制算法可行性验证

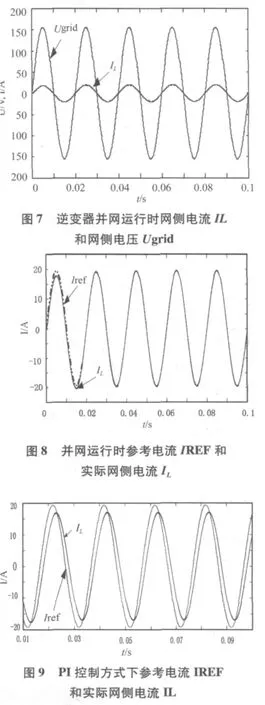
图7、8是单相并网逆变器PCI控制的并网仿真结果，其中包含了给定参考电流IREF、网侧电流IL和市电电压Ugrid。从图8可以看出，并网逆变器在经过一个工频周期的过渡过程之后稳定的并网发电，实际的并网电流IL能够无静差的跟踪给定的正弦参考电流IREF。同时，从图7看出并网电流和电网电压同频同相，逆变器能够实现单位功率因数的并网发电。证明了比例复数积分控制算法的可行性。

2.2 PCI和PI控制方式的稳态性能和抗干扰能力比较

由上文分析可知，常规的PI调节器跟踪交变的信号会存在误差，经过PI运算后输出的SPWM调制波会有比较严重的脉动，含有大量的谐波，因此，并网逆变器输出电流会与给定的参考电流产生较大的误差，同时含有谐波分量。图9分别是PI控制器下的参考电流和实际并网电流的误差结果，表明了实际运算中并网电流会产生幅值和相位的误差，调节Ki和Kp不能完全的消除这种误差。比较图8和图9，由仿真结果对比可以看出，在稳态时，PI控制、PCI+解耦控制下逆变器输出电流峰值分别为17.45 A和19.3 A，PCI控制方式下能够无静差的跟踪交流正弦信号。

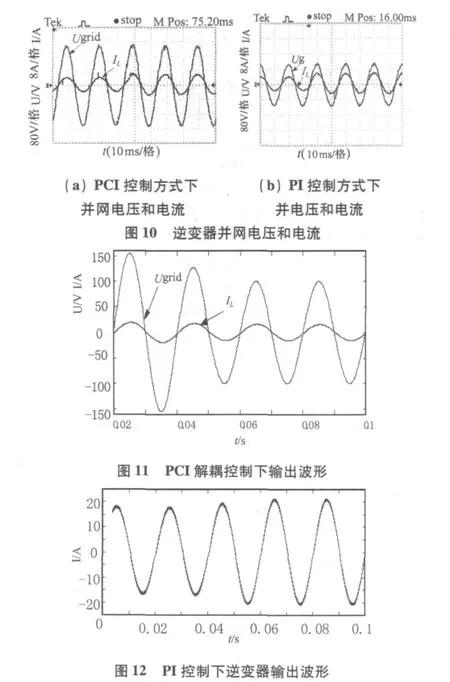
为了进一步的验证两种控制方式的稳态性能，研制了一台1 kW的试验样机进行了测试试验，样机的主要参数如下:直流输入电压400 V，滤波电感3 mH，采样频率 20 kHz。图10分别是两种控制方式下并网逆变器的试验波形。从两个波形对比同样可以得到与仿真同样的试验结论。

另一方面，仿真模拟电网电压有比较大的扰动（仿真时在0.04 s时电网电压突降到100 V），比较仿真结果图 11、12可知，并网电流总谐波畸变率（ηTHD）分 别 为3.87% 和 0.6%。PI控制下逆变器输出波形产生了较大的波形畸变，输出电流的FFT分析如图13所示，抗电网干扰能力较差，而在PCI解耦控制下，d－q轴电流是将交流量分解成为等效的直流量进行分开的控制，输出电流是正弦波而且没有严重的脉动现象，因此可以验证，后者应用于系统后，系统有更强的抗电网干扰能力。

3 结束语

本文将比例复数积分控制应用到单相并网逆变器，建立了单相系统在d－q旋转坐标系下的数学模型，通过理论分析并且对单相并网逆变器进行控制器仿真，与传统PI控制对比，验证了PCI解耦合控制有对交变信号零稳态误差跟踪和抗干扰性能。

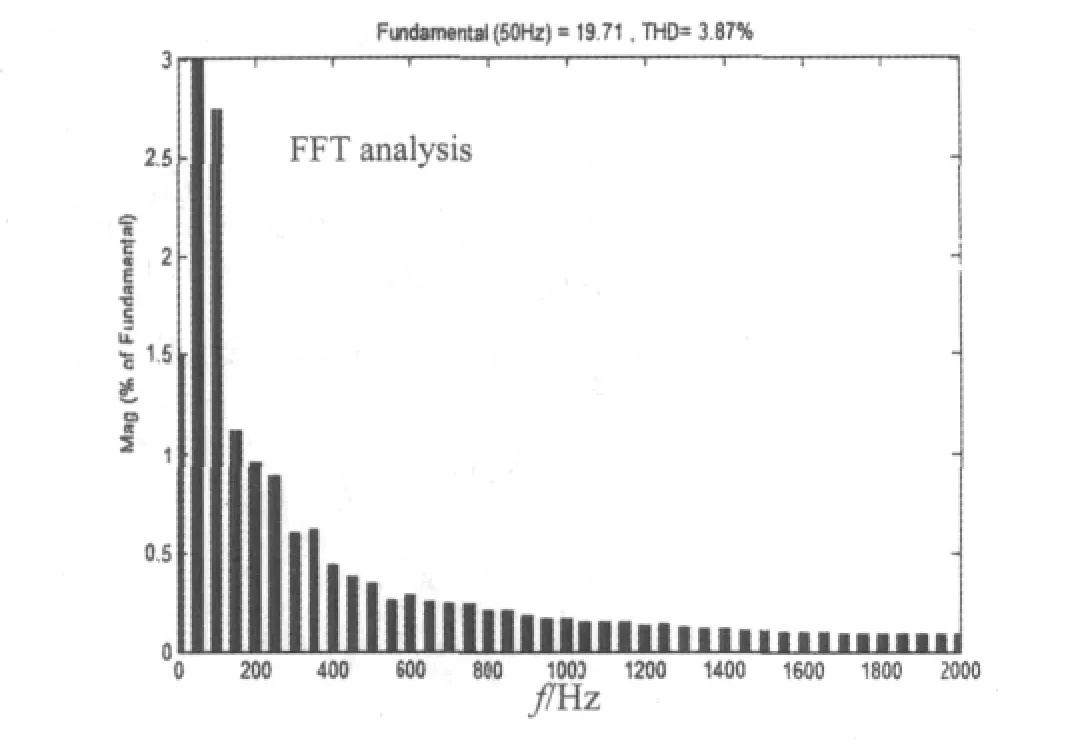
图13 PI控制方式输出电流的谐波分析

［1］赵为，太阳能光伏并网发电系统的研究［D］.合肥:合肥工业大学，2003.

［2］Chen Y M，Liu Y C，Hung S C.Multi－input inverter for grid－connected hybrid pv/wind power system［J］.IEEE Trans.on Power Electronics，2007，22（3）:1070 －1077.

［3］张强，张崇巍，张兴，等.风力发电用大功率并网逆变器研究［J］.中国电机工程学报，2007，27（16）:54 －59.

［4］ Infield D，Onions P，Simmons A，et al.Power quality from multiple grid －connected single-phase inverters［J］.IEEE Trans.on Power Delivery，2004，19（4）:1983 －1989.

［5］赵为，余世杰，沈玉梁，等.光伏并网发电系统的控制方法［J］.电工技术，2002，（3）:12 －13.

［6］唐欣，罗安，涂春鸣.基于递推积分PI的混合型有源电力滤波器电流控制［J］.中国电机工程学报，2003，23（10）:38 －41.

［7］粟时平，李圣怡.并联有源滤波器的最优电压滞环电流控制［J］.电力自动化设备，2002，22（4）:14 －17.

［8］ Boutot T，Chang L.Development of a single－phase inverter for small wind turbines:IEEE 1998 Canadian Conference on Electrical and Computer Engineering，Waterloo，May 24 －28，1998［C］.New York:IEEE Press，c1998.

［9］赵清林，郭小强，邬伟扬.单相逆变器并网控制技术研究［J］.中国电机工程学报，2007，27（16）:61 －64.

［10］郭小强，邬伟扬，等.三相并网逆变器比例复数积分电流控制技术［J］.中国电机工程学报，2009，29（15）:8 －14.

［11］刘健.电路分析［M］.北京:电子工业出版社，2006:210－212.