地下结构地震破坏静-动力耦合模拟研究

王 苏，路德春，杜修力

（北京工业大学 城市与工程安全减灾教育部重点实验室，北京 100124）

1 引 言

土是由土颗粒、孔隙水和孔隙气体组成的摩擦类材料，其力学特性不仅取决于土自身材料的组成成份，而且与荷载的作用密切相关，包括两方面，一是初始应力状态，一般为自然状态土的自重应力状态；二是附加荷载的应力路径[1]。相应地，土表现出两种基本力学特性，即压硬性和剪胀性，压硬性指土的抗剪强度和刚度随着约束压力的增大而增大；剪胀性指土在附加剪应力作用下产生体积膨胀或收缩的特性。

地下结构赋存于岩土介质中，其地震响应与地面结构的惯性效应不同，主要受围岩土体的变形控制。土体的变形取决于两部分荷载，一是地震作用的附加荷载；二是土体的自重应力。数值模拟时，土体的自重应力状态与地震荷载的静-动力耦合作用一般通过人工边界条件的设置实现，主要有3种方法：第1种方法为静-动力统一人工边界方法[2]，这种方法是在黏弹性动力人工边界的基础上，通过改变人工边界条件的刚度系数来实现静-动力耦合分析，但对刚度系数的改变尚缺乏明确的物理解释。第2种方法为动力松弛法[3]，该方法认为，土体的自重应力状态，是土体在阶跃荷载作用下从原始非受载状态发生振动达到平衡时的稳定状态。动力松弛法将静力问题看作动力问题的一部分，为阶跃载荷作用下动力响应的稳定状态，而不考虑动力过程。它的优点是避免了直接求解联立方程组，对任何系统都有确定的求解步骤，计算简单并便于程序实现。用于地下结构-围岩系统地震反应分析时，动力松弛法要求土体的本构模型适用于从非受载状态到地震荷载作用的全过程，目前还没有统一描述从小应变到大应变全范围的土的非线性本构模型[4]，若采用土的常规本构模型则不能合理地统一考虑土体的自重应力状态与地震荷载作用。第3种方法是首先进行静力分析，然后将静力分析得到的支座反力在静力分析步向动力分析步转化过程中，以集中力形式施加于侧向和底部边界面支座对应的单元节点上，以此作为动力分析的初始条件，实现静力边界条件与动力边界条件的统一。

本文将地下结构-围岩系统的静-动力耦合作用归结为考虑土体自重应力状态影响的地下结构-围岩系统地震响应问题，通过静力分析获得初始地应力，将其作为集中力作用于单元节点上，利用杜修力等[5－6]提出的应力型黏弹性人工边界条件，结合有限元分析软件ABAQUS，实现地下结构地震响应静-动力耦合模拟。利用本文的模拟方法，通过自定义的混凝土材料本构模型，将极限剪应变作为破坏标准，采用生死单元模拟地下结构的地震破坏过程，分析了结构埋深即土体的初始应力状态对其抗震性能的影响。

2 地震波垂直入射黏弹性人工边界

对近场波动问题进行数值分析，将未知的散射场或边界外行场用总场减去自由场或边界入射场（用上标i表示）表示，得到含外源作用的人工边界面l节点i方向的运动方程为[6]

式中：δij为克罗内克符号；ml为节点l的集中质量；klikj为节点k方向j对于节点l方向i的刚度系数；clikj为节点k方向j对于节点l方向i的阻尼系数；Al为人工边界面上l节点的影响面积；fli为入射地震波作用下l节点i方向的等效节点力；Fli为在结点l方向i处截去的无限远场对有限近场的作用力；式（2）括号内右边3项分别为克服弹簧、阻尼器及介质所需的抗力；对于三维问题，n=3，下标i和 j分别为1、2、3，分别对应于直角坐标系的x、y和z轴。Kli、Cli为l节点的人工边界弹簧和阻尼元件参数，如图1所示，对于三维人工边界，弹簧-阻尼元件参数为

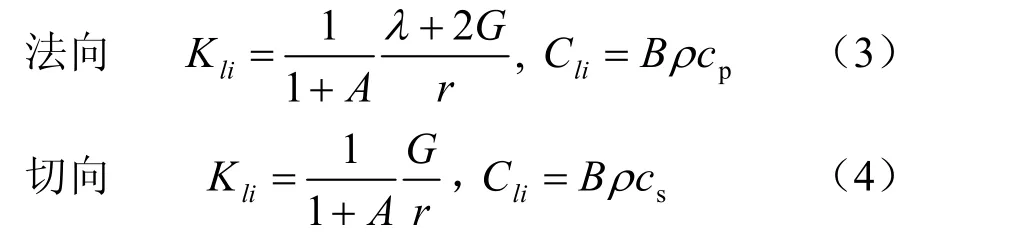
对于二维人工边界，弹簧-阻尼元件参数为

式中：λ为介质的拉梅常数；G为剪切模量；ρ为介质密度；cp和cs分别为P波和S波的波速；r为结构几何中心到该人工边界点所在边界线或面的距离；参数A和B的值分别建议为A=0.8，B=1.0。

图1 三维黏弹性人工边界Fig.1 Three-dimensional viscoelastic artificial boundary

3 静-动力耦合边界条件模拟方法

通过静力分析求得土体与结构各单元的内力及支座反力，将所得内力作为初始内力施加到各单元上，边界处采用黏弹性人工边界条件，并将静力分析得到的支座反力施加到黏弹性边界的节点上，再进行一次静力分析，此次所得结果便是地下结构-围岩系统的初始应力状态，并且无初始变形，通常称为地应力平衡。将初始地应力作为动力分析的初始状态，之后再进行地震响应分析，即可得到考虑土体初始自重应力状态影响的地下结构地震响应。

基于有限元分析软件 ABAQUS，编制了静-动力耦合人工边界模拟子程序，程序流程如图2所示。为验证本文提出的静-动力耦合边界模拟方法以及相应的子程序，采用数值算例进行验证。

图2 静-动力耦合人工边界施加流程图Fig.2 Flow chart of artificial boundary setting instatic-dynamic coupling

算例有限元模型如图3所示，土体区域为250 m×250 m×250 m，单元为10 m×10 m×10 m的六面体实体单元。土体的材料参数分别为，密度ρ=2 g/cm3，弹性模量E=117 MPa，泊松比υ=0.3，剪切波速cS=150 m/s。输入的脉冲为垂直入射S波，时间步长为0.005 s。位移与速度时程曲线如图4所示。

图3 有限元模型及黏弹性人工边界Fig.3 Finite element model and viscoelastic artificial boundary

图4 位移与速度时程曲线Fig.4 Displacement and velocity time histories

静力分析后自重应力达到了K0固结状态，竖向应力符合 σv=ρg z 关系，z为距地表的埋深；水平向应力符合 σh= K0σv关系， K0= υ (1 - υ)。图5为静力分析后土体的竖向位移云图，各位置处的竖向位移均小于在4×10-5m，该结果取决于土体的弹性模量E与柏松比υ，忽略图5所示的竖向固结变形对地下结构的地震反应对分析几乎无影响。图 6是采用黏弹性边界后土体底面和地表位移数值解与解析解的比较，表明本文设置的黏弹性边界条件可较好地模拟边界处的能量辐射，并实现地震动的输入。

图5 初始时刻土体竖向位移Fig.5 Vertical displacement of soil at initial time

图6 底边界与地表位移时程解析解与数值计算结果的比较Fig.6 Bottom boundary and surface displacement time analytical solutions and numerical calculation results

4 地下结构-围岩系统静-动力耦合模拟

地下结构的埋深不同，主要反映了结构埋深处土体的自重应力状态不同，埋深越深，土体的自重应力越大。本文分别模拟了结构顶板距地表的埋深为10、15、20 m共3个二维算例。地下结构-围岩系统有限元模型中，结构模型水平向长为20 m，高为6 m，内有2根截面宽为0.4 m的柱子，顶板及左右墙厚为0.4 m，底板厚为0.6 m；土体范围为结构两侧各为20 m，结构底板距计算区域下边界20 m，3个算例结构顶板距地表分别为10、15、20 m。土体单元网格为 1 m×1 m；结构大部分单元网格为0.3 m×0.2 m，局部细划，结构埋深10 m的有限元模型如图7所示。土体与结构均采用四面体实体单元，土-结构相互作用界面采用接触面对罚函数法，摩擦系数取0.6。

图7 地下结构-围岩系统数值计算模型Fig.7 Numerical calculation model of underground structure-rock system

地震动输入为修正后的 Kobe波，位移峰值与速度峰值均放大2倍，时间步长为0.005 s，输入的地震波只考虑水平x向SV波，位移时程和速度时程曲线如图8所示。

土体采用 Drucker-Prager本构模型，模型参数如表1所示。钢筋混凝土结构等效为均一材料，并基于ABAQUS自定义弹塑性损伤模型[7]，损伤因子D与等效塑性应变为指数关系，表达式为

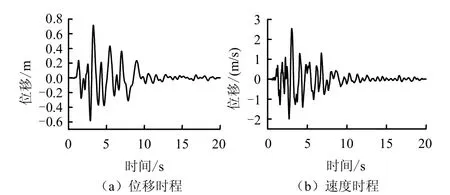
图8 地震动的位移时程与速度时程曲线Fig.8 Displacement and velocity time histories of seismic waves

表1 土的物理力学参数Table 1 Physical and mechanical parameters of soil

采用生死单元法模拟地下结构-围岩系统的地震响应。利用ωD作为单元删除的判断准则，ωD为随着损伤因子D单调增加的状态变量，表示单元的损伤程度，始终 ΔωD≥0，当ωD=1时，单元被“删除”。“删除”后的单元，其材料的变形模量趋于0，与未删除的相邻单元保持变形协调，位移连续。在有限元模型中对“删除”的单元进行隐藏，不进行网格重新划分，是一种假想的删除。数值模拟结果如图9～11所示，DUCTCRT即为ωD的值。

图9 埋深10 m时地下结构的地震破坏过程Fig.9 Earthquake failure process of underground structure with the depth of 10 m

图11 埋深20 m时地下结构的地震破坏过程Fig.11 Earthquake failure process of underground structure with the depth of 20 m

对于埋深10 m的结构，其地震破坏首先从中柱与底板的连接处开始，随着塑性应变的增大，损伤进一步积累，另一中柱与底板的连接处也开始破坏，最后是侧墙与底板连接处破坏。对于埋深15 m的结构，其地震破坏的规律与埋深10 m时相似，区别在于埋深15 m时结构破坏的时间整体早于埋深10 m时结构破坏的时间。对于埋深20 m的结构，其地震破坏同样首先从中柱与底板的连接处开始，然后是中柱与顶板的连接处破坏，最后是边墙与底板连接处、边墙与顶板连接处破坏，每一破坏处的破坏区域以及结构整体的破坏程度均显著大于埋深10 m和15 m时，结构地震破坏的时间与埋深10 m时接近。将3个埋深的地下结构破坏过程整理为图12，埋深15 m时的地下结构单元初始破坏的时刻在2.252 s，比埋深10 m和埋深20 m的地下结构单元初始破坏的时刻早，而且结构破坏的时刻也比另外两种埋深早，说明此地下结构形式，在地震作用下存在一个最不利埋深，在该埋深时结构最容易发生地震破坏。埋深20 m时的地下结构单元初始破坏的时刻最晚，表明地下结构埋深超过最不利埋深后，随着埋深的加深结构越不容易发生地震破坏；另一方面，埋深20 m时的地下结构中柱与顶板的连接处以及侧墙与顶板的连接处均发生了地震破坏，表明深埋地下结构一旦发生地震破坏，其破坏程度随着埋深的加深而加重。

图12 不同埋深时结构的地震破坏过程Fig.12 Seismic damage process of structure at different buried depths

5 结 论

本文从土的力学特性分析入手，将荷载作用分为自重荷载与附加荷载两部分，并将自重应力作为附加荷载作用的初始状态，该思路与当前研究土的力学特性与本构模型的建模方法一致。进而将地下结构-围岩系统的静-动力耦合作用归结为考虑土体自重应力状态影响的地下结构-围岩系统地震响应问题，分别进行静力与动力分析，通过人工边界条件的设置实现了地下结构地震响应静-动力耦合模拟。

（1）本文提出的土体自重应力的分析思路以及相应的人工边界条件的设置方法，为地下结构的抗震性能分析与评价提供了一种有利工具。

（2）初始地应力显著地影响地下结构-围岩系统的动力响应，地下结构对于抗震性能而言存在一个最不利埋深，处于最不利埋深时最容易发生地震破坏；埋深超过最不利埋深时，埋深越深地下结果越不容易发生地震破坏，一旦发生地震破坏，结构的埋深越深，其地震破坏的程度越重。

[1]路德春, 姚仰平. 砂土的应力路径本构模型[J]. 力学学报, 2005, 37(4): 451－459.LU De-chun, YAO Yang-ping. Constitutive model of sand considering complex stress paths[J]. Acta Mechanica Sinica, 2005, 37(4): 451－459.

[2]刘晶波, 李彬. 三维黏弹性静-动力统一人工边界[J].中国科学: E 辑, 2005, 35(9): 966－980.LIU Jing-bo, LI Bin. 3D viscoelastic static-dynamic artificial boundary[J]. Science in China: Serial E, 2005,35(9): 966－980.

[3]杜修力. 工程波动理论和方法[M]. 北京: 科学出版社,2009.

[4]PAPADIMITRIOU A G, BOUCKOVALAS G D.Plasticity model for sand under small and large cyclic strains: A multiaxial formulation[J]. Soil Dynamics and Earthquake Engineering, 2002, 22(3): 191－204.

[5]杜修力, 赵密, 王进廷. 近场波动模拟的一种应力边界条件[J]. 力学学报, 2006, 38(1): 49－56.DU Xiu-li, ZHAO Mi, WANG Jin-ting. A stress artificial boundary in FEA for near-field wave problem[J]. Acta Mechanica Sinica, 2006, 38(1): 49－56.

[6]杜修力. 局部解耦的时域波分析方法[J]. 世界地震工程, 2000, 16(3): 22－26.DU Xiu-li. A partially decoupling analytical method for wave propagation problems in time domain[J]. World Information on Earthquake Engineering, 2000, 16(3):22－26.

[7]王苏. 地下结构地震破坏过程弹塑性模拟研究[D]. 北京: 北京工业大学, 2012.