组合模型在风电场发电功率短期预测中的应用

牛晨光，游晓科，刘观起，赵振云

(1.华北电力大学 电气与电子工程学院，河北 保定 071003;2.河北省电力公司，河北 石家庄 050000)

0 引言

近年来，世界风电产业迅猛发展，2010年世界各地累计新增风电装机容量将近36 GW。中国作为世界上最大的发展中国家，其风电装机容量增速持续超过100%，已经成为全球风电产业之首[1，2]。然而，风电具有随机性、间歇性和不可控制的特点。当前的风电比例较小，电网还有能力应对，但随着风能规模的不断扩大，电网的主动性将逐步降低，因此，为了尽可能减少由于风电接入对系统调峰容量的增量需求，提高电网运行的经济性及电网接纳风电的能力，必须将风电功率预测作为未来电力系统建设的重要组成部分，不断提高预测精度。

目前，风电场发电功率短期预测还处于起步阶段，采用的模型基本可以分为线性预测模型和非线性模型，而且大都只是针对单项模型进行研究[3，4]，很少对各单项预测模型联系起来。本文采用支持向量机法和神经网络法，通过对各单项模型的预测结果对比分析，建立基于最小方差的组合预测模型，以达到提高预测准确度的目的。

1 支持向量机模型

1.1 支持向量机模型基本原理

对于样本 (x1，y1)， (x2，y2)，…， (x1，y1)，首先在样本与特征空间φ(xi)之间建立一个非线性映射φ(.)，在这个高维特征空间中构造最优决策函数，

这样就把非线性估计函数转化为高维特征空间的线性估计函数;然后根据结构风险最小化原则，寻找ω，b的最小化。常用的最小二乘支持向量机的优化目标函数为误差ξi的二次项，故优化问题为[3]

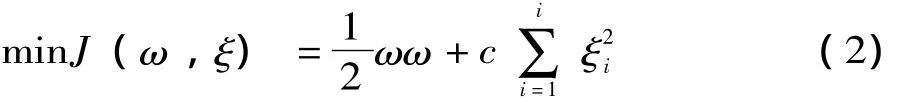
s.t.yi=ωφ (xi)+b+ξi(i=1，2，…，l)

用拉格朗日求解该问题，有

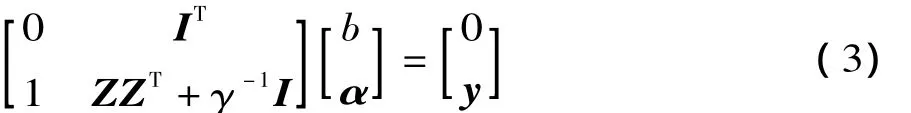
1.2 实例分析

该风电场配备了数值气象预报系统，采用数值气象预报系统数据进行预测，但由于该系统刚刚投入运行，数据数量有限。采集其中的风速、温度、风向余弦值、气压数据，这样做主要是因为考虑到预测时刻的这些数据对该时刻的功率产生较大的影响。

将2010年6月17日到2010年6月25日的风速、温度、风向余弦值、气压数据作为训练样本，2010年6月17日到2010年6月25日的功率作为训练目标，基于 MATLAB7.6平台，运用LSSVM工具箱1.5 b版本，完成对数据样本的训练以及预测，以2010年6月27日的数值气象预报数据作为输入，预测该日的功率数据。

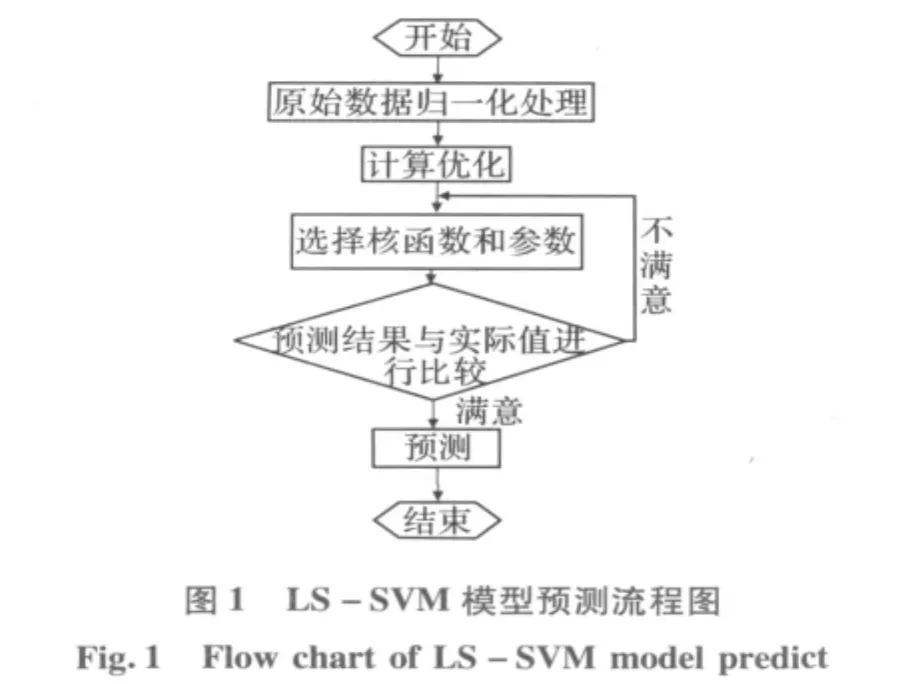
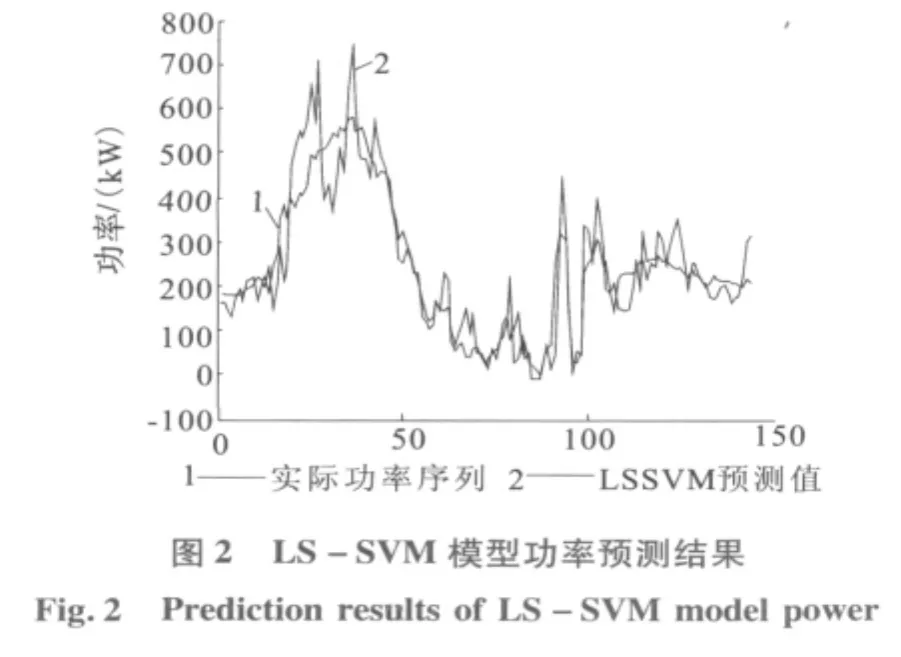
预测流程图如图1所示。预测结果如图2所示。该种方法预测的均方根误差和百分比误差分别为67.282 0和0.040 4。

2 基于相空间重构的RBF神经网络模型

2.1 相空间重构理论

风电功率的历史时间序列数据本身包含丰富的气象、地理信息，而这些气象信息介于随机与规律之间，明显具有混沌属性，而且混沌系统运动在短期内轨道发散较小，是可预测的[5]。

根据Takens的嵌入定理[5]，混沌系统中任一分量的演化都是由与之相互作用着的其他分量所决定的。因此，系统相空间的重构只需考虑一个分量，通过某些固定的延时点上的观测值找到一个m维向量，就可以重构出一个等价的相空间。对于混沌时间序列x1，x2，x3，…，xn-1，xn，若嵌入维数为m，延迟时间为τ，则相空间重构为:

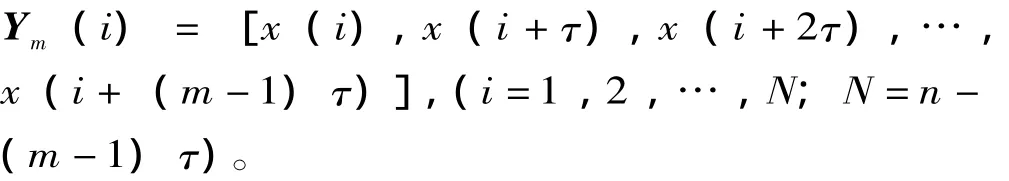
在相空间重构过程中，恰当地选取嵌入维数和延迟时间，可以提高相空间重构的质量，进而提高预测的精度。

(1)互信息求嵌入维数[6]

互信息来源于信息论，描叙2个随机变量间的随机关联度量。是一种非线性方法，用来分析混沌时间序列是一种合理的方法。其基本思想是，选取互信息函数第一次达到局部极小值的τ作为最佳延迟时间。

2 组信号{x(i)，y(j)}(i=1，2，…，N;j=1，2，…，N)，给定x(i)的一个测量值，预测y(j)的平均信息量为互信息函数:

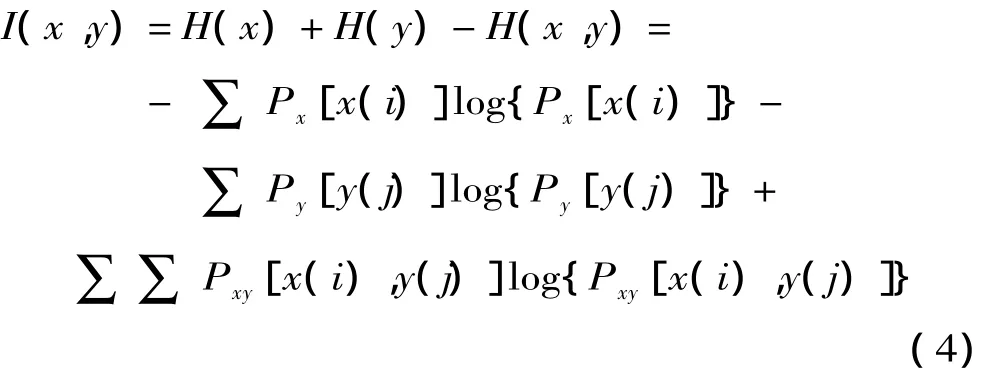
式中:H(x)为信号 {x(i)}的熵，表示对指定系统的N个x(i)测量得到的平均信息量，信息熵越大，不确定性越强;H(y)的定义与H(x)类似;H(x，y)为联合信息熵。互信息函数I(x，y)的大小反应的是 {x(i)}，{y(j)}之间的相关性的强弱。

(2)Cao算法求取潜入维数[7]

对于混沌时间序列x1，x2，x3，…，xn-1，xn，若嵌入维数为m，延迟时间为τ，则相空间重构如式 (1)所示。

定义判据

α(i，m)=

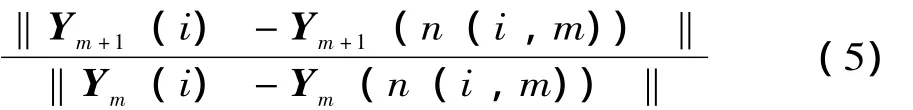
式中:Ym+1(n(i，m))为相点矢量 Ym+1(i)的邻近点，Ym(n(i，m))是相点矢量Ym(i)的邻近点。Cao算法又引入E1(m)和E2(m)作为判据:

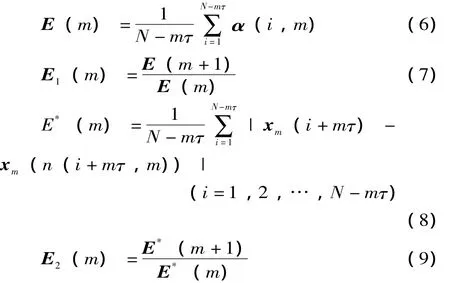
2.2 实例分析

在时间序列重构问题中，求的是x(t+τ)值对x(t)值的依赖性，因此，令 (x，y)=[x(t)，x(t+τ)]。对于某风电系统，随机选择其2010年30天的发电功率时间序列，每隔10 min提取其中4 320个功率数据构成一时间序列，互信息函数I(x，y)与时间延迟τ的变化关系如图3所示。由图可知，时间延迟取19。

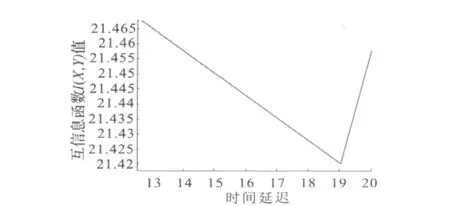
图3 互信息函数I(X，Y)与时间延迟τ关系Fig.3 Relationship of mutual information function I(X，Y)and time delay τ

对该风电功率时间序列，利用Cao算法得到的E1(m)和E2(m)与嵌入维数m的关系如图4所示。从图4中可以看出E2(m)在1附近振荡，说明该时间序列含有确定性成分;而当嵌入维数增加到12时，E1(m)趋于稳定。因此选嵌入维数为12。

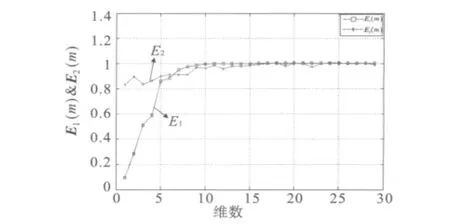
图4 E1(m)和E2(m)与嵌入维数m的关系Fig.4 Relationship of E1(m)and E2(m)resepectvely with the Embedded dimension m

工程实际中，如果一个系统是混沌，则至少存在一个正的Lyapunov指数，反映了轨道从初始条件附近开始发散的速度。因此，可以通过估计系统的最大Lyapunov指数，来判断系统的混沌属性。其最大Lyapunov指数为0.041 3，大于0，说明该时间序列具有混沌属性。

根据上述分析，基于RBF神经网络模型进行功率预测[8]，其输入节点数取为嵌入维数12，进行单步预测，预测未来24 h功率，即144个点。其预测结果如图5所示。其均方根误差和相对误差分别为53.846 7和0.034 8。由此证明基于相空间重构的RBF神经网络预测模型能够得到较高的预测精度，可以满足生产现场实际的需要。

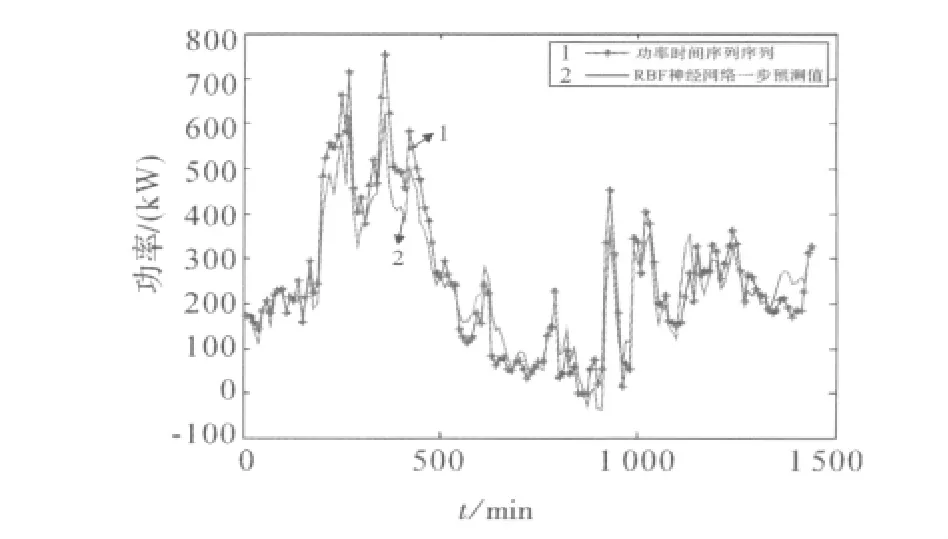
图5 RBF神经网络模型预测结果Fig.5 Results of RBF neural network forecasting

3 组合预测模型

Bates和Granger于1969年首次提出组合预测的概念，即综合考虑各单项预测方法的特点，将不同的单项预测方法进行组合，综合利用各种预测方法所提供的信息，以适当的加权平均形式得出组合预测模型[3]。组合预测模型最关心的问题就是如何求出加权平均系数。本文使用最小方差法[9]进行组合加权平均系数的求取。

设第i种单项预测方法的预测误差为ei，方差为Var(ei)，组合预测模型的误差为e，方差为Var(e)。则有

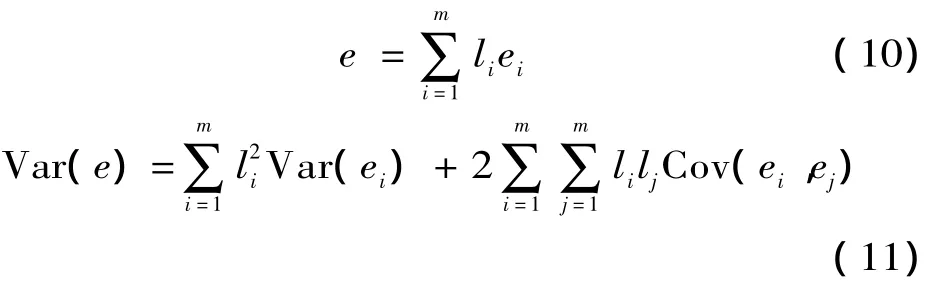
式中:Cov(ei，ej)为ei，ej的协方差。以最小方差为优化目标，求解各种方法的权重系数为

设基于混沌理论的RBF神经网络法的误差为eRBF，权系数为lRBF;LS-SVM模型的误差为eLSSVM，权系数为 lLSSVM。经过编程计算，确定 lRBF=0.697 3，lLSSVM=0.302 7。预测结果如图6所示。均方根误差和相对误差对比如表1所示。结果显示，组合预测法的预测结果较各单项预测法的结果精度上有了提高，更适用于工程实际。

图6 组合预测模型功率预测结果Fig.6 Results of power forecasting of combination forecast model

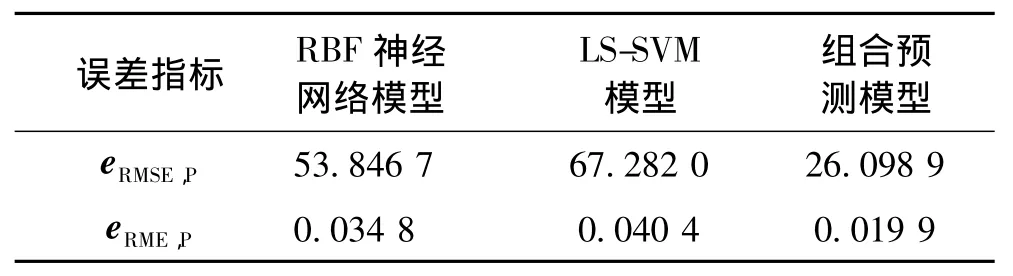
表1 组合预测模型与单项预测模型结果对比Tab.1 Results comparison of combination forecasting model and single forecasting model

4 结论

本文首先建立了LS-SVM模型，然后提出了一种基于相空间重构的神经网络功率预测模型，利用功率时间序列的混沌属性，还原其相空间结构的规律性，达到了提高预测准确度的要求。在此基础上，建立了组合预测模型。应用某风电场实地采集数据，对该文所提方法进行了验证，结果表明，组合预测可以提高预测的准确度，满足工程实际要求。

[1]The World Wind Energy Association.Half-year Report 2011[EB/OL].http://www.wwindea.org，2011-10.

[2]中国可再生能源学会风能专业委员会.2010年中国风电装机容量统计[EB/OL].http://www.cres.org.cn，2011-3.

[3]牛东晓，曹树华.电力负荷预测技术及其应用[M].北京:中国电力出版社，2006.

[4]姜勇.电力系统中短期负荷预测方法[J].电力科学与工程，2002，(4):8-11.Jiang Yong.Medium-short term load forecasting methods in electric power systems[J].Electric Power Science and Engineering，2002，(4):8-11.

[5]韩敏.混沌时间序列预测理论与方法[M].北京:中国水利水电出版社，2007.

[6]Abarbanel H D I，Masuda N，Rabinovich M I，Tumer E Distribution of mutual information.Physics Letters A，2001，281(5-6):369-373.

[7]Cao L.Practical method for determining the minimum embedding dimension of a scalar time series[J].Physica D:Nonlinear Phenomena，1997，110(1):43-50.

[8]傅荟璇，赵红.MATLAB神经网络应用设计[M].北京:机械工业出版社，2010.

[9]张国强，张伯明.基于组合预测的风电场风速及风电机功率预测[J].电力系统自动化，2009，33(18):92-95.Zhang Guoqiang，Zhang Boming.Wind speed and wind turbine output forecast based on combination method[J].Automation of Electric Power Systems，2009，33(18):92-95.