风切变指数的确定对风电场风速推算的影响分析

李 鹏，冯长青，韩小平

(1.内蒙古送变电有限责任公司，内蒙 呼和浩特 010020;2.内蒙古电力勘测设计院，内蒙古 呼和浩特 010020)

0 引言

风力发电是可再生能源形式之一，对于节约能源、保护环境和促进发展具有重要作用[1]。随着科学技术的不断进步，大规模开发利用风能资源已成为可能。风电场就是应用现代科学技术大规模利用风能的一种方式，而风能资源评估是整个风电场建设、运行的重要环节，是风电项目的根本，对风能资源的正确评估是风电场建设取得良好经济效益的关键。在对风电场进行风能资源评估时，主要是选择风电场内具有代表性的测风塔的测风数据，对其各个高度的风速、风功率密度、风向和风能频率以及湍流强度、风切变指数等风资源指标进行分析计算，其目的是选出适宜该风电场的合适机型和安装高度，以充分利用风能资源，降低投资成本，取得更好的经济效益。

风速随高度的增加将有显著变化，但由于地球表面粗糙度不同，风速随高度的变化也不同，有些地区风速随高度增加明显，而有些地区受地形等因素的影响风速随高度增加不明显，不同高度增加的程度也不同，越到高空变化越小，这种风速随高度的变化服从普朗特经验公式。在风电场资源评估中，就是根据普朗特经验公式推导出的风切变指数关系式分析风速随高度的变化情况。由于风电机组塔筒价格的变化对风机不同轮毂高度的动态收益会有显著的变化，所以在风能资源评估时对轮毂高度的选择是很关键的，有的风电场建设因风能资源评价失误，建成的风电场达不到预期的发电量，造成很大的经济损失。所以本文以内蒙古的两个风电场为例，分析风切变指数在风电场风速推算中的影响。

1 风电场地理位置及测风塔概况

本文所选的2个风电场都在内蒙古自治区鄂尔多斯市杭锦旗境内，2个风电场相距18 km。1号风电场中心坐标为东经107°34'16″，北纬40°08'22″，风电场占地面积约14 km2，海拔高程约为1 194～1 232 m，风电场内植被稀疏，地势较平坦，大部分为荒漠草原。2号风电场中心坐标为东经107°21'39″，北纬 40°11'40″，风电场占地面积约13 km2，海拔高程约为1 223～1 263 m，风电场内植被稀疏，地势较平坦，大部分为荒漠草原。

2个风电场内分别设有一个测风塔，其中1号测风塔位1号风电场内，2号测风塔位于2号风电场内，1号测风塔位于2号塔东南方向约17 km处，2座测风塔及与风电场相对位置见图1。测风塔测风设备均采用美国赛风Nomad2，所处地形地貌相似，且2座测风塔高度和风速仪安装高度相同，测风时段也相同，具体情况见表1。

图1 2座测风塔与风电场相对位置示意图Fig.1 Position map of two masts and wind farms

表1 测风塔位置及配置Tab.1 Masts position and equipment

2 不合理数据的验证

根据GB/T18710-2002标准，对测风塔主要参数进行合理性分析，经统计计算1号、2号测风塔的有效数据完整率都在97.0%以上，满足GB/T18710-2002《风电场风能资源评估方法》中有效数据完整率应在90%以上的要求。根据GB/T18710-2002标准，对不合理数据再次进行判别，挑出符合实际情况的有效数据，回归原始数据组。根据测风塔的相关关系以及可供参考的传感器同期记录数据，经过分析、处理、替换，整理出测风塔连续一年的实测风速风向数据，使其有效数据完整率达到100%。

3 风切变指数的计算方法及结果分析

3.1 风切变指数的定义

在近地层中，风速随高度有显著的变化，记录表明，在0.25 s内，风速可以由27 m/s突变到37 m/s[2]。造成风在近地层中垂直变化的原因有动力因素和热力因素，前者主要来源于地面的摩擦效应，即地面的粗糙度，后者主要表现为与近地层大气垂直稳定度的关系。当大气层结为中性时，湍流将完全依靠动力原因来发展，这时风速随高度变化服从普朗特经验公式[3]:

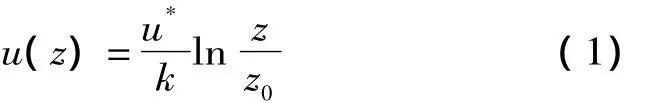
式中:u*为摩擦速度;k=0.4为von Karman常数。摩擦速度定义为u*=(τ/ρ)1/2，其中τ为表面剪切应力;ρ为空气密度。

假设混合长度随高度变化有简单指数关系，由此推导的风切变指数律[3]为:

式中:un和ui分别为高度在zn和zi处的风速;α即为风切变指数。

3.2 风切变指数的计算方法及结果分析

风资源评价中，风切变指数是涉及风力机安全的一个重要参数[4，5]，风力机的设计和选型都要考虑风切变指数的大小[6]，风电场轮毂高度的确定也要利用风资源数据计算得出的风切变指数进行分析评价。由于目前大多数风电场测风塔的安装高度为70 m，即风速仪的安装高度在10～70 m之间。而且风速仪的安转个数是有限的，一般只选择有代表性的几个高度，而风电机组的轮毂高度并不一定就是测风仪的安装高度，所以要根据现有的测风数据并利用计算所得的风切变指数，判断风速随高度的变化情况，选出合适的轮毂高度并推算风电机组实际安装高度处的风速进行风资源的评估论证。但由于地形因素等的影响，风流过时，某些高度层的风速会加速，将改变风廓线的形状，进而影响不同高度的风切变指数，所以，风切变指数的计算结果不同，对某些高层风速的评价结果将不同。本文采用以下4种方法计算风切变指数，探讨各方法的计算结果对不同高度风速变化的影响分析。

(1)采用全部数据计算风切变指数

如果测风塔数据完整率高，没有数据缺测现象，可采用全部数据计算风切变。计算方法为:将全部数据按不同测风高度，在每一测风时间点，利用指数关系式进行不同高度间的风切变指数计算。两测风塔各相邻高度间风切变指数计算结果的平均值见表2。

表2 全部数据在不同相邻高度间风切变指数计算结果的平均值Tab.2 Average value of wind shear exponent in different adjacent height calculated from the all data

由表2的计算结果可以看出，1号风电场10～30 m风切变很小，随着高度的增加风切变值逐渐增大，之后又逐渐减小。在50～60 m切变值最大，50～70 m切变值又减小，而60～70 m切变已经表现为负值，这说明1号风电场60～70 m风速随高度的增加已无明显变化。2号风电场各相邻高度间风切变指数的变化规律与1号风电场相同，但2号风电场10～30 m风切变值高于1号风电场10～30 m风切变值，到60～70 m风速随高度的增加变化很小。由此计算结果分析，本风电场60 m以上风速随高度的增加已不明显，建议风电机组轮毂高度不宜选择60 m以上的高度。

(2)去除3 m/s以下风速后计算风切变指数

风机的切入风速一般在3～4 m/s，3 m/s以下风速对风机功率没有贡献，且在小风速下，数据误差大。该方法是:去除3 m/s以下风速，在剩余每一测风时间点，利用指数关系式进行不同高度间的风切变计算。两测风塔各相邻高度间风切变指数计算结果的平均值见表3。

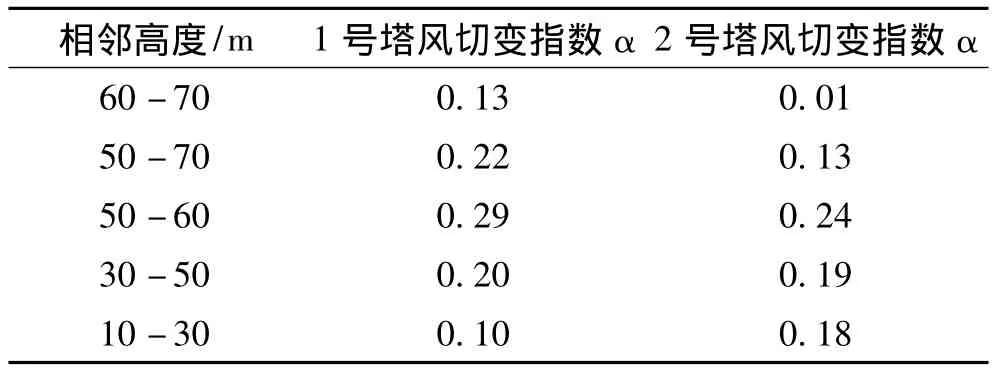
表3 去除3 m/s以下风速风切变指数计算结果的平均值Tab.3 Average value of wind shear exponent in different adjacent height calculated from the all data without wind speeds less than 3 m/s

由表3的计算结果可以看出，1号风电场各相邻高度间风切变指数的变化规律与方法1中计算结果的变化规律一致，但不同的是10～30 m和60～70 m风切变值明显高于方法1中的计算结果，而50～60 m的切变值低于方法1中的结果，原因是对数据进行筛选的结果，说明在10～30 m和60～70 m在3 m/s以下风速存在的数量较多，对其进行去除后导致了计算结果的偏大。2号风电场各相邻高度间风切变指数的变化规律与方法1中计算结果的变化规律一致，而且数值很接近。

(3)取平均风速后计算风切变指数

该计算方法为:将各个高度完整一年的数据，分别计算各个高度的平均风速，根据平均风速计算结果利用指数关系式进行不同高度间的风切变计算。两测风塔各相邻高度间风切变指数计算结果见表4。

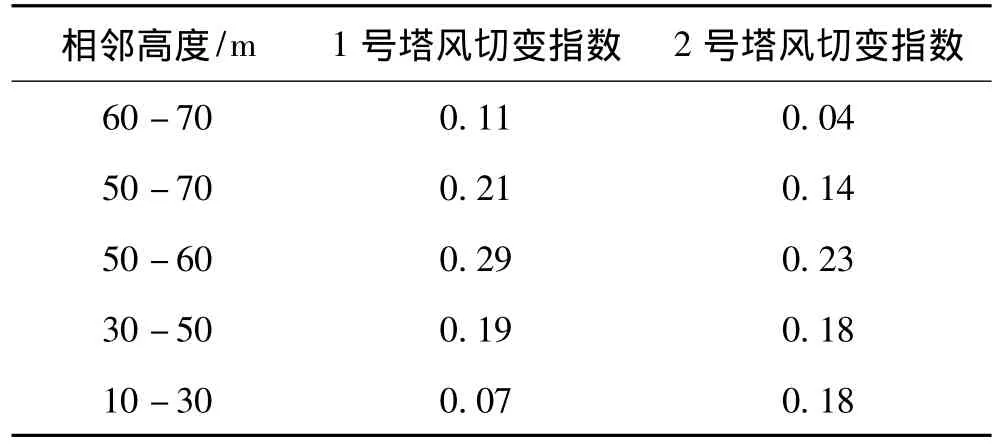
表4 用平均风速风计算的风切变指数值Tab.4 Wind shear exponent in different adjacent height calculated from average wind speeds

由表4的计算结果可以看出，1号风电场各相邻高度间风切变指数的变化规律与方法1、方法2中计算结果的变化规律一致，但不同的是60～70 m风切变值接近方法2中的结果而明显高于方法1中的结果，10～30 m风切变值低于方法2中的结果而明显高于方法1中的结果，其它各相邻高度间的切变值较接近。2号风电场各相邻高度间风切变指数的变化规律与方法1和方法2中计算结果的变化规律一致，而且数值很接近。

(4)通过风廓线计算风切变指数

该计算方法为:将各个高度完整一年的数据，分别计算各个高度的平均风速，根据不同高度绘制散点图，然后根据指数关系进行曲线拟合，得到风切变指数拟和曲线，结果见图2。

图2 两塔完整一年数据风切变指数拟合曲线Fig.2 Curve of wind shear exponent at two masts in a complete year

由图2可以看出，此方法只能拟合出一个均值。在1号风电场中，该拟合值与方法2中计算的60～70 m风切变值相同，与方法3计算的60～70 m风切变值接近。在2号风电场中，此方法的拟合值与前3种方法计算的10～30 m风切变值相同，与方法1和2计算的30～50 m风切变值接近，而与方法3计算的30～50 m风切变值相同。

从以上4种方法的计算结果可以看出，1号风电场采用不同方法计算的各相邻高度的风切变值在10～30 m和60～70 m差别较大，其他高度间差别较小，而2号风电场采用不同方法计算的相邻高度的风切变值相同或很接近。这说明两风电场虽然地形条件相似，但由于地面粗糙度、地形变化等因素的影响，风流过时，某些高度层的风速会加速，将改变风廓线的形状，进而影响不同高度的风切变指数值。对于本文中的2号风电场，4种方法计算的切变指数值在相同高度层相同或很接近;而1号风电场，4种方法计算的切变指数值在某些相同高度层存在很大的差别，所以应针对该风电场的实际情况，多方案比较后选择较合适的风切变计算值进行风资源的推算及评估论证。

4 不同风切变指数对风速推算的影响分析

假定风电场测风塔没有60 m高度，采用前面4种方法计算得出50～70 m的风切变指数推算60 m高风速，并与60 m实测风速进行比较分析，探讨各计算方法的误差情况。计算结果见表5和表6。

表5 1号塔60 m高实测值与推算值的比较Tab.5 Actual value and calculated value at No.1 mast on the height of 60 m

表6 2号塔60 m高实测值与推算值比较Tab.6 Actual value and calculated value at No.2 mast on the height of 60 m

从表5可以看出，1号风电场4种计算方法中误差最大的是方法4，其它3种方法推算结果的误差情况较小且很相近。原因是方法1～方法3计算的50～70 m切变值很接近，方法4拟合结果低于其他3种方法计算的50～70 m切变值，而更低于50～60 m切变值，所以导致方法4推算60 m高度风速的结果偏差较大。

从表6可以看出，2号风电场4种计算方法中误差最小的是方法4，其他3种方法推算结果的误差情况相近。原因是方法1～方法3计算的50～70 m切变值很接近，方法4拟合的结果高于其他3种方法计算的50～70 m切变值，而比其他方法计算结果更接近50～60 m切变值，所以方法4推算60 m高度风速的结果偏差较小。从以上分析可以看出，方法4拟合得出的风切变指数值并不能代表所有高度层风速的变化情况，在不同的风电场，该方法的计算结果与不同高度间的切变值存在的偏差是不同的。

5 结论与建议

(1)在不同的地区，或相同地区不同的风场，由于地面粗糙度、地形变化等因素的影响，风流过时，某些高度层的风速会发生改变，将改变风廓线的形状，进而影响不同高度的风切变指数，即使是相同的数据采用不同方法计算的风切变值也会有一定的差别。

(2)从风切变角度分析风速随高度的变化具有一定的参考价值，但在利用风切变指数值推算风电场某一高度的风速时，应结合风电场的实际情况进行多方法比较，选择适合本风电场的风切变指数计算方法，进行各高度风速的推算及风资源的评估论证。

(3)由于塔筒价格的变化对不同轮毂高度的动态收益会有显著的变化，建议在确定风电机组轮毂高度时，除参考风切变对各高度风资源的影响外，还可以通过详细的技术经济比选确定合适的高度。

[1]王兴武，高叔开，张照彦.基于STAR-90风力发电场仿真系统研制[J].电力科学与工程，2009，25(11):1-5，11.Wang Xingwu，Gao Shukai，Zhang Zhaoyan.Research and develop of wind power farm simulation system based on STAR-90[J].Electric Power Science and Engineering，2009，25(11):1-5，11.

[2]张礼达，陈荣盛，张彦南，等.风力机风轮叶片振动特性分析[J].电力科学与工程，2009，25(11):24-27.Zhang Lida，Chen Rongsheng，Zhang Yannan，et al.Study on wind turbine rotor blades dynamic characteristics based on ANSYS[J].Electric Power Science and Engineering，2009，25(11):24-27.

[3]王承煦，张源.风力发电[M].北京:中国电力出版社，2003.

[4]贺德馨，陈坤，张亮亮，等.风工程与工业空气动力学[M].北京:国防工业出版社，2006.

[5]Burton T，Sharpe D，Jenkins N，et al.风能技术[M].武鑫，译.北京:科学出版社，2007.

[6]廖明夫，徐可，吴斌，等.风切变对风力机功率的影响[J].沈阳工业大学学报，2008，30(2):163-167.Liao Mingfu，Xu Ke，Wu Bin，et al.Effect of wind shear on wind turbine power[J].Journal of Shenyang University of Technolgy，2008，30(2):163-167.