圆盘泵叶轮结构参数正交优化分析

王少平，高本金，尹树孟，周昌静

（1．中海油基地集团油田建设工程公司，天津300000；2．中国石油大学（华东）海洋油气装备与安全技术研究中心，山东青岛266580）

圆盘泵叶轮结构参数正交优化分析

王少平1，高本金2，尹树孟2，周昌静2

（1．中海油基地集团油田建设工程公司，天津300000；2．中国石油大学（华东）海洋油气装备与安全技术研究中心，山东青岛266580）

针对圆盘泵叶轮结构特点，利用FLUENT系统建立圆盘泵流体动力学分析模型，针对部分结构特征参数实现参数化建模。以获得最大压升为目标，分别对影响圆盘泵最大压升的单因素及多因素组合进行分析。针对多因素制定5因素4水平正交试验表，并对16种结构分别进行流体动力学计算仿真，得到影响圆盘泵最大压升因素的主次顺序及优化方案。为圆盘泵的设计提供参考。

：圆盘泵；FLUENT；正交试验；数值模拟

圆盘泵是一种离心式旋转机械，由Sargent于1850年发明，由Ntkola Tesla进一步研究并发展。最初设计的工作叶轮是1组圆盘，结构如图1所示，主要靠旋转圆盘及液体之间的摩擦力进行能量传递。因为过流部件表面的边界层效应，使其流体介质与叶轮表面相对速度较小而形成保护层，且叶轮中间存在无叶区，从而可以最大程度地减小被输送介质与过流部件的接触，降低圆盘叶轮表面冲击和摩擦，保证圆盘叶轮具有较长的工作寿命和可靠性。圆盘泵特别适用于输送含固体颗粒的流体介质。

由于叶片泵理论与实践的快速发展，圆盘泵不再受到重视。20世纪60年代，化学工业工艺流程有了新的进步，高粘度石油矿藏的开发以及造船工业的发展，给圆盘泵的发展带来了新的机遇。1970年，美国人Max I．Gurth在圆盘泵的试验方面获得极大成功，申请多项专利，并于1982年成立Discflo公司，专注生产圆盘泵。1988年，通过试验研制成功了高扬程圆盘泵，扬程得到极大提高，使圆盘泵应用得到极大推广。高扬程圆盘泵叶轮结构如图2所示［1－6］。

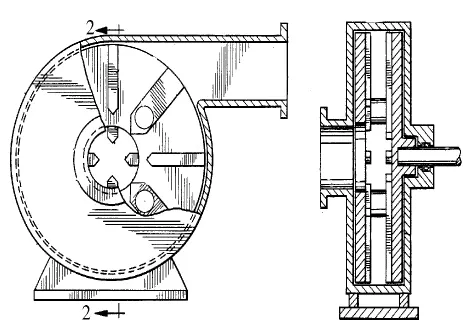
图1 圆盘泵结构

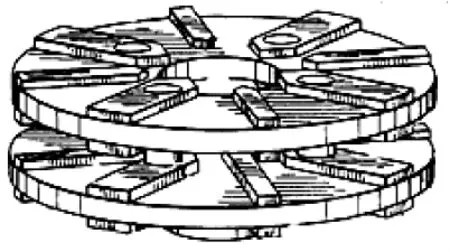
图2 高扬程圆盘泵叶轮结构

目前，国内对圆盘泵的研究较少，资料也少，大多数产品开发是采用样机开发—试验—参数修正的方法进行。随着CFD数值模拟技术的推广，通过借鉴FLUENT进行模拟试验，获取圆盘叶轮结构和性能参数，可用于指导产品开发设计，节约研发成本。

1 圆盘泵CFD模型建立

1．1 模型简化原则

1） 圆盘泵叶轮形式较多，其叶片数因为流量要求而不同。本文仅对2片圆盘间的流场进行分析。

2） 考虑到建模的可操作程度和网格的划分，将原来的圆形截面蜗壳简化为矩形截面蜗壳，即在圆盘外缘处进行流道封闭。

3） 为方便建模和网格划分，将出口段截面形状简化为矩形，此假设会影响到出口管道局部的回流现象，但不影响总体流场趋势。

4） 将泵进口段和出口段适当延长，保证了均匀的入口条件和充分发展的出口条件。

1．2 叶轮建模

由以上假设，利用Gambit软件对2个圆盘间流道进行建模，整个模型分为旋转部件和非旋转部件，其中圆盘壁面属于旋转部件，在电机带动下高速旋转，通过摩擦作用带动液体运动，壁面上凹槽是由于圆盘上存在凸脊形成的。如图3。

图3 圆盘泵计算流体模型

为节约建模时间，此处采用Gambit参数化建模的方法，首先利用AutoCAD软件建立叶片二维草图模型，输出为．Sat格式并导入Gambit中，建立一个完整的圆盘泵流体计算模型；在此基础上，运行修改此文件的．jou日志文件即可产生不同参数的圆盘泵流体计算模型。为了降低网格数量，减小计算量，采用结构化网格划分，在主叶轮区和出流段采用六面体网格，在入口段和叶轮中心区采用了四面体网格结构。如图4。

图4 计算流道网格划分

1．3 边界条件

1） 湍流模型 采用目前使用最广泛的标准k－ε双方程模型。

2） 入口边界 采用速度入口。式中，Q为体积流量；S为入口截面面积。

3） 出口边界 由于出口压力是不可预知的，同时也是流场分析需要得到的重要参数，故采用自由出口（Outflow）边界。

4） 壁面边界 圆盘壁面设为无滑移运动壁面，与圆盘流道内的设定流体区域同时旋转，其他为无滑移静止壁面。

5） 坐标系 圆盘流道内设定的特定区域的流体设为旋转坐标系，其他为静止坐标系。

6） 流场区域交界面 根据建模需要将整个流场划分了几个区域，不同区域采用的坐标系不同，为了实现区域交界面的数据交换，将交界面设为交互的Interface边界条件［7－9］。

2 单因素分析

2．1 不同外径对最大压升影响

图5a为圆盘叶轮内径相同，圆盘凸脊数量及布置形式固定，圆盘外径不同的圆盘叶轮CFD计算模型。利用FLUENT软件对图5a所示的模型进数值分析，得到图5b，流量为100m3／h，叶轮转速为2 000r／min。由图5b知，随着圆盘叶轮外径的增加，净压升呈直线递增趋势。

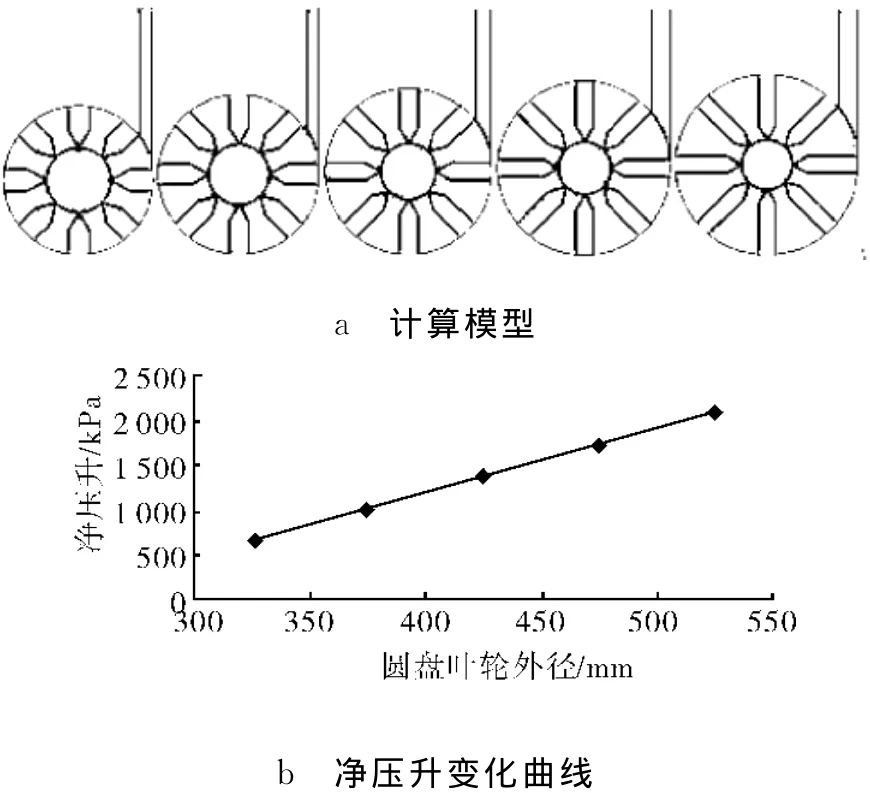
图5 不同外径圆盘泵计算模型和净压升变化曲线

2．2 不同内径对最大压升影响

图6a为圆盘叶轮外径固定，自左向右内径逐渐增大的CFD模型示意图，从图中可以看到此时的出口段截面形状和长度保持一致，由于内径的差异使的入口段存在较大差异，但由于对入口段做了延伸处理，保证了模拟分析有一个充分稳定的入口条件。

图6b为流量为100m3／h，叶轮转速为2 000 r／min，圆盘外径一定，圆盘泵净压升随圆盘内径变化曲线。从图中可以看出，随着内径的增大，净压升值逐渐降低的变化趋势。

图6 不同内径圆盘泵计算模型和净压升变化曲线

2．3 不同圆盘间距对最大压升影响

不同圆盘间距下，圆盘泵净压升随圆盘间距变化曲线如图7所示。由图7可知，随着圆盘叶轮间距的增大，净压升先增大后减小，最大净压升并没有出现在圆盘间距最小的情况下，其最大压升出现在某一值后，随着圆盘间距的增大，其最大压升逐渐减小。

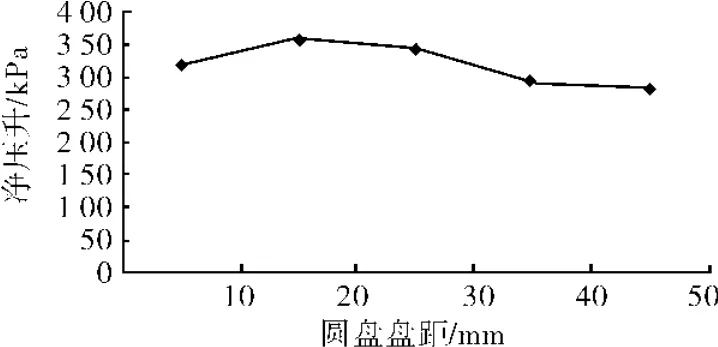
图7 不同圆盘间距下圆盘泵净压升变化曲线

图8所示为不同凸脊（叶轮）高度下圆盘泵净压升比变化曲线。由图8可以看出，在某一圆盘间距下，随着凸脊高度所占圆盘间距比例的增大，圆盘泵净压升比重增加；在15%～30%的比例情况下，其净压升值变化不大。

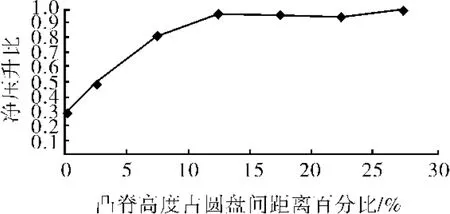
图8 不同凸脊（叶轮）高度下圆盘泵净压升比变化曲线

3 正交试验分析

3．1 正交试验表设计

正交设计是多因素的优化设计方法，也称为正交试验设计。其过程是在全部试验样本中挑选出部分代表性的样本点进行试验，且这些点具有正交性，正交表利用正交性原理编制并已标准化，科学安排试验方案并对试验结果进行计算分析［10－11］。

本文以获取圆盘泵最大压升为目标进行正交试验设计分析。从目前掌握的圆盘泵相关研究资料分析可得，影响压升的因素包括圆盘外径、圆盘间距、圆盘内径，流量、流体粘度密度特性等。由于圆盘泵性能受流体特性影响较明显，为使试验结果具有可比性和提高试验精度，降低试验干扰因素影响，按照均衡分布的思想，对不同粘度和密度组合进行区组设计。同时在圆盘外径因素中采用拟水平法，用标准正交表来安排试验。在此仅考虑5个因素，设计正交试验L16（45）并进行编码，如表1所示。

表1 因素水平

3．2 试验结果分析

为评价上述5种不同因素对圆盘泵扬程的影响，寻找影响圆盘泵扬程的主次因素及其优化方案，此处针对其正交试验结果进行了极差分析，分析结果如表2所示。由表2极差分析可知：对压升影响最主要的因素是圆盘外径，其下依次为圆盘内径、圆盘间距、流量，由此确定最佳参数组合为A3B3C1D1。也就是说流体在圆盘叶轮流道内经圆盘过流区域越大，流量较小，圆盘间距越小的情况下，可以获得更大压升值。

表2 试验方案与结果分析

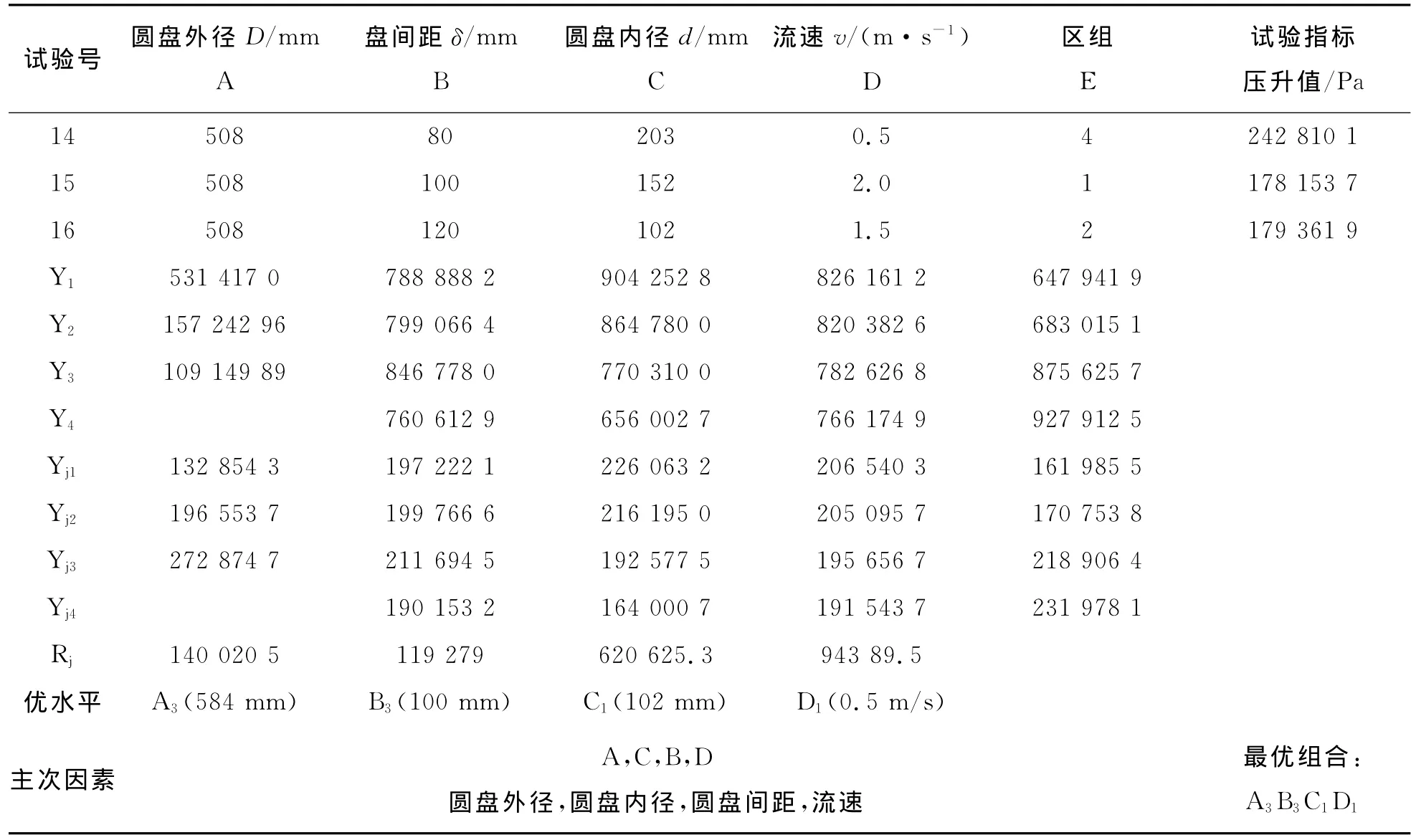
续表2

4 结论

1） 通过对圆盘泵叶轮流道进行合理的简化后，利用Gambit建立参数化模型，并进行网格划分，给出湍流模型、边界条件以及求解策略，为类似结构的CFD分析提供了有效的方法。

2） 利用FLUENT软件分别针对影响圆盘泵最大压升的参数进行单因素分析。在相同参数下，圆盘泵净压升随叶轮外径的增大而增大，随圆盘叶轮内径的增大而减小；在圆盘叶轮其他参数不变的情况下，圆盘泵净压升随圆盘间距的增大，其最大压升先升高后降低；在圆盘叶轮其他参数不变的情况下，圆盘泵净压升随圆盘凸脊高度的增大而增大，但当凸脊高度大于圆盘间距的15%以后，净压升不再随凸脊高度的变化而变化。

3） 以获得最大压升为试验优化目标，综合拟水平法和区组试验原则，利用正交试验的原理，制定正交试验表，对16种结构进行仿真计算，通过方差分析确定圆盘叶轮结构参数规律，为圆盘泵结构的设计和产品开发提供参考依据。

［1］ Max I Gurth．Rotary Disc Pump：United States Patent， 4940385［P］．1990－07－10．

［2］ Max I Gurth．Method and apparatus for pumping large solid articles：United States Patent，4335994［P］．1982－06－22．

［3］ Max I Gurth．Method and apparatus for pumping fragile articles：United States Patent，4514139［P］．1985－04－30．

［4］ Max I Gurth．Method for pumping fragile or other article in a liquid medium：United StatesPatent，4768920［P］．1988－09－06．

［5］ Max I Gurth．Rotary disc slurry pump：United States Patent，4773819［P］．1988－09－27．

［6］ Max I Gurth．Rotary Disc Pump：United States Patent，7097416B2［P］．2006－08－29．

［7］ 周昌静，陈国明，高本金，等．海底泥浆举升叶片圆盘泵轴向力预测［J］．石油矿场机械，2011，40（3）：28－31．

［8］ 周昌静，陈国明，徐长航．叶片圆盘泵固液两相流动规律数值模拟［J］．中国石油大学学报：自然科学版，2010，34（5）：147－151．

［9］ 黄志凌，冯勇建．不同形状叶轮对潜油离心泵内数值流场的影响［J］．石油矿场机械，2011，40（3）：36－39．

［10］ 韩占忠，王 敬，王小平．Fluent流体工程仿真实例与应用［M］．北京：北京理工大学出版社，2004．

［11］ 栾 军．现代试验设计优化方法［M］．上海：上海交通大学出版社，1995．

Optimization on Structural Parameter of Disc Pump Impeller Based on Orthogonal Digital Simulation

WANG Shao－ping1，GAO Ben－jin2，YIN Shu－meng2，ZHOU Chang－jing2
（1．Oilfield Construction Corporation，CNOOC Base Group，Tianjin300000，China；2．Centre for Offshore Engineering and Safety Technology，China University of Petroleum，Qingdao 266580，China）

According to the impeller structure characteristics of the disc pump，the CFD models，which realized the parametric modeling on parts of structure and operation parameters，were established，by using the FLUENT software．Aiming at obtaining the biggest pressurizing，the single factor or multi－factors were analyzed separately，and a 5factors 4levels orthogonal experiment table was formulated，and CFD analysis was applied on 16kinds of structure separately，in consequence．On the basis of the orthogonal experiment results，an optimum structure was proposed and the primary and secondary factor orders，which may affect the maximum pump head，were obtained．This may provide the reference for the designation of the disc pump．

disc pump；FLUENT；orthogonal design method；numerical simulation

book=36,ebook=36

TE952

：A

1001－3482（2012）06－0058－05

2012－02－10

国家科技重大专项课题“深水油气田开发钻完井工程配套技术”（2008ZX05026－001－12）

王少平（1960－），男，海南人，高级工程师，1982年毕业于华南理工大学，主要从事海洋石油工程领域的技术工作，E－mail：wangshp3＠cnooc．com．cn。