基于标准层及改进遗传算法的剩余油测井评价

王婧慈，郭海敏

（1.长江大学油气资源与勘探技术教育部重点实验室，湖北 荆州 434023；2.长江大学地球物理与石油资源学院，湖北 荆州 434023）

0 引 言

中子寿命测井的主要目的是确定剩余油饱和度及其纵、横向分布，但此类过套管脉冲中子饱和度测井的影响因素较多[1－2]。在实际测井解释工作中，针对具体研究区块或关键油组，较难将多个因素剥离进行实验研究，且各影响因素的地区差异性较明显，导致前人的研究成果较难推广。为将各影响因素综合考虑并提高测井解释精度和效率，本文探讨了一种可以涵盖多重影响因素的快捷测井解释方法，该方案将各井次、各油组测井资料的二次校正和解释模型参数估计融合考虑，利用轮南地区实际资料对比验证了可行性。

1 设计遗传算法参数及测井数据处理流程

遗传算法在地球物理学中应用广泛[3－5]。有文献证明经典遗传算法在实际应用中易出现一定问题，也提出了一些解决方案[6－9]。自适应遗传算法[10]在交叉和变异概率的调整上引入了自适应机制，但经典的自适应遗传算法参数调整机制较简单，解决具体问题时有待改进。

设计思路。① 初期群体多样性较强时，减小高、低适应度个体选择概率的差距，适当增大交叉概率；当算法收敛较稳定时，扩大高、低适应度个体选择概率的差距，适当减小交叉概率，这样有助于在初期增强算法搜索能力，防止早熟现象，在算法趋于收敛时防止优良基因被破坏；② 适应度较小的个体对应较大的交叉、变异概率；反之亦然。

1.1 选择概率设定

将某个体被选中的概率与其适应度函数建立关系式

式中，F为该个体的适应度。若将归一化处理后的P写作p′、F写作f，当F取值范围为[1，∞）时，有p′≥f。在算法运行初期将p′用作选择概率可加大适应度较小个体被选择的概率，防止算法过快收敛于局部最优解。将该代群体平均适应度表示为¯F。令≤A时，选择概率为p′；＞A时，选择概率为f。其中A为可变参数，根据适应度期望值确定。本文中子寿命测井孔隙度建模中A＝1.5；含水饱和度建模中A＝2.5。

1.2 交叉概率pc设定

当F≥¯F时

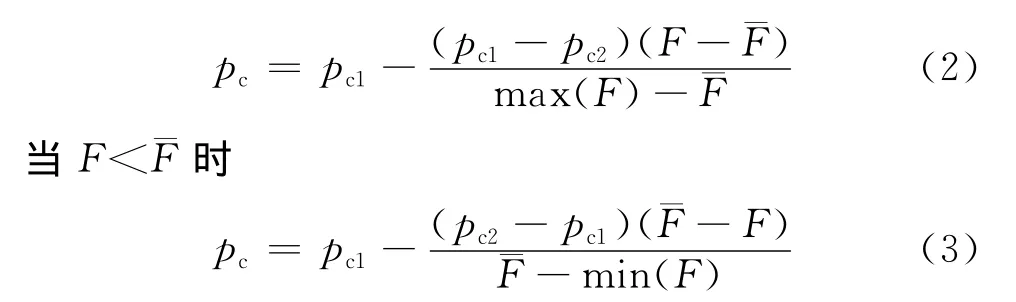
式中，pc1为适应度值恰好等于¯F的个体所对应的交叉概率，取值范围（pc2，0.5）；pc2为适应度值最大的个体所对应的交叉概率，取值范围（0，pc1）；max（F）、min（F）分别为该代群体中最大、最小适应度。

1.3 变异概率pm设定

式中，pm1为适应度值等于¯F的个体所对应的变异概率，取值范围（pm2，0.1]；pm2为适应度值最大的个体所对应的变异概率，取值范围[0.0001，pm1）。这里pm1为0.09，pm2为0.001。

1.4 算法应用流程

步骤1：设置种群规模为30。若测井解释模型中有N个未知参数，根据各参数进化范围和所要求的精度进行二进制编码。

步骤2：解码。若参与运算的样本点数目为n，将个体i代入待确定参数的模型中，计算出真实值与计算值之间的误差

令

为保证适应度取值范围为[1，∞），令适应度

步骤3：选出该代适应度最大的个体与当前存储的最优个体比较，将适应度较高的个体作为当代最优个体存储起来，并保留该个体直接进入下一代。

步骤4：判断是否满足算法停止准则。若满足则停止，否则，产生下一代。回到步骤2。

1.5 算法停止准则的设定

2 改进算法在中子寿命测井解释中的应用

将经过常规预处理的测井资料利用本文方法进行二次处理可确定解释参数，相当于进行了二次校正。

2.1 标准层的选取

开采层段或注入水波及层段的物性特征与完井相比可能已经发生了一些变化。本文采用标准层研究方法，在单井处理时，首先结合地质和生产资料，针对每个油组选择合适的标准层。

标准层必须满足条件：①区域上沉积稳定，并具有一定厚度；②必须是未经开采及注入水未波及的相对封闭段；③与待评价油组的垂向距离在一定范围内，岩性物性与待评价油组较一致；④至少有几口关键井在标准层有取心资料；⑤历年中子寿命测井和裸眼井测井曲线的对比能够验证标准层的稳定性，如完井自然伽马与新测得的自然伽马曲线相符度较高，历年中子寿命测井曲线形态较一致。图1为轮南地区侏罗系油组标准层在LN2-×-×A井的测井曲线实例。

图1 LN2-×-×A井标准层实例

2.2 孔隙度模型结构的建立及参数确定方法

地层孔隙度与热中子近、远探测器计数率比值具有一定关系[11]。本文选用轮南油田2井区侏罗系（J）、三叠系（T）标准层岩心孔隙度资料，分别建立中子寿命测井近、远计数率比值与孔隙度关系模型的结构（见图2、图3），以下称之为中子寿命测井孔隙度模型结构。其一般表达式为

图2 侏罗系中子寿命测井孔隙度模型

图3 三叠系中子寿命测井孔隙度模型

式中，R为近、远计数率比值；A、B、C为待定系数。

孔隙度较大时，地层水矿化度对近、远计数率比值与孔隙度的关系有一定影响[11]，因此有必要针对每个井次、每个油组讨论中子寿命测井孔隙度模型参数。若某井次标准层中可选用的样品点数目为n，将孔隙度模型、R值以及岩心资料（若无岩心资料可用精度较高的完井解释结论代替）利用1.4节中所述流程处理，此时真实值Aj为样品点完井孔隙度，迭代所得最优解为适应于该井次、该油组的孔隙度模型参数。

2.3 含水饱和度模型及参数确定方法

中子寿命测井含水饱和度模型表示为[12]

式中，Sw为含水饱和度，小数；Σ为测得的地层热中子宏观俘获截面，c.u.；φ为地层孔隙度，小数；Σma、Σw、Σh分别为混合岩石骨架、地层水、油气的热中子宏观俘获截面，c.u.；Vsh为地层泥质含量，小数；Σsh为泥质的宏观俘获截面值，c.u.。

Σma很难利用某种矿物的理论值确定；Σw在时间推移上、平面上、垂向上也具有一定非均质性。因此，有必要按照井次、油组分别确定各宏观俘获截面参数。单井解释时，若样品点数目为n，将式（10）模型和各样品点资料利用1.4节所述流程处理，此时真实值Aj为样品点完井含水饱和度，φ、Vsh利用完井测井资料，迭代所得最优解为适应于该井次、该油组的Σma、Σw、Σh、Σsh值。

2.4 中子寿命测井资料评价流程

将1.4节中的算法编入解释程序后，每个井次主要解释流程见图4。

图4 中子寿命测井解释流程图

3 评价效果对比举例

3.1 自适应遗传算法改进效果示例

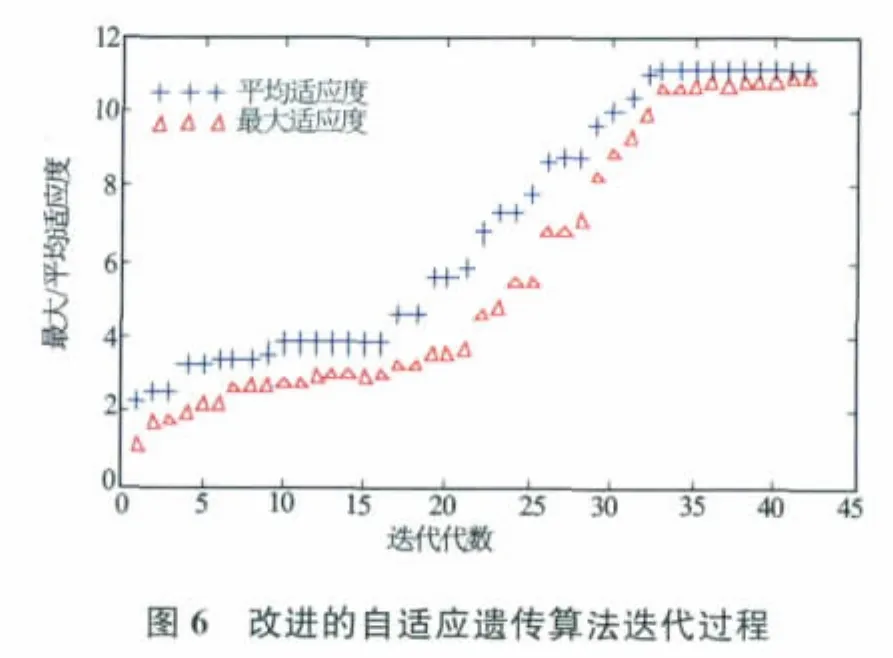
根据实验分析及宏观俘获截面理论值[1]确定各待定解释参数的进化范围（见表1）。为验证算法的优越性，利用常规算法和本文算法分别处理关键井次（见表2）。图5、图6为LN2-×-A 井三叠系油组饱和度模型参数求取过程，可见改进的算法收敛平稳，速度更快。

表1 各模型参数进化范围

3.2 剩余油评价效果验证

图7为LN2-×-×D井侏罗系4597～4617m层段2004年、2005年、2006年中子寿命测井评价图。该井2005年1月对侏罗系JⅣ油组4609～4615m层段射孔，投产日期为2005年3月7日。中子寿命测井日期分别为2004年12月10日、2005年12月13日、2006年2月20日，2006年单层开采产水率90%。

图7中可见从原测井解释结果中较难得出结论，而新测井解释结果与裸眼井资料、实际生产情况相符度较高。轮南2井区水淹层孔隙度较完井孔隙度普遍稍有降低。根据新的测井解释结果，2006年4611.5～4615m段判断为高水淹层，但4609～4611.5m段判断为低水淹层。这一结论也可从其他测井资料得到支持，如4609～4615m见2005年、2006年自然伽马异常，水淹特征明显。但从完井渗透率、自然电位等可见4611.5～4615m段较4609～4611.5m段渗透性更好，水淹程度差距较大是合理的。

将本文讨论的方法应用在轮南油田2井区多个井次的中子寿命测井评价中，通过与实际生产数据对比（见表3），可见中子寿命测井解释结果与生产结论相符程度较高。

表2 常规算法与改进算法性能对比

表3 中子寿命测井解释结果与实际生产情况统计

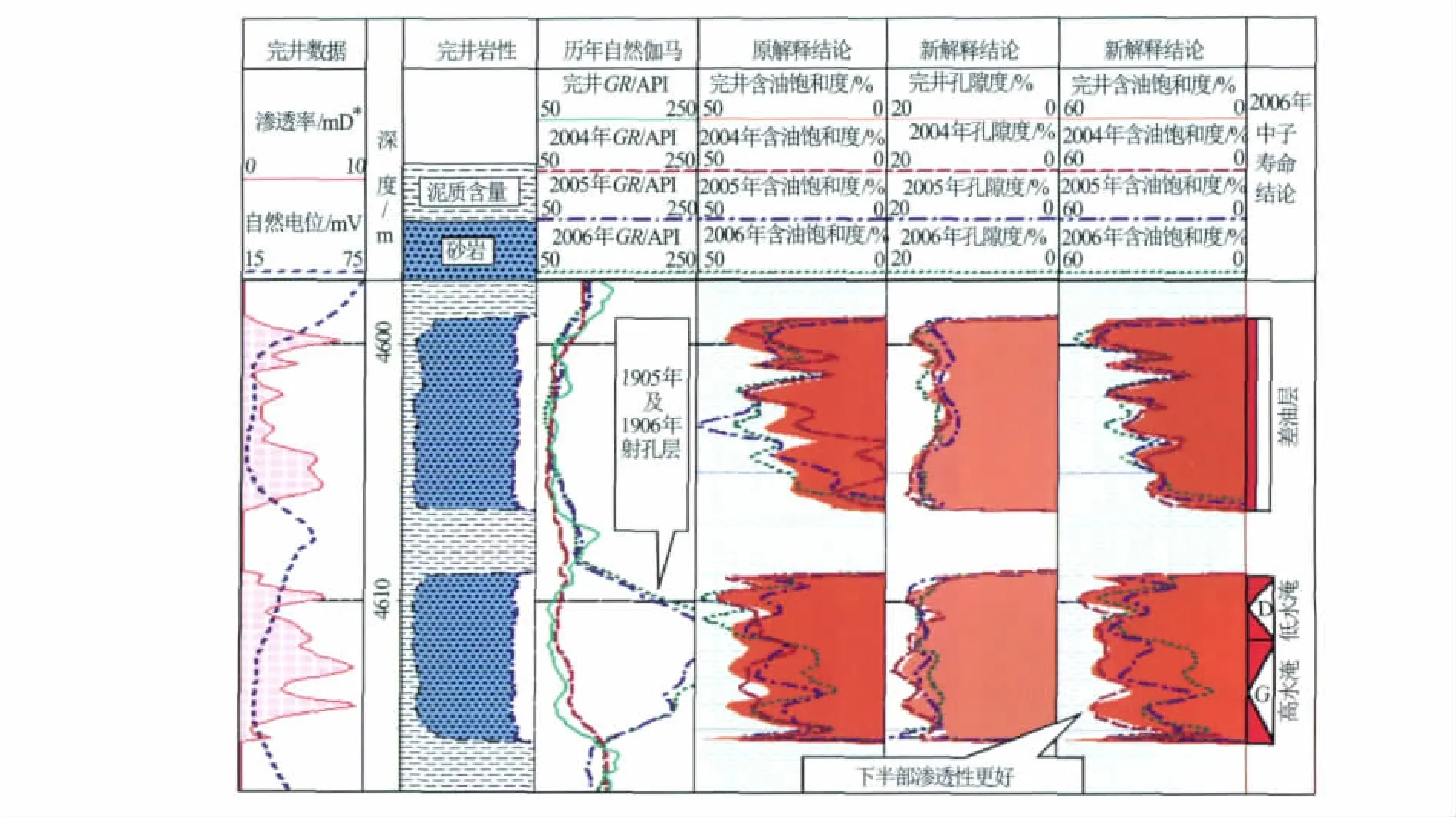
图7 LN2-×-×D井中子寿命测井资料评价结论

4 结 论

（1）油藏开发中选定相对稳定的标准层作为参照，分析每个井次在标准层上的特征，相当于将各井次、各油组放在统一标准下研究，为测井解释精度的提高奠定了基础。

（2）对自适应遗传算法的改进有效地提高了算法的效率。将算法编入测井解释程序后获得了更有针对性的解释参数，为解释参数的确定提供了一条便捷可行的途径。

（3）将改进的自适应遗传算法和标准层测井解释法相结合可为孔隙度的再评价、剩余油饱和度的计算提供有力保障，若再结合产水率、驱油效率等结论，可为油藏动态监测提供帮助。

[1]肖培琛，李耀文，万舒.放射性测井基础与中子寿命测井[M].北京：石油工业出版社，2007，73-115.

[2]刘文辉，章成广，杨天荣，等.中子寿命求剩余油饱和度影响因素探讨[J].工程地球物理学报，2008，5（6）：692－695.

[3]陈钢花，董维武.遗传神经网络在煤质测井评价中的应用[J].测井技术，2011，35（2）：171－175.

[4]Mogbolu P O，AKINOL O.Application of Genetic Algorithm in Deconvolution of Logs[C]∥SPE 150743，Nigeria Annual International Conference and Exhibi－tion，30July－3August 2011，Abuja，Nigeria.

[5]谭锋奇，李洪奇，孟照旭.数据挖掘方法在石油勘探开发中的应用研究[J].石油地球物理勘探，2010，45（1）：85－91.

[6]Vasconcelos J A，Ramrez J A，Takahashi R H C，Saidanha R R.Improvements in Genetic Algorithms[C]∥IEEE Transactions on Magnetics，2001，37（5）：3414－3417.

[7]Kuo T，HWANG S Y.A Genetic Algorithm with Disruptive Selection [C]∥IEEE Trans.on Systems，Man，and Cybernetics——Part B：Cybernetics，1996，26（2）：299307.

[8]于志刚，宋申民，段广仁.遗传算法的机理与收敛性研究[J].控制与决策，2005，2（9）：971－980.

[9]Rudolph G.Convergence Analysis of Canonical Genetic Algorithms[J].IEEE Trans on Neural Networks，1994，5（1）：96－101.

[10]Srinvivas M，PATNIK L M.Adaptive Probabilities of Crossover And Mutation In Genetic Algorithms[C]∥IEEE Transactions on Systems，Man and Cybernetics，1994，24（4）：656－667.

[11]张锋，徐建平，胡玲妹，等.PNN测井方法的蒙特卡罗模拟结果研究[J].地球物理学报，2007，50（6）：1924－1930.

[12]郭海敏.生产测井导论 [M].北京：石油工业出版社，2010：478－499.