EM-MWD信号沿钻杆传输模型有限元分析

刘庆龙，冯纪成

（1.中国石化胜利油田钻井工艺研究院钻井测量仪器研究所，山东 东营 257017；2.中国石化胜利油田钻井工艺研究院随钻测控技术研究所，山东 东营 257017；3.中国石化华东石油管理局钻井工程公司，江苏 镇江 212003）

0 引 言

近年来，自动化钻井对井内数据的大量需求促进了井下与地面实时通信技术的发展，其中EMMWD技术得到了广泛研究和应用。由于磁场信号在地层中衰减迅速，EM-MWD系统主要依靠电感应场实现信号传输[1－2]，其基本工作原理是由井底电流源激发电磁信号，经由地层传输后，在地面通过检测2个插地电极之间的电势差完成信号接收，其传输性能主要受到载波频率、地层参数、传输信道、地面检测方式、发射天线结构等方面影响。

为掌握EM-MWD信号在地层中传播都受哪些因素的制约及其制约程度，从20世纪70年代开始，研究者们已经基于不同理论和分析方法提出了各种信道／传输线模型。其中具有代表性的有James R Wait和David A Hill[3]1979年提出的与钻杆同轴的环形线圈的磁激励分析模型，并且利用数值模拟分析方法计算了电流在钻杆上的分布规律；J M Carcione和F Poletto[4]根据切比雪夫展开式和傅里叶频域分析方法，提出的低频电场信号沿钻杆传播的时域算法模型以及熊皓和胡斌杰[5－6]提出的非对称偶极子分析模型。

本文改进了非对称偶极子的分析方法，提出有限元分析模型，将钻杆作为接收天线并检测其上的电流分布，再计算出地下电场或电压分布情况。

1 传输信道模型及其对比验证

该模型采用直接激励方式（见图1），传输模型原理示意图如图2所示。l1为钻杆上半部分的长度，lgap为中间绝缘段的长度，le为下部钻杆（电极）的长度，a为钻杆外半径。

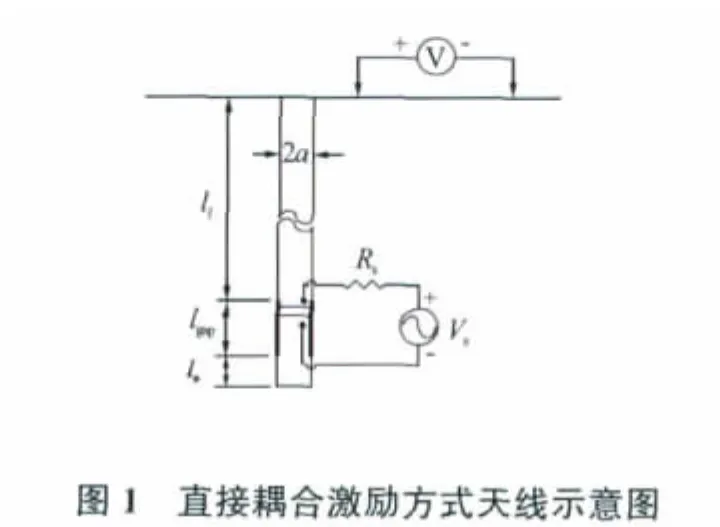
假设，① 钻杆和钻井液的影响可忽略；②地层为电阻率在2.5～20Ω·m之间。设在y＝0平面地下某点（x，z）的电场检测值为，它由点（x′，z′）处电流元激发，则该点电场强度可以表示为

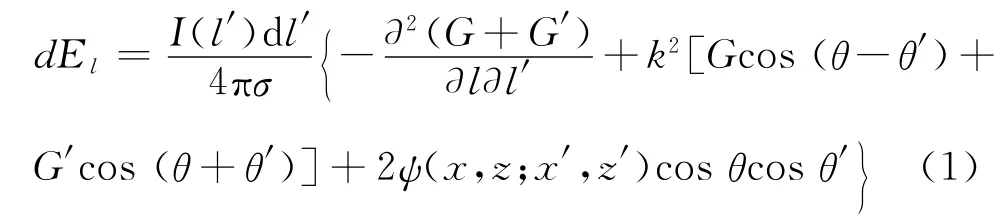
式中，k2≈iωμ0σ；σ为地层电导率；e－iωt为时间因子。

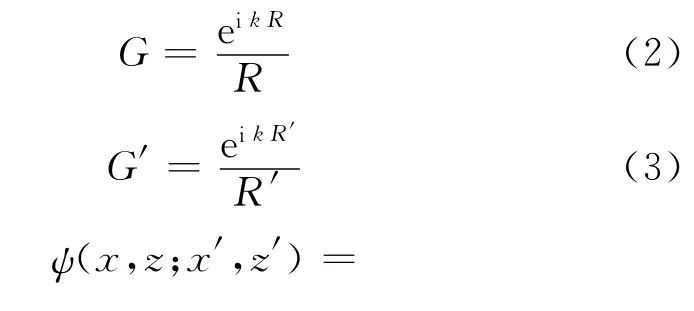
当｜p｜≤q≤｜kR′｜≤1时，由Bessel-Hankel公式可得ψ≈0。

假设I（l′）是钻杆上分布的电流，并且满足I（0）＝I（L）＝0，对式（1）从0到L积分就可以得到全部的电流分布公式

对式（6）可以用 MoM 法求出I（l′）。然后将钻杆分成 N 份，每份的中点坐标为（x′n，z′n），单位长度为Δl′n，角度为θ′n。另每个电流元两端的电流值为I（n－1）和I（n），得到

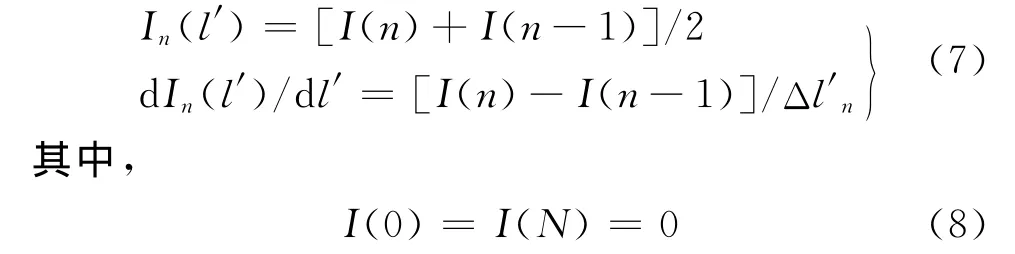
将式（8）代入式（5）然后对整理成长度的数列，得到

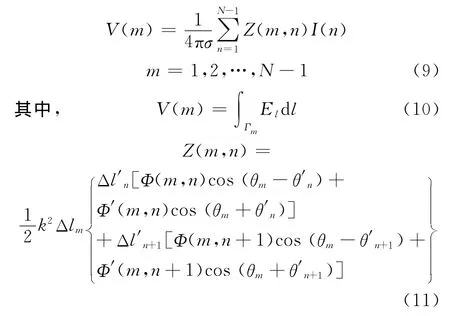
最后分别得到电场和上部钻杆与接收电极间的函数

为简化计算，井下激励为10W，地面检测距离为50m，地层电阻率分别为20Ω·m和25Ω·m，采用以下参数进行仿真并与文献[5]和文献[6]的传输模型进行对比验证（见图3、图4，文献所用模型用实线表示，本文方法用点表示）。

对比发现，①相同发射频率时，地面接收电压随着深度的增加而降低；②相同地面接收强度时，传输深度随频率的增加而减小；③相同传输深度时，地面接收电压的强度随频率的升高而降低；④上述情况随着地层电阻率的增加而增加，而且2个模型具有很好的一致性，说明该模型有效。

2 信道传输的影响因素分析

2.1 地层及钻井液电阻率的影响

由图3和图4可知在其他条件一定情况下，电阻率越低，电磁信号衰减越严重，地面接收到的有效信号也越微弱。

由于模型中没有考虑钻杆内阻和接头阻抗，在盐水中进行金属棒的垂直电流分布测试。图5（a）是未考虑表面阻抗影响的结果，图5（b）是对表面阻抗进行小幅调整之后的结果。图5中的点为实测值，线为理论计算值，通过对比可见，当钻杆在类似盐水这种低电阻率的介质中应用时，钻杆的表面阻抗的影响将不能忽略。

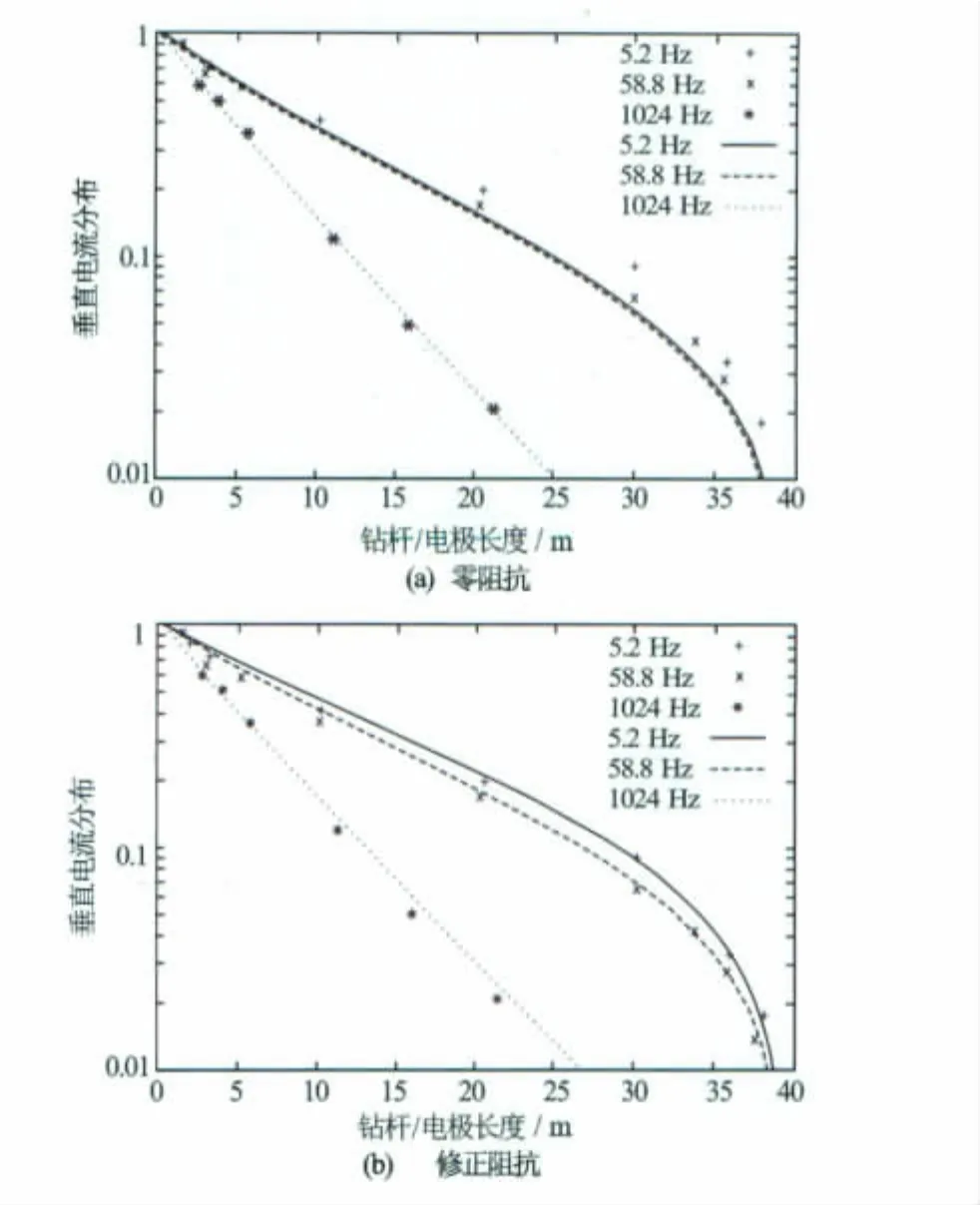
图5 表面阻抗与电流关系

2.2 钻杆因素的影响

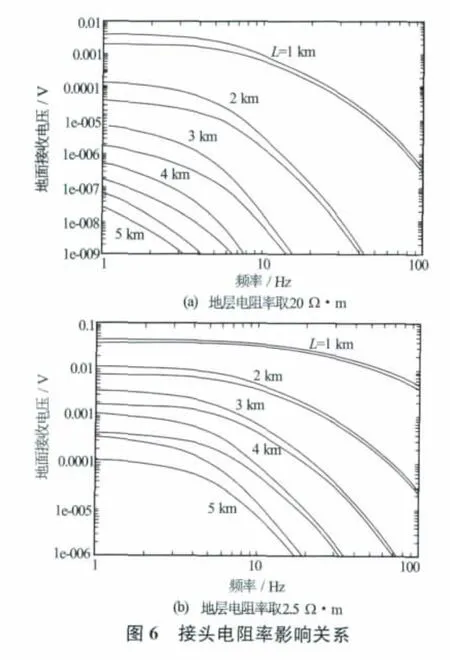
其他参数同上，钻杆电阻率取2×10－7Ω·m，磁导率取100，仿真结果见图6，实线表示钻杆电阻率为0，虚线表示钻杆电阻率为0.25Ω·m。图6（a）中地层电阻率取20Ω·m，图6（b）中地层电阻率取2.5Ω·m。可见钻杆电阻率的影响比较明显，为提高模型精度就必须考虑钻杆电阻率。

2.3 载波频率的影响

从图3和图4可知频率越低衰减越小，传输距离也就越远。但是并不是频率越低越好，必须依据应用的实际地层参数和数据传输率共同决定。以图4为例，根据仪器所能检查的最大精度为界，如图7中横线所示。

所用仪器的最大信噪比、实际地层情况以及设计孔深决定了载波的最大频率，但是最小频率要由所需要的信号传输速率而定，必须保证最大载波频率满足最小数据传输速率，否则就不能应用遥测式EM-MWD设备。

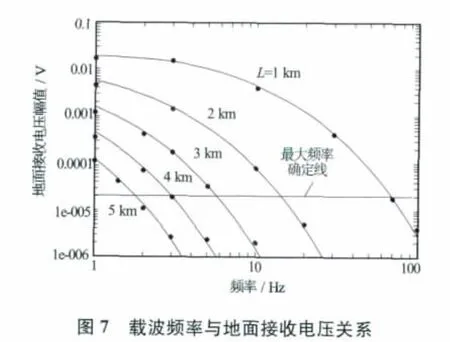
需要说明的是图4是地层电阻率比较低的情况，图3是地层电阻率比较高的情况，对比发现，其实当频率低于一定数值后，降低频率对地面检测电压的贡献已趋于常值，也就是对于有效传输深度而言并不能增加多少。

2.4 地面检测距离的影响

图8是地面检测距离与电场强度的仿真结果。从图8中可见，相同频率下距离信号源水平距离越远，感应电场强度越低，但是当水平距离达到一定值（约为50m）后，这种变化趋于一个常数。所以地面检测的水平距离一般取50m处为佳，过近或过远都不宜，尤其是过近会使检测信号受到地面设备干扰严重，不利于提高信噪比。

图8 水平检测距离与电场强度关系

3 结 论

（1）提出了一种基于有限元方法的EM-MWD信道分析模型，并总结了影响信号检测的几种因素及其影响规律，指出钻井液和钻杆的电阻率在传输过程中的影响比较明显，不能忽略。

（2）载波频率应当根据实际地质条件和设备情况综合考虑。

（3）地面检测两极之间的距离不宜过远。

（4）该方法不足之处在于分析模型过于简化，诸如地层各向异性和钻杆接触阻抗以及地面环境、噪声源等没有进行详细分析和讨论，有待进一步的深入研究和完善分析模型。

[1]James R Wait，David A Hill.Electromagnetic Basis of Drill-rod Telemetry[J].Electron，1978，14（17）：532-533.

[2]Ivo Steiner.Electromagnetic MWD／LWD－Where and Why[J].Rudarsko－geoldko－naftni zbornik，1996，8：123－128.

[3]Wait J R，Hill D A.Theory of Transmission of Electromagnetic Waves along a Drill Rod in Conducting Rock[C]∥IEEE Trans on Geosciences Electronics，1979，17（4）：21－24.

[4]Jose M Carcione，Flavio Poletto.Electric Drill－string Telemetry[J].Journal of Computational Physics，2003，186（2）：596－609.

[5]熊皓，胡斌杰.随钻测量电磁传输信道研究[J].地球物理学报，1997，5（17）：431－441.

[6]熊皓，胡斌杰.随钻测量电磁信道分析的等效传输线法[J].电波科学学报，1995，10（3）：8－14.