基于量子粒子群优化的数字冲击滤波器自动设计

余 静 吴乐南 靳 一

(东南大学信息科学与工程学院，南京 210096)

基于量子粒子群优化的数字冲击滤波器自动设计

余 静 吴乐南 靳 一

(东南大学信息科学与工程学院，南京 210096)

为了提高数字冲击滤波器设计的效率，提出了一种基于QPSO算法的优化设计方法.首先根据EBPSK通信系统中数字冲击滤波器的特殊滤波机理，在考虑有限字长效应的情况下对数字冲击滤波器进行建模，然后设计出合理的优化变量、目标函数和约束条件，并利用QPSO算法的全局搜索能力和惩罚函数法的约束处理机制设计数字冲击滤波器.仿真结果表明:种群适应度值能够逐步达到收敛，从而保证了寻优结果的最优性;设计得到的滤波器幅频响应在中心频率处呈现出极窄的陷波-选频特性，并可将EBPSK调制信号的微弱相位跳变转化为明显的幅度冲击，有利于解调.与已有的手调滤波器相比，该设计方法快速可靠，可节约0.3～0.5 dB的信噪比增益.

数字冲击滤波器;QPSO算法;EBPSK信号;有限字长效应;信噪比

无限冲激响应(IIR)滤波器的设计是数字信号处理领域中的一个重要研究分支，传统的设计方法主要分为两大类［1-2］:①利用脉冲响应不变法或双线性变换法将设计出的模拟滤波器变换为满足预定要求的数字滤波器;②无需设计模拟滤波器，直接在一定的优化准则下，使设计的数字滤波器性能最佳.前者简单，但效果往往不尽如人意，特别是在缺乏最优的模拟滤波器原型时;后者虽然跳过了模拟滤波器的设计，但现有的最小P-误差法［3］、均方误差最小法［4］和复域设计法［5］等都容易陷入局部最优解，很难得到全局最优的滤波器系数.近年来，利用群体智能算法来解决复杂、高维和非线性的优化问题取得了令人满意的效果.文献［1］提出利用遗传优化算法(genetic algorithm，GA)来设计IIR数字滤波器，该滤波器具有效果好、运算量低和通用性强的优点.文献［6］利用粒子群算法来设计IIR滤波器，也取得了一定的成效.

数字冲击滤波器［7-8］是一种特殊的 IIR滤波器，具有陷波-选频特性，可将扩展的二元相移键控(EBPSK)调制信号的相位跳变转化为寄生调幅，突出了波形差异特征，在提升解调性能的同时简化了接收机结构.目前，数字冲击滤波器依赖于人工经验设计，不仅调试耗时，而且硬件实现时系数存在有限字长效应.为此，本文提出了一种基于量子粒子群优化(quantum-behaved particle swarm optimization，QPSO)算法的数字冲击滤波器自动设计方法，合理设计了优化变量、适应度函数和约束条件，在寻优过程中一并考虑了量化效应，并通过仿真验证了该方法的高效、低误码率性能.

1 EBPSK调制解调原理

1.1 EBPSK调制

EBPSK［9-10］是一种“0”和“1”调制区间不对称的高效调制方式.常用的简化调制方式可表示为

式中，f0(t)和f1(t)分别为“0”和“1”码元的调制波形;fc为载波频率;T为码元周期;τ为波形的反相时间.码元周期T内包含N个载波周期，反相时间τ内包含K个载波周期，即T=N/fc，τ=K/fc.当仿真参数取fc=465 kHz，fs=10fc，N=40，K=2，得到了如图1所示的调制波形.

1.2 基于数字冲击滤波器的解调

数字冲击滤波器可将EBPSK信号的反相转化为幅度冲击，在滤除噪声的同时突出调制信号的波形差异，有利于解调，可辅以自适应门限判决来检测，其系统函数的表达式为

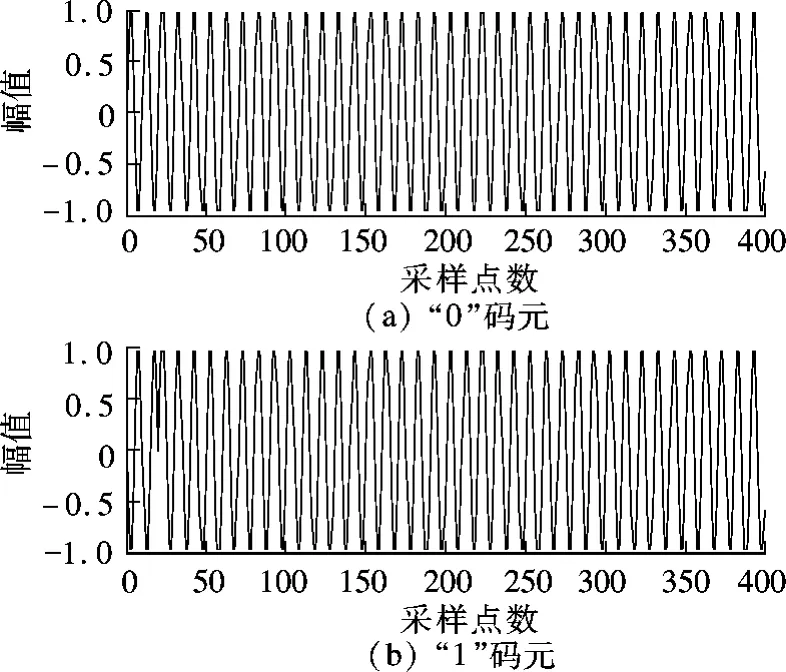
图1 EBPSK调制波形

给出一个手工调试的具有1对共轭零点和3对共轭极点的数字冲击滤波器，其幅频响应和相频响应如图2(a)所示.可以看出，在中心频率处极窄的通带内幅频响应展现出陷波-选频特性.将图1所示的“0”和“1”码元调制信号经过该数字冲击滤波器时，得到如图2(b)所示的冲击输出波形.由图可知，“0”和“1“码元的冲击输出具有明显的幅值差异.

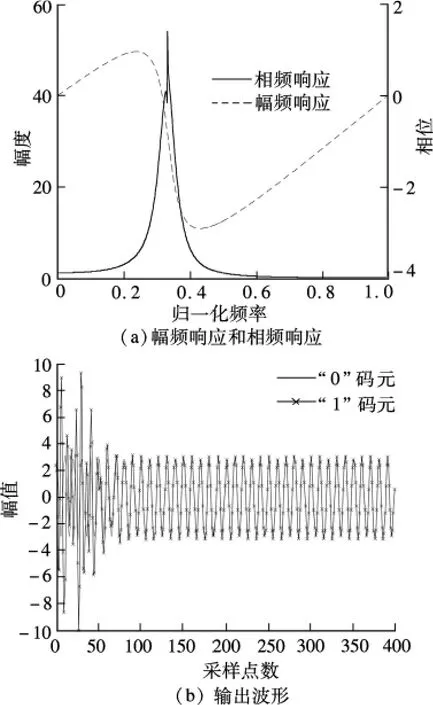
图2 数字冲击滤波器及输出波形

2 QPSO算法

基本粒子群算法［11］(particle swarm optimiza-tion，PSO)是由Kennedy和Eberhart于1995年提出的群智能算法，具有参数少、结构简单和容易实现的优点，被广泛应用于函数优化、神经网络训练和模式识别等领域.PSO算法的主要缺陷在于不能以概率1收敛于全局最优解，且收敛性能依赖于算法参数的选择［2］.文献［2］提出了一种具有量子行为的QPSO算法，同时证实了QPSO算法在保持PSO算法优点的同时具有全局收敛性.QPSO算法的整体寻优过程与PSO算法类似，只是迭代方式由简单的位移模型替代了速度-位移模型，其具体表达式为

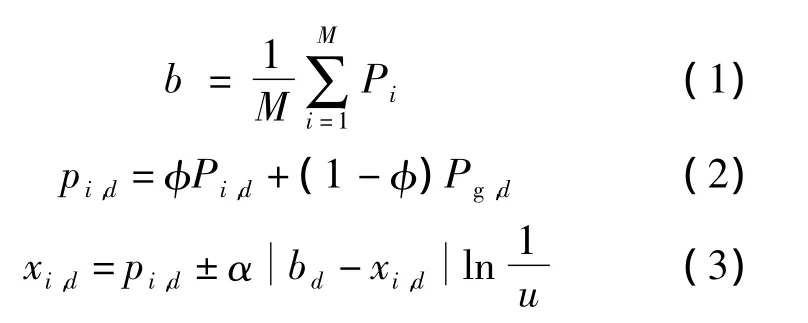
式中，b为种群平均最优位置;M为种群数目;φ和u均为分布在(0，1)中的随机数;α为压缩-扩张因子，用于控制粒子速度;pi为第i个粒子的中心吸引位置;Pi为第i个粒子位置的历史最优值;Pg为当前所有粒子位置的最优值;xi为第i个粒子的位置;d为粒子维数.

QPSO算法的具体步骤如下:

①初始化种群位置.

②根据式(1)计算种群的平均最优位置b.

③ 根据式(2)计算pi.

④根据式(3)计算粒子的新位置xi.

⑤对新位置进行边界限制后计算其适应度值，并决定是否更新个体历史最优值Pi和种群全局最优值Pg.

⑥若未达到最大历史迭代次数，转为步骤②;否则，输出全局最优并结束.

3 基于QPSO的冲击滤波器自动设计

手工调试是目前数字冲击滤波器设计的主要方法.参考文献［7］的研究结果，在手工调试中，将零极点的半径和相角限定在一定范围内，并以固定步长增长，找到一组合适的零极点使得滤波器中心频率处极窄的带宽内呈现出陷波-选频特性，使“0”和“1”码元经过滤波器后幅值差异很大.以上步骤均需要人工查看结果并反复比较，故手工调试系数效率不高，且不能保证最优.鉴于此，本文提出了一种基于QPSO算法的自动设计方法.

3.1 数字冲击滤波器模型

考虑含有1对共轭零点、3对共轭极点的数字冲击滤波器，其传递函数可表示为

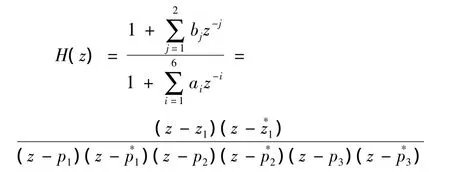
式中，z1=rzejwz，其中rz和wz分别为零点的半径和相角;pk=rkejwk，其中rk和wk为分别第k对极点的半径和相角.

3.2 量化效应

为了克服手工调试设计方法中硬件实现时系数存在有限字长效应的缺点，本文在优化过程中考虑有限字长效应，保证优化系数量化后在同等字长下解调效果依旧最优.此外，数字冲击滤波器采用稳定性较好的格型结构.具体的量化处理流程如图3所示.

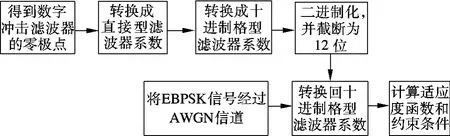
图3 量化处理流程

3.3 优化变量的确定

本文设计的数字冲击滤波器为包含1对共轭零点和3对共轭极点的IIR滤波器.根据文献［7］及手工调试经验，设定零点幅值和1对极点幅值分别为1和0.999 95，且3对极点的极角相同，故变量维数为4，依次为零点相角、剩余2对极点的幅值和相角.其中，零点相角的取值范围为［0.627 5，0.628 3］，2 对极点的幅值范围均为［0.80，0.95］，极点相角的取值范围为［0.628 32，0.630 00］，由此便可保证滤波器的稳定性及冲击滤波效果［12］.

3.4 目标函数

冲击滤波器能够作用于EBPSK调制信号解调的主要原因是将“0”和“1”码元调制波形中小的相位差异转换为大的幅度差异，两者的幅度差异越大则解调效果越好.为了使“0”码元和“1”码元的幅度差异最大，选用经过冲击滤波器后的“0”码元和“1”码元的波形幅度比作为目标函数.

3.5 约束函数

由3.3节的变量范围可知，零点相角小于极点相角，且中心频率位于零点和极点之间，这样保证了“1”码元相位跳变处经过冲击滤波器后呈现上凸状.为了保证上凸幅度，中心频率需要非常靠近极点，因此将载频设定在滤波器中心频率以左400 Hz内.此外，为了保证冲击滤波器的幅频响应在中心频率处呈现出极窄的陷波-选频特性，将冲击滤波器的3 dB带宽设定在500 Hz以内.3.6 适应度函数

数字冲击滤波器的优化是一个典型的多维含约束的优化问题.本文利用惩罚函数法将约束优化转化为无约束优化，具体的处理方法如下:

式中，ψ(x)为适应度函数;f(x)为目标函数，具体为经过冲击滤波器后“1”码元和“0”码元的幅度比的负值;m为约束条件的个数，由3.5节可知此处m=2;rj为惩罚因子;gj(x)为第j个约束条件，由式(5)可知需将2个约束条件转化为gj(x)≤0的形式.

4 仿真

下面通过仿真试验来验证设计方案的有效性.仿真参数设置如下:种群数目为20;最大迭代数目为10;QPSO算法中压缩-扩张因子α随着迭代的进行在［0，1］之间线性递减;系数截断位数为12;为保证冲击滤波器的3 dB带宽在500 Hz以内，惩罚因子r1和r2分别设定为1和100.算法的最终寻优结果为

其对应的直接型数字冲击滤波器系数为

由以上寻优结果可得数字冲击滤波器的幅频响应和QPSO算法适应度值的收敛曲线(见图4和图5).由图4可知，设计得到的滤波器的幅频响应在中心频率处呈现一个极窄的陷波-选频特性.由图5可知，该算法能够逐步达到收敛，保证了寻优结果的最优性.

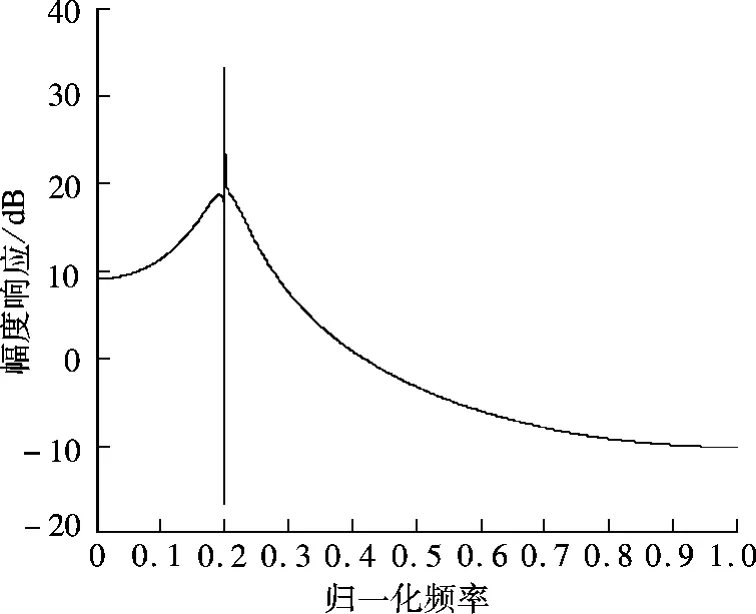
图4 冲击滤波器的幅频响应

图5 适应度收敛曲线

将EBPSK调制信号经过设计的数字冲击滤波器，可得如图6所示的冲击响应波形.由图可知，该冲击滤波器将图1中EBPSK调制信号的相位跳变转化为幅度冲击，突出了“0”码元和“1”码元的波形差异，有利于解调.图7为在系数量化为12位的情况下分别采用QPSO算法优化得到的设计系数与手工调试系数的EBPSK通信系统性能比较.由图可知，利用QPSO算法所设计的数字冲击滤波器可获得0.3～0.5 dB的信噪比增益.

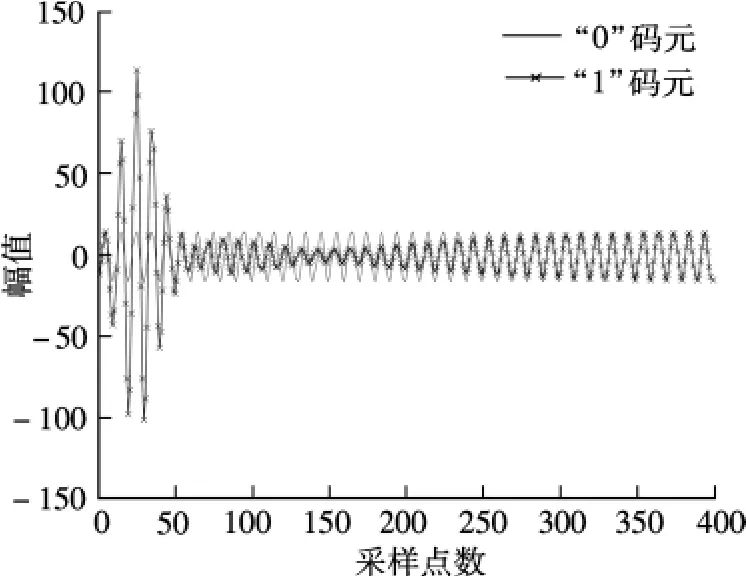
图6 冲击滤波器的输出波形对比

5 结论

本文利用QPSO算法和惩罚函数法来解决有约束函数的优化问题，提出了一种数字冲击滤波器自动优化设计方法，合理设计了优化变量、适应度函数和约束条件，且在设计过程中考虑了滤波器系数硬件实现时的字长效应，并进行了仿真验证.仿真结果表明:与传统的手工调试法相比，该设计方法快速可靠，且可以获得0.3～0.5 dB的信噪比增益.然而，本文只是初步尝试了数字冲击滤器的自动设计，最佳的自动设计方法还有待于进一步研究.

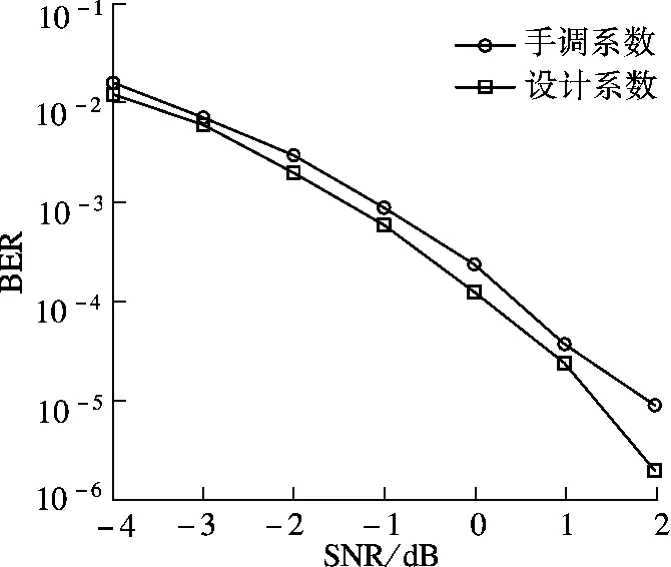
图7 误码率性能对比

［1］李建华，殷福亮.设计IIR数字滤波器的遗传优化算法［J］.通信学报，1996，17(3):1-7.

Li Jianhua，Yin Fuliang.Genetic optimization algorithm for designing IIR digital filter［J］.Journal of China Institute of Communications，1996，17(3):1-7.(in Chinese)

［2］方伟.群体智能算法及其在数字滤波器优化设计中的应用［D］.无锡:江南大学信息工程学院，2008.

［3］Deczky A G.Synthesis of recursive digital filters using the minimum P-error criterion［J］.IEEE Trans Audio Electroacoust，1972，20(4):257-263.

［4］ Shaw A K.Optimal design of digital IIR filters by modeling fitting frequency response data［J］.International Symposium on Circuits and Systems，1993，42(11):475-478.

［5］Chen X，Parks T W.Design of IIR filters in the complex domain［J］.IEEE Trans Acoustic，Speech and Signal Processing，1990，38(6):910-920.

［6］戴朝华，陈维荣，朱云芳，等.IIR数字滤波器设计的搜寻者优化算法［J］.西南交通大学学报，2009，44(6):871-876.

Dai Chaohua，Chen Weirong，Zhu Yunfang，et al.IIR digital filter design via seeker optimization algorithm［J］.Journal of Southwest Jiaotong University，2009，44(6):871-876.(in Chinese)

［7］冯熳，高鹏，吴乐南.超窄带调制信号的特殊滤波分析与仿真［J］.东南大学学报:自然科学版，2010，40(2):227-230.

Feng Man，Gao Peng，Wu Lenan.Analysis and simulation of special filtering based on ultra narrow band modulated signal［J］.Journal of Southeast University:Natural Science Edition，2010，40(2):227-230.(in Chinese)

［8］马力，冯熳，吴乐南.EBPSK数字接收滤波器设计［J］.科技创新导报，2008(28):28-29.

Ma Li，Feng Man，Wu Lenan.Design of EBPSK digital filter［J］.Science and Technology Innovation Herald，2008(28):28-29.(in Chinese)

［9］吴乐南.超窄带高速通信进展［J］.自然科学进展，2007，17(11):143-149.

Wu Lenan.Progress in ultra narrow band communication［J］.Progress in Natural Science，2007，17(11):143-149.(in Chinese)

［10］张士凯，吴乐南.EBPSK调制波的正交性及功率谱分析［J］.应用科学学报，2008，26(2):127-131.

Zhang Shikai，Wu Lenan.PSD analysis of EBPSK modulated signals［J］.Journal of Applied Sciences，2008，26(2):127-131.(in Chinese)

［11］ Kennedy J，Eberhart R.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks.Perth，WA，Australia，1995:1942-1948.

［12］高鹏.超窄带接收机冲击滤波器研究［D］.南京:东南大学信息科学与工程学院，2010.

QPSO-based auto-design of digital impacting filters

Yu Jing Wu Lenan Jin Yi
(School of Information Science and Engineering，Southeast University，Nanjing 210096，China)

To improve the efficiency of designing digital impacting filters，a novel method based on the quantum-behaved particle swarm optimization(QPSO)algorithm is proposed.First，according to the special filtering mechanism of the digital impacting filter in the communication system of extended binary phase shift keying(EBPSK)，the model of the digital impacting filter is built considering the effect of finite word length.Then the optimization variables，the objective function and the constraint conditions are designed.The global search ability of the QPSO algorithm and the constraint mechanism of the penalty method are utilized to design the digital impacting filter.The simulation results show that the fitness value is gradually converged to make sure that the optimization results are optimal.The amplitude response of the designed filter matches the digital impacting filter's characteristic of notch-select frequency in the carrier frequency，which can transform the phase hopping of the EBPSK signal into the amplitude impact so as to be good for demodulation.Compared with the existing impacting filters by manual design，the proposed design method is fast and reliable.It can save the signal-to-noise(SNR)gain of 0.3 to 0.5 dB.

digital impacting filter;quantum-behaved particle swarm optimization(QPSO)algorithm;extended binary phase shift keying(EBPSK)signal;effect of finite word length;signal-to-noise ratio

TN911

A

1001－0505(2012)02-0224-05

10.3969/j.issn.1001 －0505.2012.02.006

2011-08-02.

余静(1988—)，女，硕士生;吴乐南(联系人)，男，博士，教授，博士生导师，wuln@seu.edu.cn.

国家自然科学基金资助项目(60872075)、国家高技术研究发展计划(863计划)资助项目(2008AA01Z227).

余静，吴乐南，靳一.基于量子粒子群优化的数字冲击滤波器自动设计［J］.东南大学学报:自然科学版，2012，42(2):224-228.［doi:10.3969/j.issn.1001 －0505.2012.02.006］