全负载场景中最优调度算法长时平均性能分析
王 浩 李知航 蒋慧琳 潘志文 尤肖虎
(东南大学移动通信国家重点实验室,南京 210096)
全负载场景中最优调度算法长时平均性能分析
王 浩 李知航 蒋慧琳 潘志文 尤肖虎
(东南大学移动通信国家重点实验室,南京 210096)
首先分析了全负载场景中轮询调度、最大速率调度、比例公平调度和速率累积分布调度这4种常用调度算法.结果显示,速率累积分布调度在保证公平的基础上可以得到最好的效率,是4种调度算法中的最优算法.然后采用概率推导法给出了该调度算法的长时平均性能分析,即以轮询调度为比较基准的多用户分集增益的理论推导.该分集增益可通过短时统计结果预测长时平均性能,且可适用于任意实际场景.计算机仿真结果验证了对于该调度算法所产生的多用户分集增益理论分析的准确性,理论分析结果与实际调度结果的误差低于0.1%.
轮询调度;最大速率调度;比例公平调度;速率累积分布调度;多用户分集增益
下一代基于包交换的无线通信网络将采用合适的机会调度方法为用户提供服务[1-3].在系统中用户都为无服务质量要求,且有无限下行业务需求的全负载场景下,较好的机会调度算法则需要同时兼顾效率及公平,即在系统总吞吐量尽可能大的同时,要保证不同位置用户得到的资源数尽可能相等.对于全负载场景中现有机会调度算法中,比例公平调度已被深入研究,该算法可在效率和公平之间得到一个较好的折中[4-5].假设所有用户经历独立同分布信道,比例公平调度在公平分配资源的同时可较好地利用信道动态变化.但在实际系统中,它会偏爱离基站较近的用户,并给这些用户分配较多资源[6-7].而基于用户自身速率特性的调度,如基于“得分”的调度[7]或基于用户自身速率累积分布的调度[8-9]就不存在这个问题.从较长的时间来看,它们可在公平分配系统资源的同时较好地利用信道的动态变化.本文首先通过计算机数值仿真,比较了轮询调度、最大速率调度、比例公平调度和基于用户自身速率累积分布调度.仿真结果显示,比例公平调度和基于用户自身速率累积分布调度都可做到一定程度上效率与公平的折中.两者相比,后者效率略低,但公平性更好.当所有用户以绝对的公平方式分配相等资源时,后者可得到最大的吞吐量,说明该方法相比较其他三者可更好地利用信道的动态变化,得到更高的效率.从这个意义上讲,基于用户自身速率累积分布调度是上述4种调度算法中的最优算法.
对于采用机会调度算法系统中的任意用户,通过短时间内的检测结果预测其长时平均性能十分重要,在该系统的算法设计中必不可少.因此,本文推导了以上4种调度算法中的最优算法,即基于用户自身速率累积分布调度算法的多用户分集增益[10].多用户分集增益是指以轮询调度为基准,每个用户由于采用了机会调度算法利用信道动态变化可以得到的吞吐量与采用轮询调度可以得到的吞吐量之比.现有的多用户分集增益研究,仅对比例公平调度在所有用户经历独立同分布瑞利衰落信道时进行了推导,而缺乏对于其他调度算法及比例公平调度在实际的非独立同分布场景中的研究.这是由于不同调度算法本身特性的差异,因此多用户分集增益是与参与调度的总用户数及所有用户信道特性相关的复杂多重积分[11].而对于基于用户自身速率累积分布的调度算法,理论分析结果显示其多用户分集增益只与参与竞争的用户数及每个用户自身经历的信道状态特性有关,且可适用于用户经历任意分布的独立信道,并不局限于同分布的信道.仿真结果验证了该多用户分集增益数学推导结果的准确性,可用于系统级的算法设计,如呼叫准入控制算法、动态负载均衡算法等.
1 全负载时常用调度算法性能比较
1.1 调度算法
1)轮询调度 该算法使得参与调度的每个用户依次得到调度机会,从用户可得资源的角度来说是最为公平的方式.
2)最大速率调度 该算法在每个调度机会上都选择瞬时速率最大的用户进行调度,从系统总吞吐量角度来说是效率最优的方式.该算法计算式为
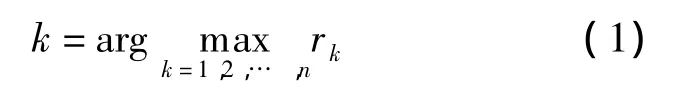
式中,rk为用户k在当前调度机会上的瞬时可得速率;n为参与调度的用户数.
3)比例公平调度 该算法在每个调度机会上选择当前瞬时速率与前一段调度机会上平均实际可得速率之比最大的用户进行调度,在一定程度上做到了效率与公平的折中.该算法计算式为
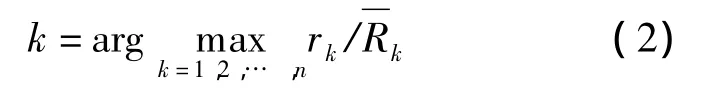
式中表示用户k在前一段调度机会上的平均

式中,Fk(rk)表示用户k对应于瞬时可得速率rk的速率累积分布函数值.
1.2 仿真比较
假设由用户反馈到基站的信道状态信息无误差且无延时,使用香农容量来进行分析,忽略由于实际的调制编码方案带来的量化误差.每次调度机会对应的调度单位大小符合LTE系统中物理资源块的定义,即频域上180 kHz,时域上为1 ms.每次仿真有10个用户参与调度,竞争10 000个调度机会,每个用户的平均信干噪比在-10~+20 dB间随机取值,参考的快衰落模型为瑞利衰落.使用所有用户总吞吐量及每用户实际得到的调度机会数来比较4种调度算法的性能,并进行1 000次仿真来得到这4种调度方法的统计性能.
图1显示了4种调度算法下,所有用户的平均总吞吐量,此处总吞吐量是指所有用户在各自被调度单位上的可得速率之和.如图1所示,采用轮询调度时,系统实际得到的总吞吐量最低,这是由于轮询调度按先后顺序依次调度每个用户,并没有利用信道快衰落带来的动态变化.而最大速率调度,由于其在每个调度机会上都选择当前可得速率最大的用户,所以该调度算法的总吞吐量最大.比例公平调度和基于用户自身速率累积分布调度,其系统总吞吐量居于最大速率调度与轮询调度之间,其中基于用户自身速率累积分布调度的总吞吐量略低于比例公平调度,这说明比例公平调度的效率略高,但代价是图2中公平性的损失较大.实际可得速率.
4)速率累积分布调度 该算法在每个调度机会上选择瞬时速率所对应的速率累积分布函数值最大的用户进行调度,最好地利用了信道的动态变化.该算法计算式为

图1 4种调度算法下用户总吞吐量

图2 4种调度算法下调度机会的累积分布
图2给出了4种调度算法下用户得到调度机会的累积分布曲线,反映了不同用户得到调度机会的公平程度.由图可见,轮询调度时所有用户得到的调度机会都为1 000,这与仿真场景设置参数一致,即所有用户都公平地得到被调度的机会,这也是该调度算法的本质,保证了用户间得到调度机会的绝对公平性.而最大速率调度,由于其一直调度有最大瞬时速率的用户,其累积分布曲线在0~10 000间分布较广,并有50%以上的用户得到的调度机会为0,其用户间得到调度机会的公平性最差.比例公平调度和基于用户自身速率累积分布调度,两者在一定程度上都较好地保证了不同位置用户得到调度机会的公平性,这2条曲线都在标准值1 000附近.从图2中的放大图中可以看到,相对于比例公平调度,基于用户自身速率累积分布调度中用户得到的调度机会更接近标准值1 000,说明其对公平性的保证更好.参考图1与图2,相对于基于用户自身速率累积分布调度,比例公平调度公平性较差,而效率略高,说明该调度算法也会偏爱平均信干噪比较高的用户,并给其分配较多的调度机会,这与文献[6-7]中的结论是一致的.也就是说,相对于前者,比例公平调度以损失公平性为代价,得到总吞吐量上的略微增益.
图3显示了当用户间绝对公平分配调度机会时,所有用户可以得到的总吞吐量.所谓绝对公平地分配调度机会,就是按各自的调度算法实际调度,当某用户得到1 000个调度机会,它就退出调度过程.图3充分说明了基于用户自身速率累积分布调度相对于其他3种调度方法的优越性.可以看到,该调度算法的总吞吐量最大,说明在保证用户间资源分配绝对公平时,该调度算法相对于其他三者,能更好地利用信道快衰落带来的动态变化,得到更好的调度效率.
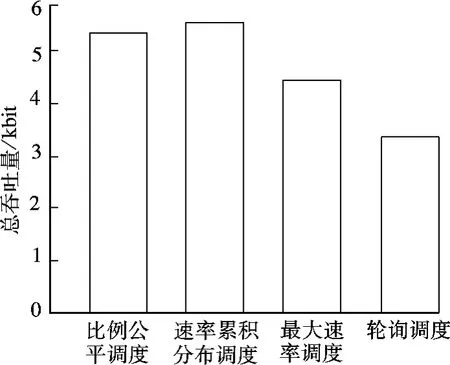
图3 绝对公平调度时4种调度算法下用户总吞吐量
基于以上仿真结果,可认为基于用户自身速率累积分布的调度算法是上述4种调度算法中的最优算法,它可以在保证用户间资源分配公平性的同时达到最大的吞吐量.而对于该调度算法,缺乏其长时平均性能的分析,而这在采用该调度算法的系统算法设计过程中是必不可少的,所以本文将对该调度算法的长时平均性能,即以轮询调度为比较基准的多用户分集增益进行理论推导.
2 速率累积分布调度的多用户分集增益
用Rk,fRk和FRk来分别表示任意用户k速率的随机变量,以及该随机变量的概率密度函数和累积分布函数.基于用户自身速率累积分布的调度,其主要思想是在每个调度机会上,选择速率累积分布函数值最大的用户进行调度,即相对于其他用户,被选用户的瞬时速率更接近于其自身由于快衰落可得的最高速率.假设Rk在一个调度单元上的瞬时值为rk,则在所有参与调度用户中,FRk*(rk*)值最大的用户k*被选择为服务用户.假设系统中共有n个服务用户,则基于用户自身速率累积分布的调度方法如式(3)所示.
众所周知,FRk(Rk)在[0,1]之间是均匀分布的[12].令 Uk=FRk(Rk),则 Uk也是[0,1]之间的均匀分布.对于用户k,当其瞬时速率为rk时,它被选中进行调度的概率为

式中,uk=FRk(rk).则用户k得到服务的概率为这表示基于用户自身速率累积分布的调度将给系统中的所有用户平均分配资源.该结论也可以由图2中每个用户得到调度机会的累积分布曲线得到验证.假设FRk(·)是一个连续单调上升函数,对于实际的物理信道,该假设是合理的.对于FRk(·)必然有唯一的反函数F-1Rk(·),则用户k在其得到服务的每个调度单元上的速率分布与F-1Rk(·)是一致的.因此,采用基于用户自身速率累积分布的调度时,用户k的长时平均吞吐量为
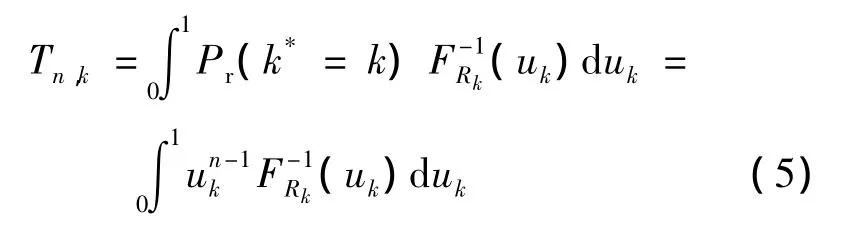
用Dn,k表示相同场景下,采用轮询调度用户k可以得到的长时平均吞吐量.则Dn,k可以看作式(5)在服务用户数n=1,可用资源数为1/n时的情况,即

定义当存在n个服务用户,并采用基于用户自身速率累积分布调度时,对于任一用户k的多用户分集增益为 Gn,k,其为 Tn,k与 Dn,k之比,即

式(7)推导的多用户分集增益适用于现实中所有的物理信道,只需统计该用户经历的快衰落信道所对应的通信速率的累积分布特性,就可以得到采用基于用户自身速率累积分布调度方法时的多用户分集增益.下面以瑞利衰落信道为例进行说明.
当用户k只考虑路径损耗和阴影衰落时的平均信干噪比λk和信道经历瑞利快衰落时,用户k的实际瞬时信干噪比t满足均值为λk的指数分布,其相应的累积分布函数为则对应于信干噪比t,在参考带宽为B时,用户k的速率Y为


其相应的累积分布函数为
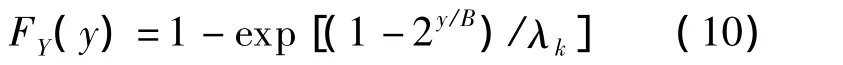
对式(10)求反函数,就可以得到多用户分集增益 Gn,k计算中所需的 F-1Rk(uk),即

在快衰落为瑞利衰落的情况下,式(7)的多用户分集增益为
由式(12)可见,当采用基于用户自身速率累积分布调度时,对其中任意用户k的多用户分集增益,只与参与调度的用户数n、用户k自身由于路径损耗和阴影衰落得到的平均信干噪比λk,及用户k本身由于所处位置与周围环境带来的信道快衰落特性有关,与调度单位的带宽及其他用户的快衰落环境无关.
3 数值仿真与结果
本节对于式(12)中推导得到的多用户分集增益Gn,k进行仿真验证.将式(12)通过数值积分计算出的结果作为理论值,将实际采用基于用户自身速率累积分布调度与轮询调度得到的吞吐量之比作为实际结果,并比较实际结果与理论分析结果的一致性,并假设最小调度单元满足3GPP LTE物理资源块的定义标准.
图4验证了某一特定用户的分集增益随总用户数的变化情况.对应于每个用户数进行了100次仿真.由图4可发现,随着用户数的增多,该用户的多用户分集增益的理论值与实际均值逐步上升.这是由于随着用户增多,每个用户有更多的机会等到其信道状态足够好时才被调度,这样被调度时其实际可得速率更接近其速率分布的峰值速率,相应的调度效率也越高,多用户分集增益也越大.从图4还可发现,该用户分集增益的理论值与实际均值两者吻合得非常好,误差低于0.1%,很好地验证了式(12)的正确性.
图5显示的是任选10个用户(用户序号1~10,对应的平均信干噪比分别为1,2,…,10 dB),每个用户的多用户分集增益的理论值与实际值的比较.可看出,实际仿真100次后平均的结果与理论值基本重合,说明式(12)对于相同数目的服务用户,由于用户所处位置不同带来的不同平均信干噪比的多用户分集增益预估的准确性.还可以发现,随着1~10号用户平均信干噪比的上升,其相应的多用户分集增益是在逐步降低的.这说明基于用户自身速率累积分布的调度方法,在保证用户间可得资源的公平性的同时,对于平均信干噪比较低也即信道条件较差的用户(如边缘用户)有较大的增益.

图4 特定用户随用户数增加时的多用户分集增益

图5 多个用户分集增益实际值与理论值比较
4 结语
首先比较了全负载场景下的4种常用调度算法(轮询调度、最大速率调度、比例公平调度和基于用户自身速率累积分布的调度),分析结果显示,基于用户自身速率累积分布的调度在保证公平性的前提下可以达到最高的效率,是以上4种调度算法中的最优算法.然后,对该调度算法的长时平均性能即其多用户分集增益进行了理论推导.该分集增益可以利用短时间内对用户信道的检测结果预测用户的长时平均性能,从而进行系统级的算法设计,且可适用于实际系统中用户经历任意分布的独立信道情况.计算机仿真结果验证了对于该调度算法多用户分集增益理论分析的准确性.
[1]Kwan R,Leung C.A survey of scheduling and interference mitigation in LTE [J].Journal of Electrical and Computer Engineering,2010,2010:273486.
[2]Li L,Pesavento M,Gershman Alex B.Downlink opportunistic scheduling with low-rate channel state feedback:error rate analysis and optimization of the feedback parameters[J].IEEE Transactions on Communications,2010,58(10):2871-2880.
[3] Oyman O.Opportunistic scheduling and spectrum reuse in relay-based cellular networks[J].IEEE Transactions on Wireless Communication,2010,9(3):1074-1085.
[4] Viswanath P,Tse D N C,Laroia R.Opportunistic beamforming using dumb antennas[J].IEEE Transactions on Information Theory,2002,48(6):1277-1294.
[5] Andrews M.Instability of the proportional fair scheduling algorithm for HDR [J].IEEE Transactions on Wireless Communication,2004,3(5):1422-1426.
[6] Wang H,Ding L,Pan Z,et al.QoS guaranteed call admission control with opportunistic scheduling[C]//IEEE Global Telecommunications Conference.Houston,USA,2011:1-5.
[7] Bonald T.A score-based opportunistic scheduler for fading radio channels[C]//Proceedings of European Wireless Conference.Barcelona,Spain,2004:283-292.
[8]Park D,Seo H,Kwon H,et al.Wireless packet scheduling based on the cumulative distribution function of user transmission rates[J].IEEE Transactions on Communications,2005,53(11):1919-1929.
[9]Patil S,de Veciana G.Measurement-based opportunistic scheduling for heterogeneous wireless systems [J].IEEE Transactions on Communications,2009,57(9):2745-2753.
[10]Soydan Y,Candan C.A feedback quantization scheme leveraging fairness and throughput for heterogeneous multi-user diversity systems[J].IEEE Transactions on Vehicular Technology,2010,59(5):2610-2614.
[11]Combes R,Altman Z,Altman E.On the use of packet scheduling in self-optimization processes:application to coverage-capacity optimization[C]//Symposium on Modeling and Optimization in Mobile,Ad Hoc,and Wireless Networks.Avignon,France,2010:98-107.
[12] Angus J E.The probability integral transform and related results[J].SIAM Review,1994,36(4):652-654.
Analysis of long-term average performance of optimal scheduling scheme in full-load scenario
Wang Hao Li Zhihang Jiang Huilin Pan Zhiwen You Xiaohu
(National Mobile Communications Research Laboratory,Southeast University,Nanjing 210096,China)
Four well-known scheduling schemes in full-load scenario,namely,round robin scheduling,max-rate scheduling,proportional fairness scheduling and cumulative rate distribution based scheduling are investigated.Results show that the last one achieves the best efficiency with a relative better fairness guarantee,which is the optimal scheme among all the four ones.Then,the probability deduction method is adopted to analyze its multi-user diversity gain,which uses round robin scheduling as the benchmark.The result can be used to predict the long-term average performance of the scheme through short-time statistical results and is applicable to all practical scenarios.The accuracy of the analysis results are verified by numerical simulations,in which the error between theory analysis and actual scheduling is less than 0.1%.
round robin scheduling;max-rate scheduling;proportional fairness scheduling;rate cumulative distributed function based scheduling;multi-user diversity gain
TN92
A
1001-0505(2012)02-0199-05
10.3969/j.issn.1001 -0505.2012.02.001
2011-10-18.
王浩(1983—),男,博士生;尤肖虎(联系人),男,博士,教授,博士生导师,xhyu@seu.edu.cn.
国家重点基础研究发展计划(973计划)资助项目(2012CB316004)、国家科技重大专项资助项目(2011ZX03003-002-02)、江苏省“六大人才”高峰资助项目、江苏省普通高校研究生科研创新计划资助项目(CXLX_0116)、东南大学移动通信国家重点实验室资助项目(2010A02,2011A02).
王浩,李知航,蒋慧琳,等.全负载场景中最优调度算法长时平均性能分析[J].东南大学学报:自然科学版,2012,42(2):199-203.[doi:10.3969/j.issn.1001 -0505.2012.02.001]

