直角域非等腰三角形凸起对SH波的散射与地震动

齐 辉，郭 晶，杨 杰

(哈尔滨工程大学 航天与建筑工程学院，哈尔滨 150001)

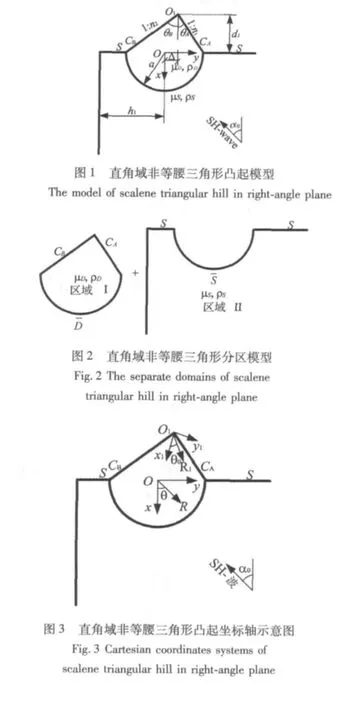
研究SH波对局部地形的散射问题，不仅具有理论价值而且在实际工程中具有非常广泛的应用前景。近几十年里，人们做了大量的研究并取得了许多有价值的研究成果［1－5］。凸起地形或结构对地震动的影响也一直是地震工程学中的重要研究课题，主要包括圆弧形凸起、含圆形孔洞的半圆形凸起及三角形凸起［6－8］。其中对三角形凸起结构的研究空间主要集中在弹性半空间，对直角域中含三角形凸起地形或结构的研究却很少见。本文利用复变函数及移动坐标技术研究了直角域非等腰三角形凸起对SH波的散射问题，并给出了本问题的解析解。该问题与以往半空间问题的最大区别在于垂直边界的出现，当弹性波入射时，将导致弹性波在直角域自由表面及缺陷附近产生多次的散射和反射，使得满足直角域自由边界的应力自由条件的散射波场解析表达式很难给出，因此为了解决这一难题，本文引入“镜像”叠加原理构造满足需要的散射波场。同时求解该问题时，主要采用“分区”的思想，将理论模型划分为两个区域，区域Ⅰ为含有半圆形弧底的非等腰三角形凸起，区域Ⅱ为含有半圆形凹陷的直角平面区域。其中关键问题是构造区域Ⅰ中满足三角形凸起两斜边应力自由的驻波解答和构造区域Ⅱ中由半圆形凹陷引起的满足直角域两自由边界的散射波表达式。最后给出地表位移幅值的具体算例，讨论了入射角度，入射波数以及直角域垂直边界等因素对地表位移幅值的影响。

1 基本理论

1.1 理论模型

图1所示SH波入射直角平面区域中含非等腰三角形凸起模型，入射角度为α0。非等腰三角形凸起的定点为O1，两斜边分别用CA和CB表示，其斜度分别为1∶n1和1∶n2，凸起高度为 d1，底边中点记为 O，O 点距O1在三角形底边上投影距离为，坐标原点O到直角域垂直边界距离为h1。介质Ⅰ材料的密度和剪切弹性模量分别为ρD和μD，介质Ⅱ材料的密度和剪切弹性模量分别为ρs和μs。

该问题属于混合边值问题，为此采用“分区”思想求解，即将整个求解区域分割成两部分来处理，如图2所示。区域Ⅰ为含有半圆形弧底的非等腰三角形，区域Ⅱ为含有半圆形凹陷的直角域。

如图3所示，分别以三角形底边中点O和三角形顶点 O1为坐标原点建立坐标系 xoy和 x1o1y1，其中o1x1为顶点的平分线。

1.2 基本方程

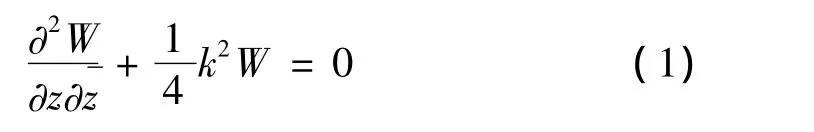
其中，k=ω/cs为波数，ω为位移函数圆频率，cs=是介质的剪切波速。

相应的应力表达式为:

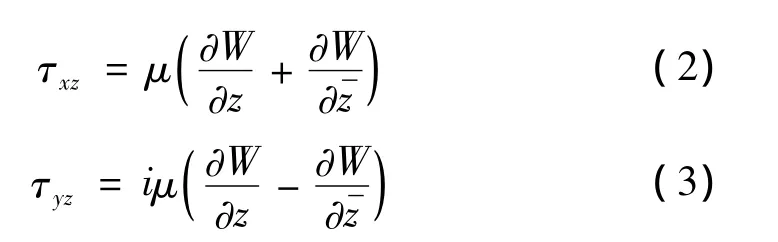
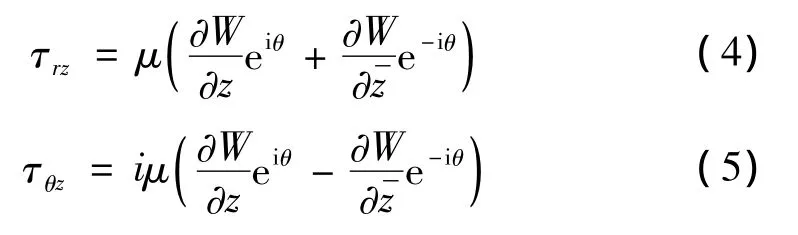
1.3 辅助函数Ⅰ

在区域Ⅰ内构造一个驻波解，使其满足圆弧形上位移、应力不受约束，且满足如下边界条件:

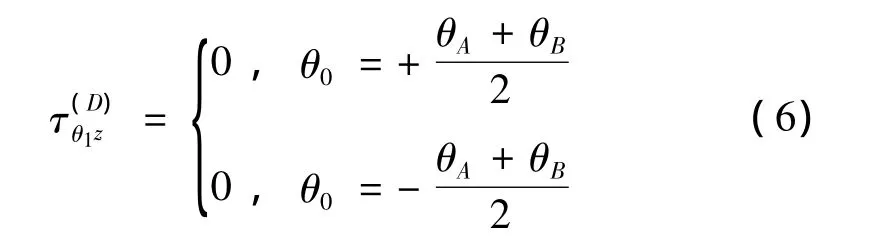
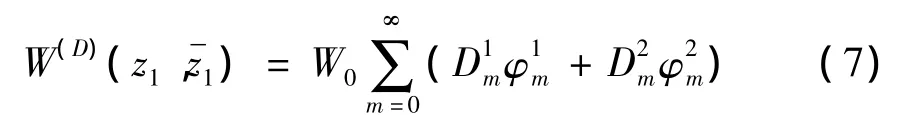
其中:

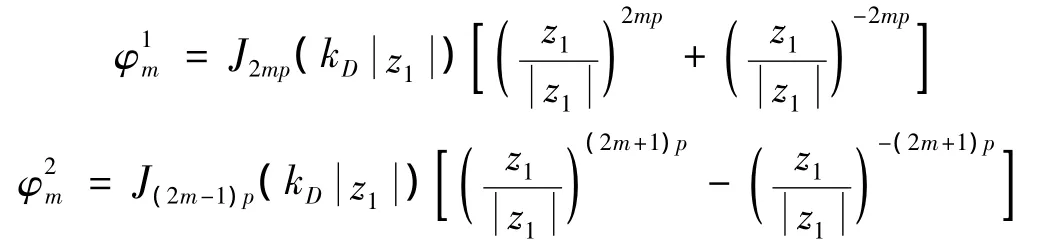
式中:W0为驻波的最大幅值，D1m，D2m为待求常数，同

则满足控制方程及上述边界条件的位移函数可以写成［9］:时分别为 2mp，(2m+1)p阶Bessel函数。由于 z1=(z+d1)eiq，q=(arctann2－，则利用坐标移动技术，上述驻波解在复平面上的表达式为:

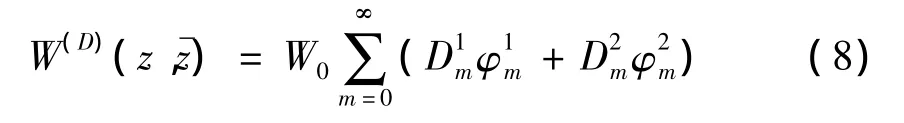
其中:

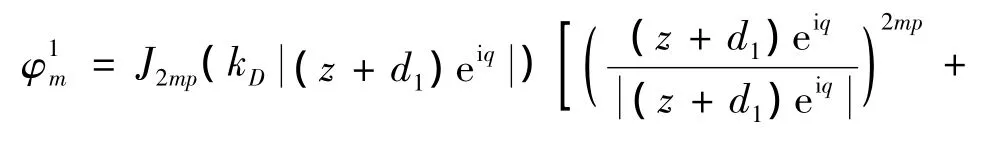
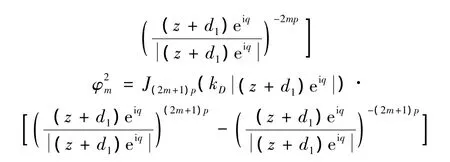
式(8)相应的应力表达式为:

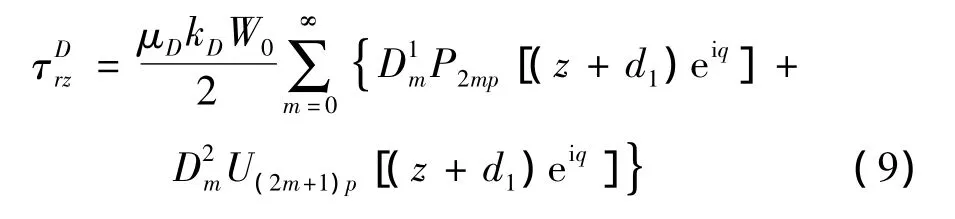
其中:

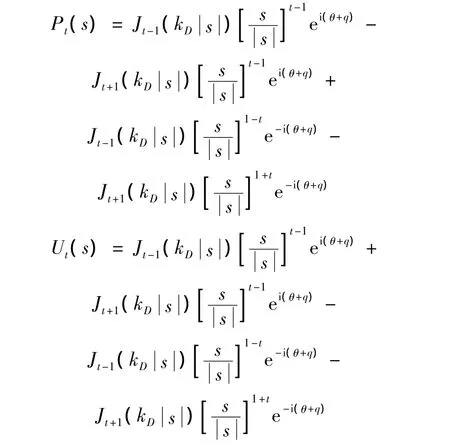
1.4 辅助函数Ⅱ

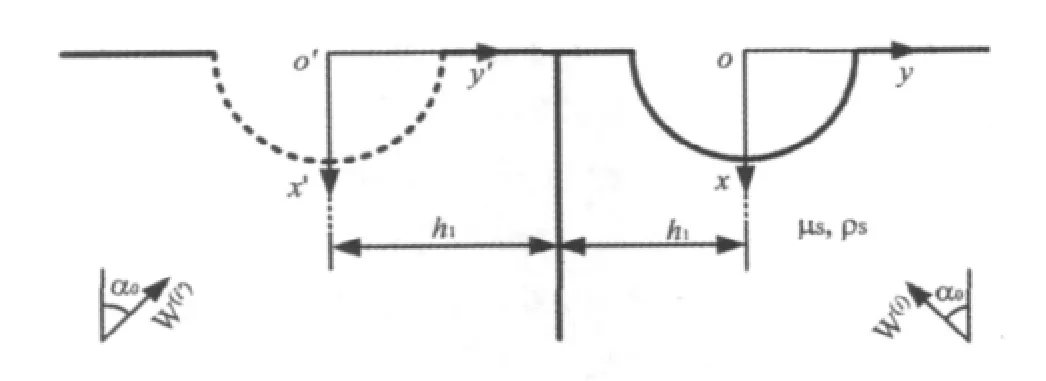
图4 镜像模型Fig.4 The model of“image”

求解本文问题的关键在于散射波表达式的构造，其需要满足控制方程(1)，同时要满足直角域边界Γ1、Γ2应力自由条件。因此采用文献［10］的“镜像”方法，把直角空间向走拓展为半空间模型，如图4所示。在区域Ⅱ中，构造的散射波W(s)如下:

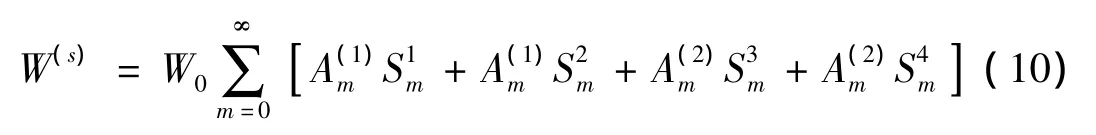
其中:

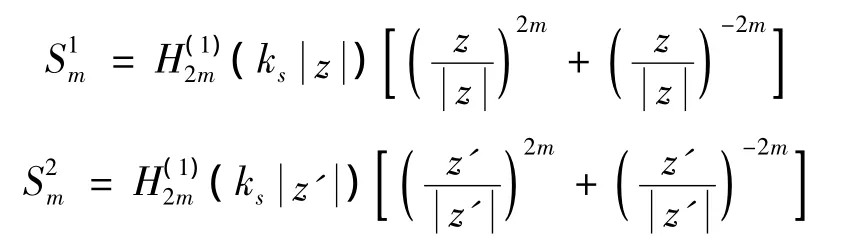
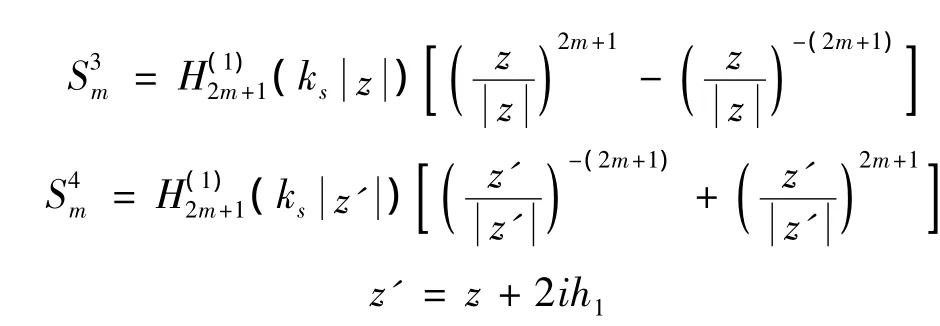
相应的应力可以表示为:

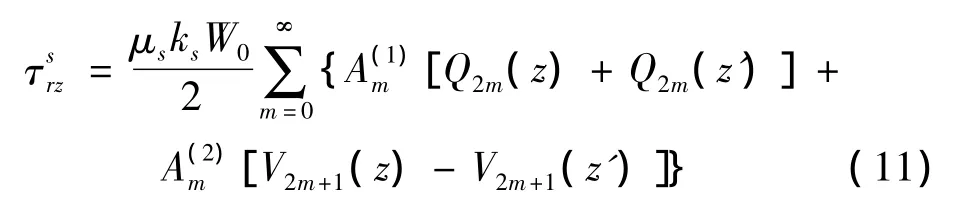
其中:

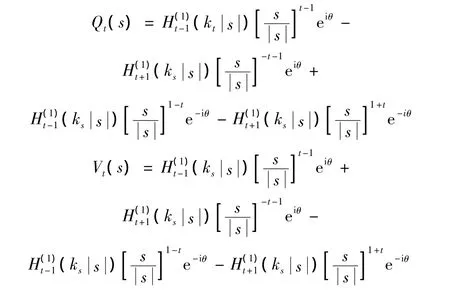
1.5 入射波与反射波

入射波与反射波在弹性半空间的表达式可以表示如下:

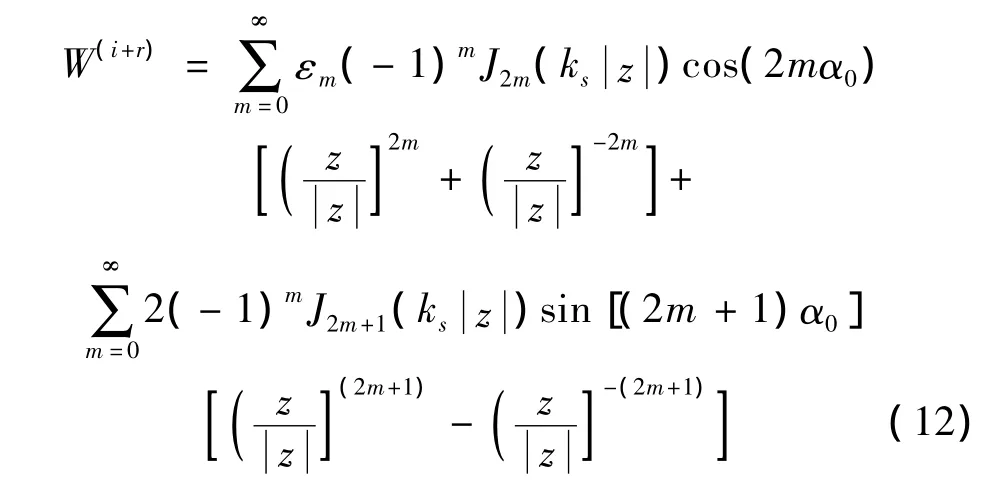
其中:假设入射波最大幅值 W0=1。当m=0时，εn=1，当m ＞1时，εn=2。

然而，在直角域中入射波与反射波将在其两个垂直边界上发生多次反射，为了满足直角域边界应力自有条件，仍然采用“镜像”方法构造等效的位移表达式，在复数坐标系)下，上式可以表示为:

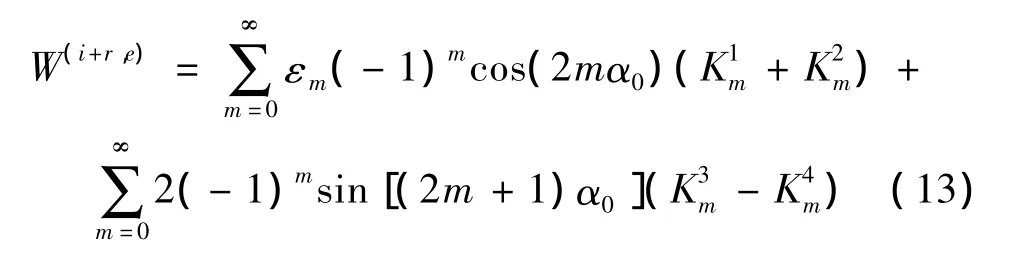
其中，

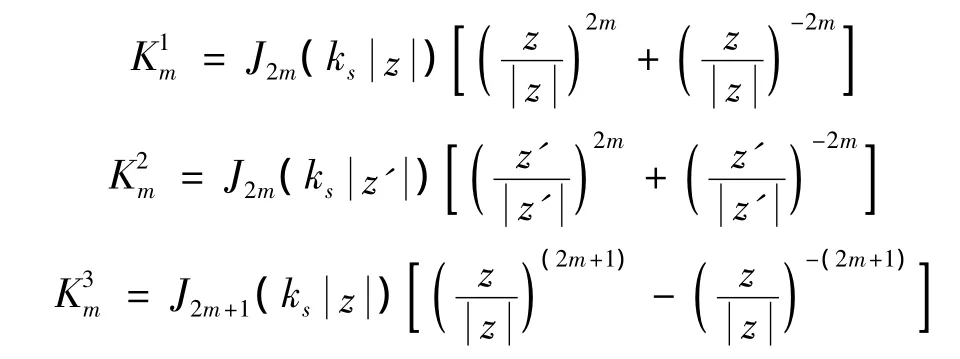
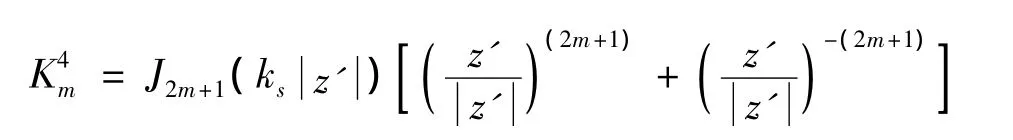
相应的应力表达式如下:

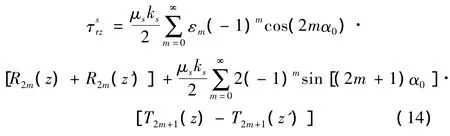
其中:

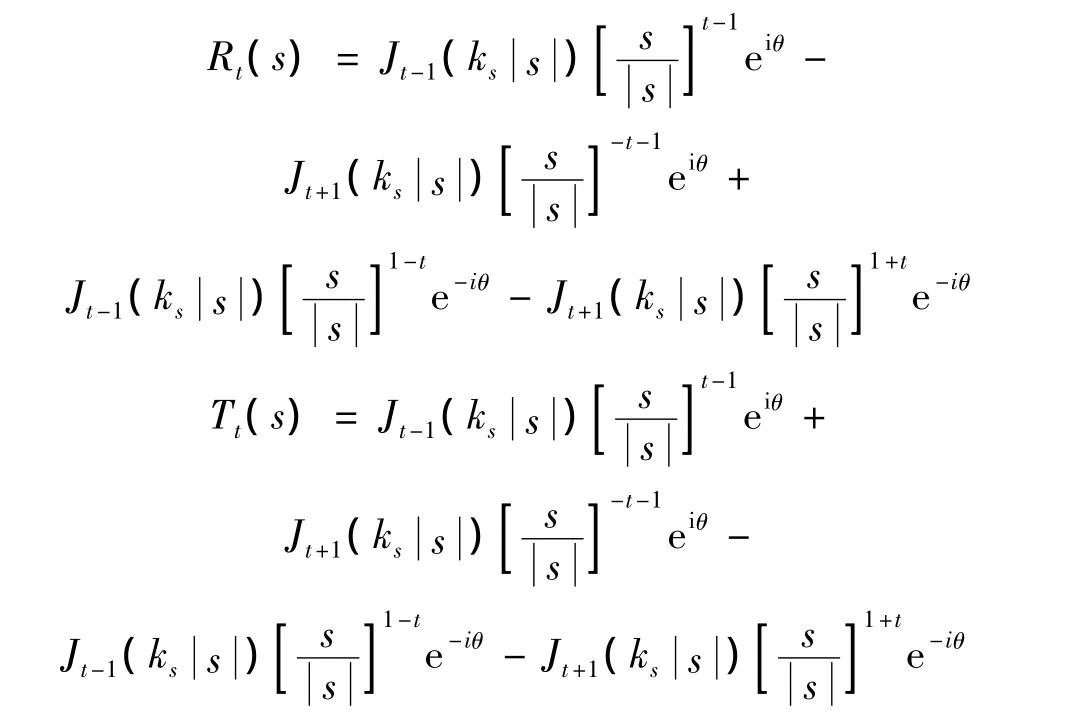
1.6 定解积分方程组

利用区域Ⅰ、Ⅱ公共边界S上位移、应力连续性条件，有:

2 地表位移幅值

在区域Ⅰ中的总波场为W(D)，而在区域Ⅱ中的总波场为:

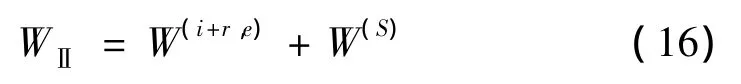
上式可以写成:

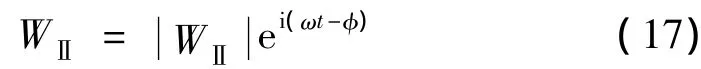
同时，入射波数表示为:

其中:λ为入射波波长，或者写成:

3 算例分析与讨论

当区域Ⅰ和区域Ⅱ介质完全相同时，即kD=kS，μD=μS，问题就转换为直角域含非等腰三角形凸起地形对SH波的散射问题。当区域Ⅰ和区域Ⅱ介质不同时，即kD≠kS或μD≠μS，问题就转换为直角域含非等腰三角形凸起坝体结构和基础的相互作用问题。

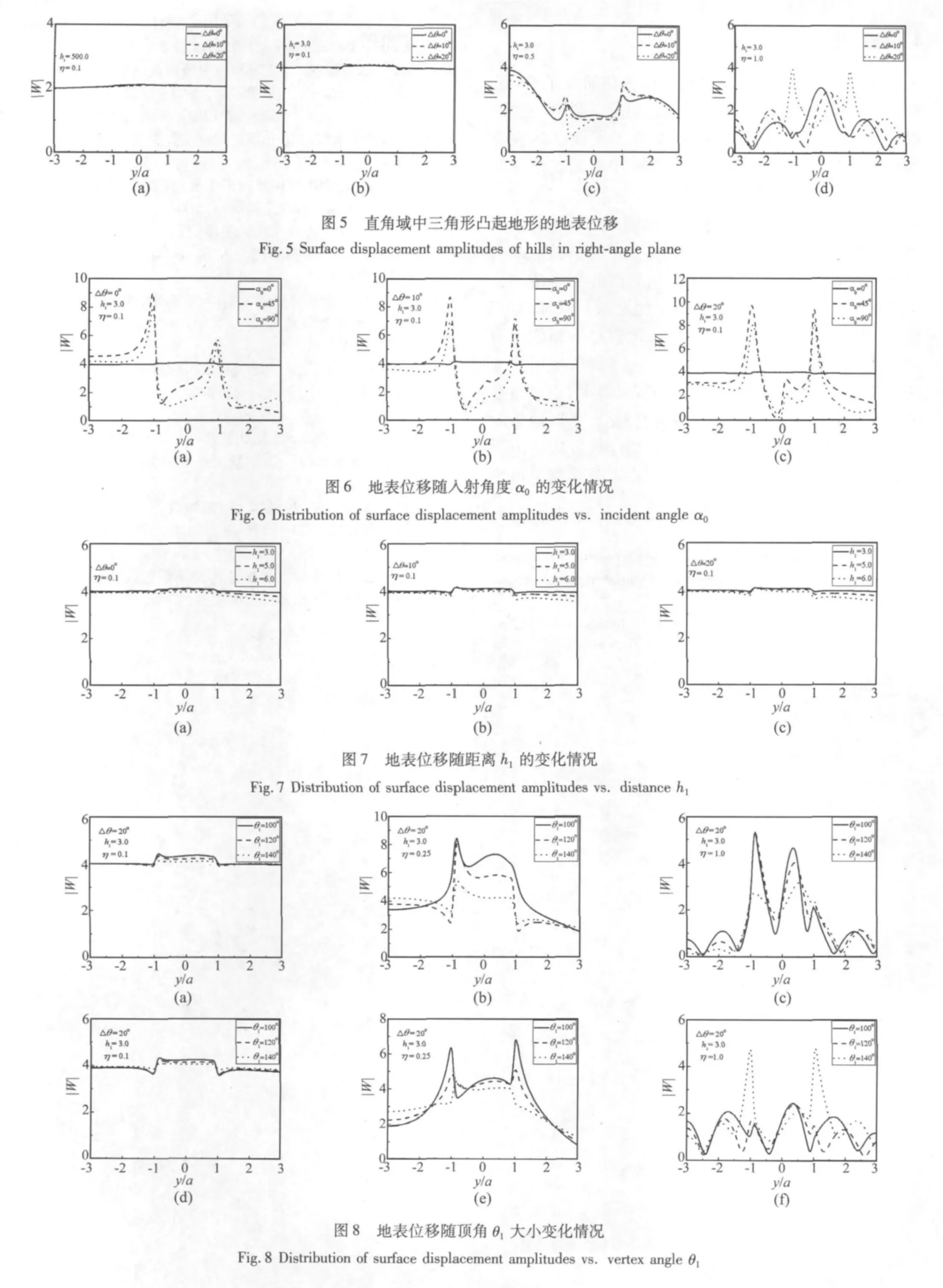
(1)图5给出了当SH波以角度α0=0°入射时，地表位移的变化情况。材料参数μD=μS=0.1。当h1足够大时(本文取h1=500.0时)，直角域含三角形凸起地形问题可近似看成半空间中含三角形凸起地形问题。当入射波数η=0.1，三角形凸起地形顶角θ1=θA+θB=138.2°一定且 Δθ= θB－ θA=0°，10°，20°时，图5(a)所示图形与文献［11］相符，由此说明本文方法的正确性。而图5(b)～图5(d)给出当三角形凸起顶角θ=140°一定，Δθ= θB－ θA=0°，10°，20°且 h1=3.0，η =0.1，0.5，1.0，2.0 时地表位移的变化情况。由图 5(b)可以看出，当SH波以η=0.1入射时，即准静态情况，地表位移幅值变化并不明显，显示出一定的静态特性，而由图5(c)～图5(d)可以看出，随着入射波数的增加，图形的变化越来越明显，显示出动态特性。同时，由于直角平面垂直边界的影响，靠近直角域垂直边界一侧的地表位移幅值要大于另一侧，这说明直角域垂直边界的影响也应给予考虑。对于Δθ=0°情况时，相当于是等腰三角形凸起地形问题，一般情况下，其地表位移幅值小于非等腰三角形凸起地形情况。

(2)图6给出了直角域非等腰三角形凸起地形地表位移幅值随入射角度α0的变化情况。三角形凸起顶点 θ1=140°一定，μD= μS=0.1，入射波数 η =0.1。图6(a)～图6(c)分别对应 Δθ=θB－θA=0°、10°、20°情况。由图中可以看出，当α0=0°时，地表位移最大值一般出现在三角形凸起位置处，而当入射波以45°或90°入射时，地表位移最大值发生偏移，一般发生在三角形凸起与水平表面相接处。由此说明了入射角度影响地表位移的分布情况。

(3)图7给出了直角域非等腰三角形凸起地形地表位移随距离h1的变化情况。三角形凸起顶点θ1=140°一定，μD= μS=0.1，入射波数 η =0.1，入射角度α0=0°。图7(a)～图7(c)分别对应 Δθ=θB－θA=0°，10°，20°情况。由图中可以看出，随着距离 h1的增加，地表位移幅值变小。

(4)图8给出了直角域含非等腰三角形坝体结构时地表位移随三角形顶角θ1的变化情况。这里Δθ=20°一定，入射角度α0=0°，h1=3.0，η =0.1。图8(a)～图8(c)对应取材料参数 ρD/ρS=2/3，μD/μS=1/6即坝体结构相对基础较软情况。图8(d)～图8(f)对应取材料参数 ρD/ρS=3/2，μD/μS=6 即坝体结构相对基础较硬情况。由图中可以看出三角形坝体结构对地表位移的影响要比三角形凸起地形情况地表位移变化明显。同时，随着入射波数的增加，地表位移同样显示出动态特性。

4 结论

本文利用复变函数及多极坐标方法研究了SH波对直角域非等腰三角形凸起的散射问题。利用“镜像”思想推导了本文所需解析解表达式，并给出了地表位移幅值的算例分析。通过具体算例，了解到直角域非等腰三角形凸起地形受入射波数，入射角度，三角形凸起夹角以及原点到直角域垂直界面距离的影响。非等腰三角形凸起地形地表位移变化要比等腰三角形凸起地形位移变化复杂，而非等腰三角形凸起坝体结构位移变化比三角形凸起地形位移变化复杂。同时，当三角形坝体结构相对基础较软时，其地表位移幅值大于坝体结构较硬情况。需要指出的是，本文所采用的方法在理论上是没有问题的，但当编程计算时，当三角形顶角取小于60°时，计算精度却很差，反而当顶角角度越大时，其计算精度越高。故本文的计算方法适用于非等腰三角形顶角大于60°情况。同时，算例结果可为实际工程等领域提供理论参考。

［1］ Trifunac M D.Scattering of plane SH-waves by a semicylindrical canyon［J］.Earthquake Engineering and Structure Dynamic，1972，1(3):267－281.

［2］ Lee V W，Manoogian M E.Surface motion above an arbitrary shape underground cavity for incident SH wave［J］.European Earthquake Engineering，1995，8(1):3－11.

［3］ 林 宏，刘殿魁.半无限空间中圆形孔洞周围SH波的散射［J］.地震工程与工程振动，2002，22(2):9－16.

［4］ 齐 辉，王 艳，刘殿魁.半无限空间界面附近SH波对圆形衬砌的散射［J］.地震工程与工程振动，2003，23(3):41－46.

［5］ 陈志刚，刘殿魁.SH波冲击下浅埋任意形孔洞的动力分析［J］.地震工程与工程振动，2004，24(4):32－36.

［6］ 刘 刚，刘殿魁.SH波对浅埋圆形弹性夹杂附近任意三角形凸起地形的散射［J］.应用力学学报，2007，24(3):373－379.

［7］ 刘 刚，刘殿魁.SH波入射时浅埋圆孔附近等腰三角形凸起地形的地震动［J］.固体力学学报，2007，28(1):60－66.

［8］ 邱发强，王慧文，王 雪.SH波入射时非等腰三角形结构与基础相互作用［J］.哈尔滨工业大学学报，2010，42(4):634－638.

［9］ 邱发强，刘殿魁.SH波对等腰三角形凸起地形散射问题中的驻波函数［J］.哈尔滨工程大学学报，2007，28(5):525－528.

［10］ 折 勇，齐 辉，杨在林.SH波对直角平面区域内圆形孔洞的散射与地震动［J］.应用力学学报，2008，25(3):392－397.

［11］ 邱发强.SH波对三角形凸起及其附近浅埋圆孔的散射［D］.哈尔滨:哈尔滨工程大学，2006，53－58.