非等时距Verhulst修正模型及其在直升机故障率预测中的应用

张宏斌，曹学峰，孙世霞，王进才

(陆军航空兵学院航电和兵器工程系，北京 101114)

0 引言

可靠性、维修性定量要求是影响装备可靠性、维修性的关键因素之一，它直接关系到系统的效能和全寿命周期费用的优劣［1］。因此，对于新机可靠性研究而言，可靠性指标定量的确定具有重要意义。

直升机累计故障率是表征直升机可靠性的一个重要指标。累计故障率的大小直接反映了直升机可靠性的高低，可以为维修计划、训练保障、器材供应等装备管理工作提供参考依据。但是，在目前直升机可靠性研究工作中，尤其是新装备部队的机型，其可靠性数据不易获得，且数据量极少。同时，影响直升机累计故障率的因素众多，各因素间的关系也无法确定。由此造成了新型直升机累计故障率预测过程中小样本、贫信息的问题。

灰色系统理论［2］是由我国学者邓聚龙教授于1982年创立的一门学科，该理论以“小样本、贫信息”不确定系统为研究对象，通过将灰色信息转化为白色信息提取有价值的数据，实现对系统的正确认知。随着灰色理论的不断发展，灰色理论被广泛地应用于产品寿命预测［3］、故障间隔时间预测［4］等工作中。同时，随着灰色理论应用范围的不断扩大，一些新的问题也随之产生，特别是针对非等距问题［5－7］，已经有多位学者进行了研究，并取得了一定的成果。

但是，直升机累计故障率预测具有其自身特点:1)故障率分布不同于GM(1，1)模型曲线;2)故障间隔时间不等，且跨度较大，而GM(1，1)模型在长期预测情况下误差较大［8］;3)随着故障间隔时间的增长，累计故障率终值将会趋近于1，而GM(1，1)模型终值是趋于发散的。

综上，本文针对直升机累计故障率预测特点及灰色理论应用中出现的问题，提出了直升机累计故障率预测非等距Verhulst修正模型。首先对Verhulst模型原始数据进行等距处理，然后根据预测结果为模型添加预测误差修正项，从而实现对直升机累计故障率的准确预测。

1 Verhulst模型原型

Verhulst模型具有如下特点:

1)要求原始数据为“S”型;

2)要求原始数据是等间隔的;

3)预测结果最终趋于一个恒值。

Verhulst模型的表达式为:

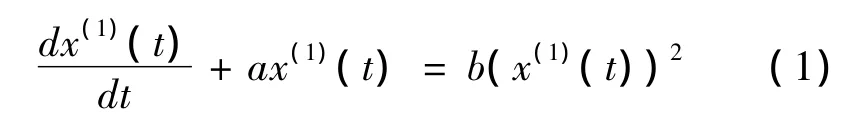
式中:a—常数，代表发展系数;b—常数，代表灰色作用量。

模型的解为:

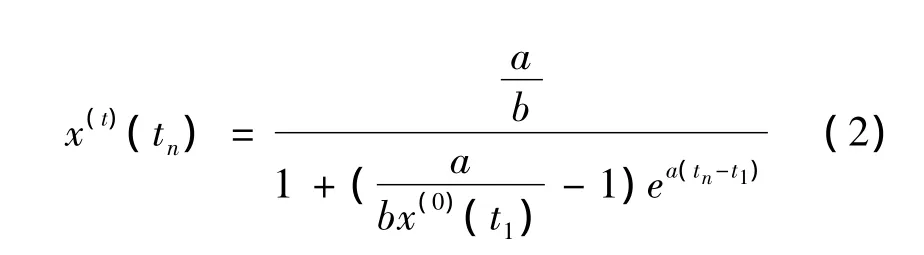
式中:x(0)(t1)—x(1)(tn)的初始值;t1—初始时刻。

由式(2)可见，Verhulst模型的解x(1)(tn)随时间tn变化呈“S”型，在开始端x(1)(tn)由初值x(0)(t1)随时间tn增长而缓慢增长，中间段增长较快，在末端随着tn→+∞，x(1)(tn)，将会达到一个恒定值——灰色发展系数:a/b。具体如图1所示。

图1 Verhulst模型曲线

该曲线与直升机累计故障率曲线相近。因此，可以应用Verhulst模型进行直升机累计故障率预测。但是，由于直升机累计故障率统计特点及Verhulst模型对原始数据的要求，需要对Verhulst模型进行改进才能实现对直升机累计故障率的准确预测。

2 非等距Verhulst修正模型

针对Verhulst模型在非等距预测中的应用问题已经有多位学者进行了研究，如:偶昌宝等［9］通过在区间上求积分对灰色背景值求取方法改进实现了对非等时距沉降量的预测;胡威等［10］则通过增加系数项对灰色背景值求取进行改进，对未来网络安全形势进行了预测;邓成发等［11］通过增加时间影响因子实现了对面板堆石坝沉降的预测。但是，上述方法在应用过程中需要经过大量计算，且模型比较复杂。因此，本文提出了一种对原始数据序列进行等距化处理，然后通过误差修正进行直升机累计故障率预测的非等时距Verhulst修正模型。

2.1 非等时距原始数据序列等距处理

设t1，t2，…tn为直升机故障间隔时间序列，记f(1)(ti)，i=1，2，…，n为其对应的直升机累计故障率观测序列，且ti+1－ti≠ti+2－ti+1，i=1，2…n。可见，直升机累计故障率序列为非等时距序列。

下面对原始数据序列进行等距处理。

设时间序列平均间隔值为:

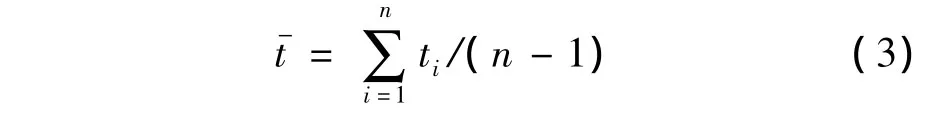
设αi为时间序列间隔权重，则有:

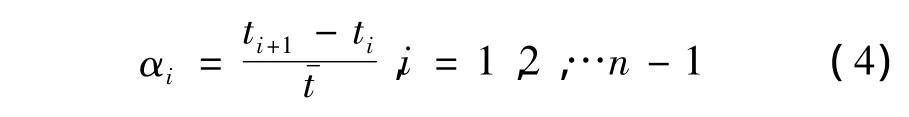
时间序列变为:

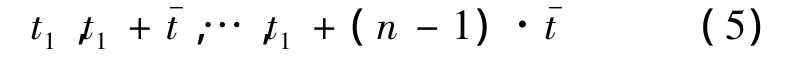
根据时间序列间隔权重对对应的直升机累计故障率观测序列进行等距处理:

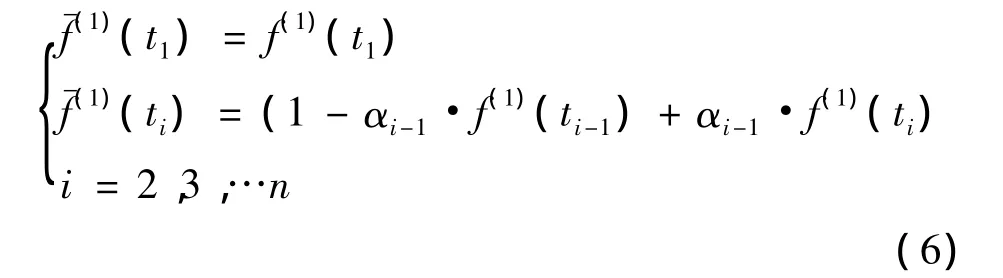
因为直升机累计故障率原始数据序列曲线与Verhulst模型曲线相近，即已经符合“S”型，因此按照Verhulst模型建模方法，取原始数据序列为:f(1)(ti)，i=1，2，…n。

其1－IAGO序列为f(0)(ti):

其灰色背景值:

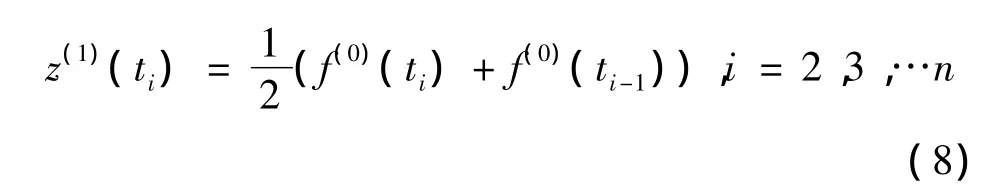
应用最小二乘法求取非等时距Verhulst模型参数序列:

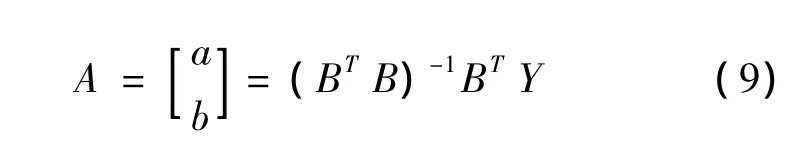
式中:a—白化系数(发展系数);b—灰色作用量。

且构造:

通过对非等时距Verhulst模型求解可得:

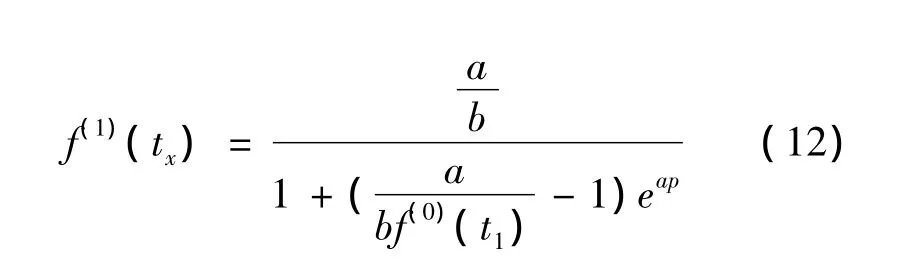
2.2 误差修正项的确定

由式(12)可见，随着故障间隔时间tx增长，非等时距Verhulst模型终值趋近于灰色发展系数:a/b，而直升机累计故障率终值趋近于1，这就意味着a/b将直接影响到非等时距Verhulst模型长期预测的精度，且最终误差为:1－a/b。为此，需要对非等时距Verhulst模型进行修正。

任何预测模型在短期预测内误差一般较小，随时间不断增长，预测误差也将不断增大，因此本文以时间为误差修正系数因子构造非等时距Verhulst模型预测误差修正系数f′。

即:

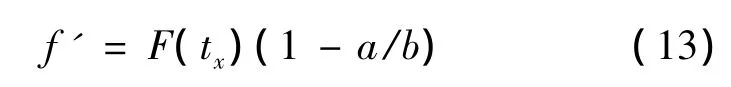
式中:F(tx)—故障间隔时间tx的函数。

且F(tx)∈［0，1］，即在时间序列最初点处修正误差为0，而在故障间隔时间趋于无穷大时修正误差达到最大值1－a/b。

按上述要求构造F(tx)有:

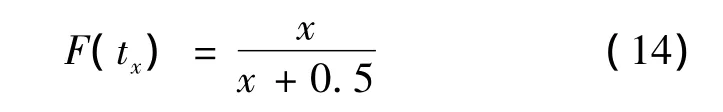
则修正后的非等时距Verhulst模型解为:

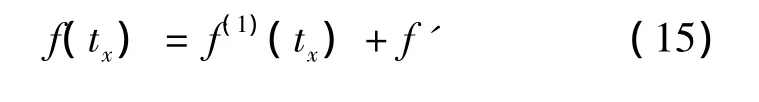
3 实例

表1中的数据是从参考文献［12］中提取的某型直升机累计故障率数据。

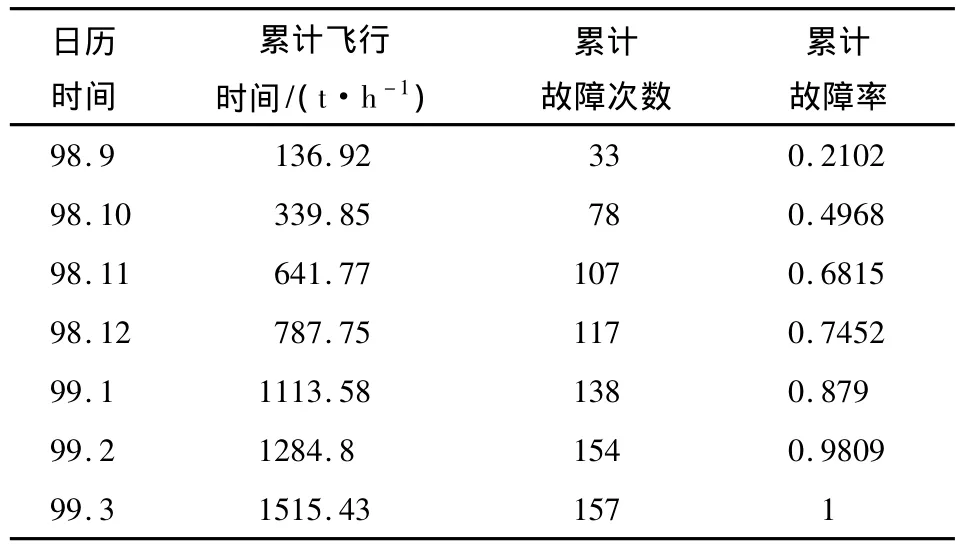
表1 某型直升机累计故障率数据

由表1可见，某型直升机故障间隔时间为非等时距序列。且其累计故障率曲线与Verhulst曲线相近。因此，应用本文所提出的方法进行故障率预测。

由式(4)可得平均故障间隔时间为:

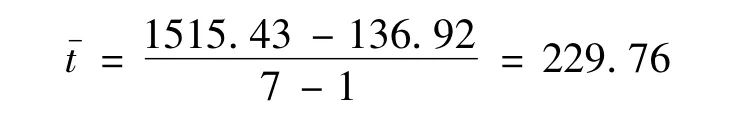
按式(5)、式(6)对原始数据序列进行等距处理后，建立非等时距Verhulst模型并取前5个数据作为原始数据序列进行建模及预测。

可求得模型参数:

a= －1.0425，b= －1.1138。

则:a/b=0.94。

由式(13)可得误差修正系数为:

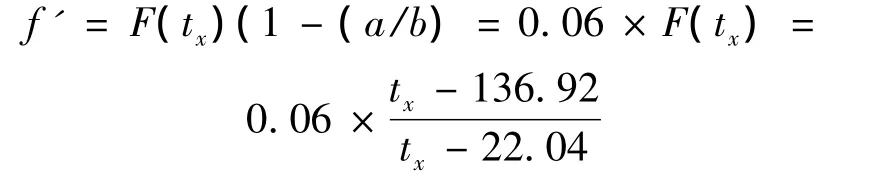
非等时距Verhulst模型及非等时距Verhulst修正模型对原始数据序列拟合、预测结果见表2，拟合比较曲线如图2所示。

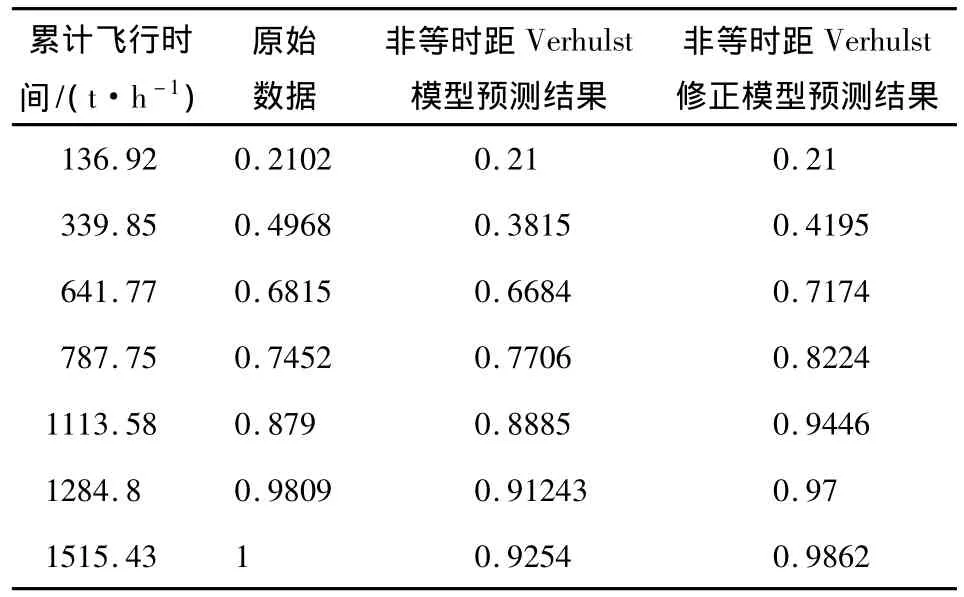
表2 非等时距Verhulst模型及非等时距Verhulst修正模型预测结果比较

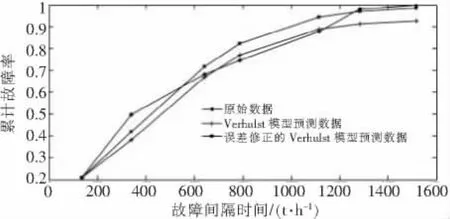
图2 非等时距Verhulst模型及非等时距Verhulst修正模型拟合曲线比较

由表2数据可见，非等时距Verhulst模型平均预测精度达到了93.69%，非等时距Verhulst修正模型平均预测精度达到了94.1%，精度相差不多。但是在长期预测过程中，例如故障间隔时间为1284.8小时和1515.43小时时，非等时距Verhulst模型预测精度为92.78%，而非等时距Verhulst修正模型预测精度为:98.75%，要高于非等时距Verhulst模型。同时，当故障间隔时间进一步增长，直升机累计故障率将趋近于1，而非等时距Verhulst模型预测精度势必进一步降低。

4 结论

1)非等时距Verhulst修正模型通过对原始数据序列的时间序列求取平均值，并以此确定等时距处理时的权重，实现了Verhulst模型在非等时距预测中的应用。

2)根据Verhulst模型终值趋于灰色发展系数，而直升机故障率终值趋于1的特点，通过对非等时距Verhulst模型添加预测误差修正项，提高了模型预测精度，解决了模型终值趋于灰色发展系数的局限性，对于中长期预测具有重要的意义。

3)通过本文实例可见，本文所提方法具有结构简单，初始数据易于处理，预测值无需还原计算，中长期预测精度较高等特点。该方法还可应用于其他具有累计故障率相似分布形式的装备、产品累计故障率预测中，为“小子样、贫信息”系统累计故障率预测提供了一种新的方法。

［1］王自力.直升机可靠性、维修性指标研究［J］.航空学报，1995，16(增刊):20 －27.

［2］邓聚龙.灰色系统基本方法［M］.武汉:华中理工大学出版社，2005.

［3］韦康男，姚立纲，吴志欢.给予灰色理论的产品寿命预测研究［J］.计算机集成制造系统，2005，11(10):1491－1495.

［4］高鸣，唐双喜，徐廷学等.基于灰色理论的导弹装备故障间隔时间预测［J］.海军航空工程学院学报，2008，23(3):343－345.

［5］戴文战，李俊峰.非等间距GM(1，1)模型建模研究［J］.系统工程与理论实践，2005，9:89 －93.

［6］Luo You－xin，Chen Mian－yun，Che Xiao－yi etc.Non－equal－interval direct optimizing Verhulst model that x(n)be taken as initial value and its application［J］.Journal of Southeast University(English Edition)，2008，24(Sup):17－21.

［7］郭丽萍，孙伟，郑克人，等.非等时距GM(1，1)直接模型及其在材料试验数据处理中的应用［J］，东南大学学报(自然科学版)，2004，34(6):833 －837.

［8］何必高，刘福太.弹上电子设备可靠性灰色预测方法［J］.舰船电子工程，2008，28(3):160 －161，172.

［9］偶昌宝，俞亚南，王战国.不等时距灰色Verhulst模型及其在沉降预测中的应用［J］.江南大学学报(自然科学版)，2005，4(1):63 －65.

［10］Hu Wei，Li Jian－hua，Chen Xiu－zhen etc.Network security situation prediction based on improved adaptive grey verhulst model［J］.Journal of Shanghai Jiaotong U-niversity，2010，15(4):408 －413.

［11］邓成发，戴春华，周苏波.基于修正Verhulst模型的面板堆石坝沉降预测［J］.水电自动化与大坝监测，2010，34(3):53 －56，64.

［12］陈圣斌，周晓光，陈大禄.基于神经网络的直升机可靠性预计［J］.直升机技术，2009，3:31－34.