考虑热－结构耦合关系下空间结构动力响应随机性分析

阎 彬，陈建军，马洪波，靳红玲

(西安电子科技大学 电子装备结构设计教育部重点实验室，西安 710071)

空间结构的主要热交换形式为热辐射及结构内的导热，而无对流，在其工作过程中受到太阳照射的持续热流。结构在照射面和背阴面产生的截面温差作用，将导致结构的热变形。考虑结构热变形会改变光照入射角度，从而影响结构表面的温度分布，而温度的分布差异又会使截面温差产生影响，进而影响结构变形，从而产生了热－结构之间的耦合关系。另一方面，结构温度的变化使得结构的各项参数都有不同程度的改变，体现出一定的随机性，故有必要考虑参数随机性的影响。综合考虑上述因素的空间结构的热响应情况，将使分析结果更为准确，并可为空间结构的热疲劳可靠性预测奠定基础。

目前航天器等空间结构主要采用薄壁圆管构件。文献［1－2］给出了一种同时考虑截面平均温度和截面温差的薄壁圆管有限单元模型，可同时分析结构热轴力和热弯矩，并应用于哈勃望远镜太阳能帆板的算例中。文献［3］在文献［1］的基础上考虑了热变形与温度的耦合关系，但基于在温度变化范围内，结构参数不变化的假定。实际中空间结构由于温变其参数必然发生改变，只是这些变化是微小的，但对于高精度的设备结构，这种由于温变而导致的结构参数变化将是不容忽略的。文献［4－5］分析了梁结构在热载荷作用下的动力响应问题。文献［7－9］先后对多种结构的随机响应问题进行了研究，并获得了随机参数对响应的影响。在目前诸多的研究成果中，空间结构在热载荷下的动力响应分析已有相应文献，但针对其随机性分析的工作尚鲜见，故寻求一种简单有效的空间结构在热载荷下的随机性分析方法是十分必要的。

本文基于以上研究成果，综合考虑热－结构耦合效应和参数的随机性，对空间薄壁圆管的温度场及动力响应进行求解，利用基于灵敏度分析的矩法和随机因子法推导出结构温度和动力响应的数字特征计算表达式，分析了热－结构耦合效应对结构动力响应的影响，获得了各响应量均值和均方差的时间历程，并考察了各随机参数对温度、位移和应力响应分散性的影响，最后通过Monte-Carlo模拟法对计算结果进行验证。

1 空间结构热－动力学有限元模型的建立

1.1 考虑热－结构耦合关系的热传导有限元方程

以图1和图2所示的空间结构最常见的薄壁圆管为分析对象，该结构具有壁薄且轴向尺寸长的特点。据此特点和空间环境的热传导机理，在建立热传导微分方程时基于三点假定:① 辐射换热条件只考虑结构外表面对太空的散热，而忽略结构内壁间的换热;②结构截面平均温度远大于截面扰动温度;③ 忽略沿壁厚方向的导热，只考虑结构周向导热。考虑热－结构的耦合关系，即计及结构变形对表面接收热流量的影响。由图1几何关系可知，θz为结构变形后表面法线与竖直方向的夹角，其大小等于入射点处的截面转角θ=dw/(ldξ)，其中l为管长，w为入射点处横向位移，ξ=x/l为轴向x方向的无量纲化坐标。转角变化会导致入射热流量的改变，考虑图1位置处dw/dξ为负值，故S=S0cos［β－dw/(ldξ)］表示结构表面的净辐射热流量，S0为太阳辐射热流密度，β为光照入射角。据文献［1－2］和以上假定，考虑由太阳辐射的热量输入，结构向外的辐射散热，结构在轴向和周向的导热，以及热－结构的耦合关系，利用热辐射的Stefan-Boltzmann定律建立热平衡微分方程为:

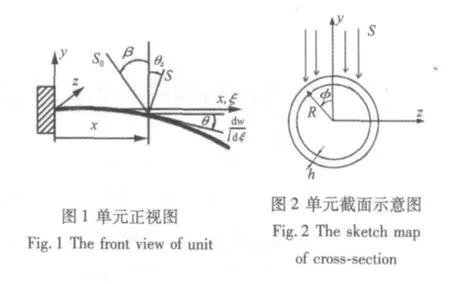
式中:R，h分别为圆管的半径和管壁厚，ρ为质量密度，c为比热容，ε为管外表面散射系数，T为管内的瞬态温度场，kφ、kξ分别为周向和轴向导热系数，αs为管外表面吸收系数，φ为管截面的周向角度，σ为Stefan-Boltzmann常数，δ为跟踪功能函数，反映了太阳光照射角度与照射表面间的关系，它取决于β、θz角，即有:

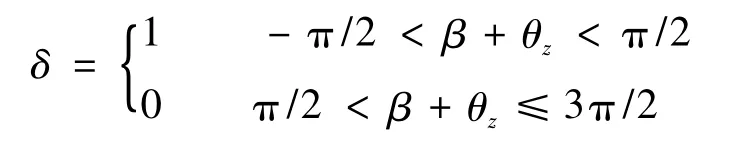
为了便于考察由管截面温差导致的热致振动，将管截面温度T分解为两部分之和:

其中:T0(ξ，t)为管截面内平均温度，T1(ξ，t)为管截面内最大扰动温度，两者都为轴向坐标和时间的函数。将式(1)中的温度非线性项T4在截面平均温度处一阶泰勒展开，即有:

将式(2)、(3)代入式(1)中，整理可得两个独立的分别由截面平均温度和截面最大温差为变量的微分方程，对此微分方程利用伽辽金方法沿轴向积分，可得到薄壁管的热传导有限元方程。圆管的有限元离散采用两节点Lagrange单元，每个节点有两个温度自由度，即截面平均温度和截面最大温差，其有限元方程式为:

其中各矩阵和向量表达式如下［1－3］:

式中:C为热容矩阵，KT为热传导的等效刚度矩阵，RT为与辐射相关的矩阵项，N为两节点Lagrange插值函数，B=dN/dξ为应变矩阵，m为单元数，Q0为变形前等效的热载荷向量，Q1由于包含dw/dξ项，为结构变形与温度场的耦合项。诸式中上角标为“0”者是以截面平均温度建立的有限元列式中的相关矩阵及向量，而为“1”者则对应于截面扰动温度部分。

对式(4)的求解分两部进行，由于R0T项的存在，使式(4a)成为非线性瞬态温度场问题。本文采用时间差分并结合牛顿内迭代的数值解法。首先对式(4a)利用Galerkin格式的时间差分将其展开为［10］:

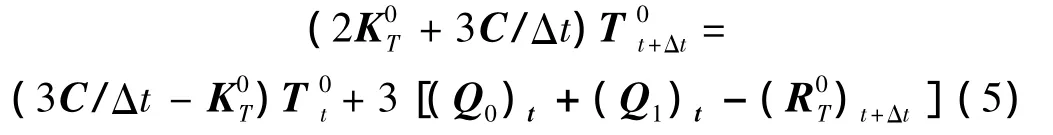
式中:Δt为时间步长，当已知t时刻平均温度T0t，且结构在t时刻的动力响应已得出，代入式(5)成为关于的非线性方程，利用牛顿内迭代法即可近似求解

对式(4b)，由于平均温度T0在t和t+Δt时刻都已知，故R1T即为已知，同样按照式(5)的形式展开，得到以T1t+Δt为待求变量的线性方程，直接利用时间差分法即可求解。

1.2 温度荷载下空间结构动力学有限元分析

将空间薄壁圆管结构作为Euler-Bernoulli梁，并离散为m个单元、m+1个节点。对该梁考虑轴向位移的动力学有限元方程为［6］:

式中，a=［u1w1θ1… um+1wm+1θm+1］T为结构节点位移向量，每一节点具有:轴向位移u、横向位移w和截面转角θ三个自由度;单元轴向位移由两节点Lagrange插值形函数N插值表示，单元横向位移则利用Hermite插值函数Nw;M，K和D分别为结构的质量矩阵、刚度矩阵和阻尼矩阵，在此采用 Rayleigh阻尼［2，6］，即取 D= α2M+ β2K，其中 α2、β2为 Rayleigh 阻尼系数，Pf、PT分别为结构节点力载荷向量和由温度引起的热载荷向量，M、K和Pf的表达式可由文献［6］得知，PT的表达式如下:

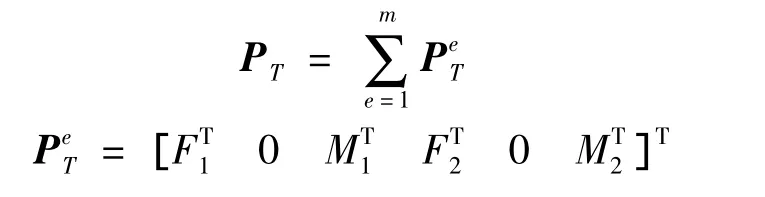
式中:E为弹性模量，α为线膨胀系数，T0为结构初始温度，FT为轴向热载荷，MT为热弯矩。

由上式可看出，轴向热载荷主要由截面平均温度产生，而热弯矩仅由截面扰动温度引起，两者分别产生的轴向位移和横向位移(包括截面转角)可以分开求解。

式(4)和式(6)共同构成了空间结构的热－动力学耦合有限元方程，对其求解须采用时间积分法在每个时间步处将温度场和动力响应交替迭代进行，这是一种在时间域内的近似数值计算方法，其中关于瞬态温度场的计算见1.1节，而对动力响应的求解则利用了Newmark积分法，具体求解步骤为:

(1)给定初始值，即t0时刻温度分布T0(t0)、T1(t0)，位移a(t0)，速度(t0)和加速度(t0)均为已知，并确定时间步长Δt;

(2)以Δt为时间步长，将T0(t0)、a(t0)代入 式(4a)，由于非线性项R0T，利用时间差分法即式(5)格式和牛顿迭代法计算得到T0(t0+Δt);

(3)将T1(t0)、T0(t0)、T0(t0+Δt)、a(t0)代入式(4a)，式(4b)为线性方程，直接利用时间差分求得T1(t0+Δt);

(4)利用已求得的T0(t0+Δt)和T1(t0+Δt)代入式(7)，得到温度载荷PT，结合a(t0)(t0)和(t0)对(6)式利用Newmark法进行动力响应计算，获得a(t0+Δt)、(t0+Δt)和·a·(t0+ Δt)。至此 t0+ Δt时刻的温度场及动力响应均已求出，继续重复(2)～(4)步即可得到各个时间步的温度场及动力响应;

2 结构响应随机性分析

在建立了上述确定性分析模型后，现将模型中的物性参数:质量密度ρ，弹性模量E，比热容c，热传导系数k，太阳光入射角度β，结构外表面散射系数ε，热吸收系数αs，热膨胀系数α等均视为服从正态分布的随机参数，则该模型成为含有随机参数的不确定性模型，需分别对温度场和动力响应的随机性进行分析。鉴于各自方程的不同特点和已有的研究成果，对两者随机性分析采用了不同的方法。

2.1 温度场随机性分析

将上述所有随机参数代入式(4)中，则式(4)成为含随机参数的有限元方程，对于其随机性分析，是以1.1节温度场求解方法为基础，利用求解随机变量函数数字特征的矩法进行分析，首先计算出温度对各物性参数的灵敏度，再根据矩法，即可获得温度场的均值和方差。

同前述瞬态温度场的求解顺序，先对平均温度的灵敏度进行分析。将结构物性参数记为ψ，从式(5)出发，两边对ψ求导，整理得:

式(8)即为平均温度灵敏度求解的递推迭代格式，其中:(·)'表示 ∂(·)/∂ψ，对变量 ψ 的灵敏度;为将中平均温度视为常数后，对ψ求偏导所得部分。式中各个矩阵和向量对ψ的偏导数由以下差分格式求得:

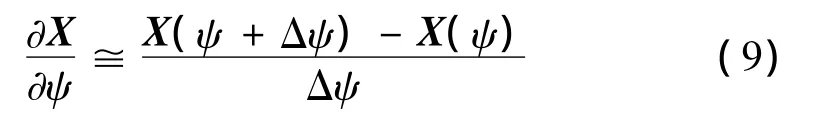
其中:X代表式中各相关矩阵和向量。

(1)对于各时不变矩阵及向量如K0T，C，Q0，可由式(9)计算出对ψ的灵敏度，由于它们与时间无关，故为常值，在迭代过程中只需计算一次。由于Q1和 R0T包含 dw/dξ和T0，故为时变向量和矩阵，其对ψ的偏导仍用差分法计算，只是在每个时间步都需重新计算一次。

(2)根据前述求解热－动力学耦合有限元方程的方法，已知t时刻的温度分布和动力响应，计算一步得到，代 入中 则为 已 知，仍可利用差分法计算出，此时为仅包含待求量'的矩阵，将前两步所得数据代入式(8)则可计算出

在得到温度场T0和T1对各随机变量的灵敏度后，则可利用矩法［8］求得温度场的数字特征，推导得其均值和方差的计算表达式为:

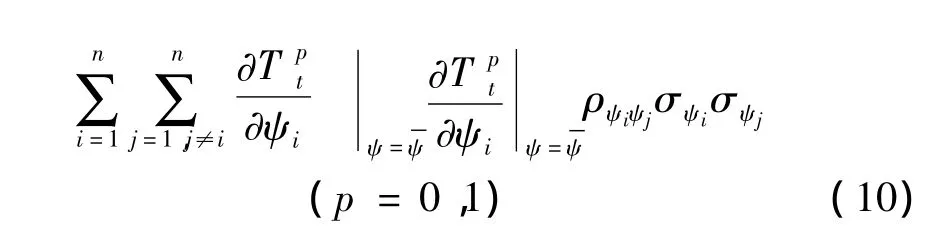
2.2 动力响应随机性分析

对于动力响应随机性分析，与温度场随机性分析相似，同样从方程的求解格式出发，利用随机因子法推导得到响应的数字特征表达式。首先给出利用Newmark法求解动力响应的计算公式，再将各随机参数以随机因子的表示形式代入，利用求解随机变量函数数字特征的代数综合法，导出位移响应的均值和方差。

考虑到空间环境下热载荷为主要载荷，故在本文中仅考察热载荷下结构的动力响应，重点分析在热弯矩作用下结构的横向位移及截面转角，此时结构节点位移向量为 w=(0，w1，θ1，…，0，wm+1，θm+1)T，相应的式(6)中各矩阵向量的形式都有所改变，只是将各矩阵向量中对应轴向位移部分都取为0即可。利用Newmark法对式(6)求解，即将其转化为如下拟静力迭代方程求解:

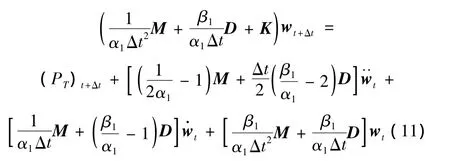
式中:α1和β1为精度和稳定性要求的可调参数，取α1=0.25，β1=0.5［10］时格式为无条件稳定。

利用随机因子法［7－8］，将所有随机参数均以随机因子形式表达，即令:E=，其余随机参数表示类似，其中:(·)*项为随机因子，其均值为1，变异系数为 ν(·)=均方差/均值;)项为随机参数的均值即名义值。

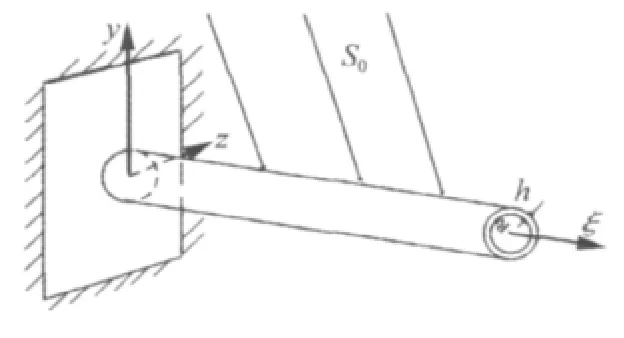
图3 悬臂薄壁圆管梁Fig.3 Thin-walled cantilever beam of circular cross-section

利用代数综合法对式(12)两边分别求均值和方差，可得位移响应在 t+Δt时刻的均值 μwt+Δt和方差分别为:

在得到位移响应后，不考虑由轴向位移导致的轴向应变，根据单元节点位移与单元应力之间的关系，可得结构轴向正应力为:

将式(15)中的随机参数以随机因子形式表示，则单元轴向正应力Seeξ可表示为:

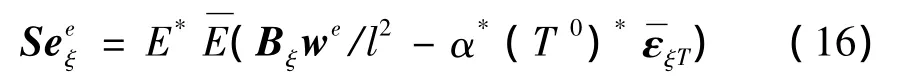
对式(16)利用代数综合法，可得单元应力的均值和方差为:

式中，μwe，σ2we分别为第e个单元的节点位移均值和方差。

3 算例

以哈勃太空望远镜上的太阳能电池帆板中的悬臂薄壁圆管梁为例，见图3。总长5.91 m，将其划分为50个单元51个节点，则l=0.118 2 m。该结构在t=0 s时刻受到来自太阳的热流S0=1 350 W/m2，假设结构表面初始温度为290 K，σ =5.67 ×10－8W·m－2·K－4，给定Rayleigh阻尼系数α2=β2=0.002，结构其它参数的名义值(均值)见表1［1］。由结构固有频率的计算结果，选取Δt为0.1 s，分析结构的瞬态随机温度场分布及动力响应，并考察各随机参数对响应分散性的影响。

表1 结构各参数的名义值Tab.1 The nominal value of material properties

图4～图9为当随机参数变异系数均为0.01时，结构的温度和动力响应的均值及均方差随时间的历程图。

图4和图5为自由端截面平均温度和截面最大温差均值的时间历程图，从中可见，截面温差的变化率大于平均温度，平均温度在800 s后趋于稳定值400 K，而截面温差在100 s后基本稳定达到10 K。由于温度场的稳态值由初始太阳光入射角、热流密度、散射和吸收系数决定［4－5］，故转角变化导致热流突变，进而产生小幅度变化的截面温差，突变的截面温差又会产生变化的热载荷，从而导致了不稳定的颤振。为了看清截面温差突变效果，给出图5的局部放大图，可见有突变现象存在，但是幅度不大，这是因为结构振动的幅度在初始时段较小，截面转角亦很小，故耦合作用不明显造成的。

图6为自由端横向位移均值的时间历程，可见振动有增强且伴有小幅度的突变，表现为颤振，颤振的幅度由阻尼和光照入射角决定，其中以阻尼为最主要因素，算例选取较小的阻尼系数为了使耦合颤振效果更为明显。另见自由端的准静态位移由0迅速增大并趋于稳定，这是由截面温差的变化规律决定的。

图7为最大应力固定端处应力均值随时间变化历程，可见其变化规律与图4平均温度相似，随着平均温度的升高不断增大，且伴随着由热振动造成的应力扰动，扰动随着颤振而增强，这有可能造成结构的破坏或功能失效，且长期作用亦可能引发结构的热疲劳破坏。

由图8和图9响应的均方差分析结果可见，截面最大温差分散性与随机参数的分散性基本一致，位移响应分散性随着时间的增加逐渐增大且显出振动特性，这是由热－结构耦合作用产生的热颤振引起的。

为了考察各随机参数分散性对响应结果的影响，表2列出了所有随机参数变异系数取不同值时自由端横向位移及固定端应力响应的均值和均方差在100 s时刻的结果。由于E和ρ呈正相关，故两者的变异系数相同。

表2 动力响应在100 s时的均值和均方差Tab.2 The mean value and standard deviation of dynamic responses at the one hundred seconds

从表2中的计算结果可见:参数的随机性对响应分散性(均方差)影响明显，当所有随机参数变异系数均增大10倍时，响应亦以近10倍关系增大。针对各参数随机性对响应均值和均方差影响程度评估上，E和ρ的随机性对位移和应力响应均值均有一定影响。E，ρ和α的随机性对位移和应力响应分散性影响很大。比较其它随机参数，αs，k对位移和应力响应分散性影响较大，ε和c则影响很小。为了验证本文结果的正确性，这里利用Monte-Carlo方法检验。由于MC方法需要大量的抽样模拟，对于本文瞬态随机性问题，计算量巨大，为此，本文对所有随机模型均给出了3 000次MC法的数值模拟结果，对比可见，本文方法的结果与MC法的结果相差不大，但本文方法可直接一次性的得到各时间步处温度场及动力响应的数字特征，具有较高的计算效率。

4 结论

本文对综合考虑热－结构耦合关系和参数具有随机性的空间薄壁圆管梁在瞬态突加热流作用下的动力响应问题进行了研究，理论分析与计算结果表明:

(1)热－结构耦合将有可能导致结构不稳定的热颤振，且使动力响应的幅值增大。

(2)结构参数的随机性对响应分散性影响不可忽略，其中弹性模量E，质量密度ρ，线膨胀系数α，热吸收系数αs和热传导系数k对响应分散性影响较大，而散射系数ε和比热容c则相对较小。

(3)通过与Monte-Carlo数值模拟法的结果对比表明，本文的求解方法可行且有效。

［1］ Ding Y，Xue M，Kim J K.Thermo-structural analysis of space structures using fourier tube elements［J］.Comput Mech，2005，36:289－297.

［2］ Xue M D，Duan J，Xiang Z H.Thermally-induced bendingtorsion coupling vibration of large scale space structures［J］.Comput Mech，2007，40:707－723.

［3］ 程乐锦，薛明德.大型空间结构热－动力学耦合有限元分析［J］.清华大学学报(自然科学版)，2004，44(5):681－684.CHENG Le-jin，XUE Ming-de.Coupled thermal-dynamic FEM analysis of large scale structures［J］.J Tsinghua Univ(Sci＆Tech)，2004，44(5):681－684.

［4］ Ribeiro P，Manoach E.The effect of temperature on the large amplitude vibrations of curved beams［J］.Journal of Sound and Vibration，2005，285:1093－1107.

［5］ Hassan M A，Kanno I，Kotera H.Compound two-dimensional thermo-elastic and thermodynamic analysis for c-axis-oriented epitaxial lead titanate thin films［J］.Vacuum，2006，81:461－467.

［6］ 王勖成，邵 敏.有限单元法基本原理和数值方法［M］.北京:清华大学出版社，1997.

［7］ 王小兵，陈建军，梁震涛，等.热机电耦合随机参数智能板结构的数值求解［J］.西安电子科技大学学报，2008，35(4):592－599.WANG Xiao-bing，CHEN Jian-jun，LIANG Zhen-tao，et al.Randomicity analysis of the piezothermoelasticity intelligent thin plate by appling the numerical method［J］.Journal of Xidian University，2008，35(4):592－599.

［8］ 魏永祥，陈建军，王敏娟.随机参数齿轮－转子系统的扭转振动分析［J］.航空动力学报，2010，25(11):2637－2642.WEIYong-xiang， CHEN Jian-jun， WANG Min-juan.Dynamic response of torsional vibration of gear-rotor with random parameters［J］.Journal of Aerospace Power，2010，25(11):2637－2642.

［9］ Salam M R A E，Alla A M A，Hosham H A.A numerical solution of magneto-thermoelastic problem in nonhomogeneous isotropic cylinder［J］.Applied Mathematical Modelling，2007，31:1662－1670.

［10］ 吴永礼.计算固体力学方法［M］.北京:科学出版社，2005.