亚音速超空泡射弹尾拍动力学响应分析

魏英杰，何乾坤，王 聪，曹 伟，张嘉钟

(哈尔滨工业大学 航天学院，哈尔滨 150001)

航行体在水下高速运动时，航行体表面附近的水因低压而发生相变，产生空化现象。当航行体的运动速度足够高时，空泡将完全包裹航行体形成超空泡［1］。超空泡的存在将使水下航行体的摩擦阻力大幅减小，从而使水下射弹等小尺度水下航行体的速度提高到1 000m/s的量级［2］。当超空泡射弹在水下高速运动时，任何小的扰动，如射弹在发射时的扰动及水下横向扰流等，都会使射弹的尾部与空泡壁面发生连续反弹碰撞，即尾拍现象［3］。

近年来，高速超空泡射弹的尾拍现象引起了国内外学者的广泛关注，并开展了一系列的数值研究工作。目前关于超空泡射弹的研究主要集中于超空泡的流体动力学特性以及超空泡射弹的弹道研究［4］，超空泡射弹结构振动方面的研究不多。Ruzzene［5］基于射弹尾拍运动绕空化器转动的假设，约束了空化器的平动位移，建立了超空泡航行体的尾部与空泡壁上下撞击的力学模型，分析了在冲击力作用下超空泡航行体的结构动力学响应。杨传武［6－7］利用有限元软件分析了超空泡航行体的固有特性，并计算了冲击载荷作用与动态轴向载荷作用下超空泡航行体的结构响应。张劲生［8－9］利用有限元软件计算了超空泡射弹振动应力应变随速度的变化规律。然而，以往的超空泡射弹尾拍文献中确定空泡形态的经验公式均未考虑流体的可压缩性。而实际超空泡射弹在水中运动的速度非常高，因此，水的可压缩性是空泡形态的重要影响因素之一。

本文针对超空泡射弹在运动过程中的尾拍振动问题进行了研究，考虑了水的可压缩性对空泡形态的影响，并基于流固耦合方法，推导了超空泡射弹在无约束条件下的振动方程，利用有限元法对振动方程进行求解，分析了亚音速下结构振动响应随马赫数的变化关系。

1 亚音速可压缩超空泡形态分析

超空泡射弹在水中以高速运动时，水的可压缩性对空泡形态的影响必须予以考虑。超空泡射弹一般具有大长细比的特征，对此类细长形超空泡射弹，可以假定它引起的流场为小扰动，并采用细长体小扰动理论进行研究。

假设无穷远处来流三个方向的速度分量分别为:

密度、压力分别为ρ∞、p∞，相应的音速为c∞，则马赫数

假定将一固体置于此均匀流场中，则物体会对基本流动进行扰动，并改变来流的速度场，受扰动的速度场可表达为:

其中，u，v，w为扰动速度分量。考虑扰动速度与均匀流速度V相比是小量的情况:

对于旋转体，扰流是轴对称的，即所有子午面内的流动情况相同。因此，描述该问题的速度势满足［10］:

图1 Riabushinsky闭合方式示意图Fig.1 The Riabouchinsky scheme for the cavitation flow

如图1所示，假设小角度锥形空化器长l，空化器半径Rn，空泡长度Lc，空泡最大直径Rc，并令 L=2l+Lc。将细长体半径R1(x)及空泡半径R(x)写成以下形式:

式中，ε=Rc/L。该边界条件为:

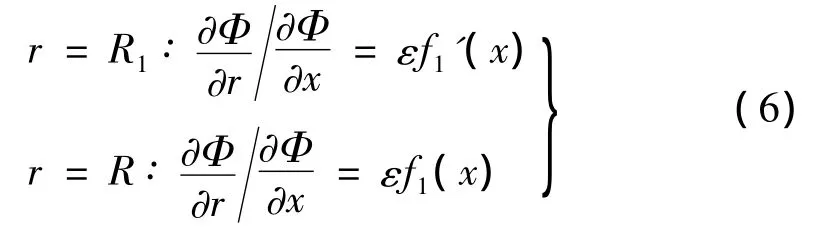
伯努利方程满足:

压强p与密度ρ的关系由Tait方程描述［11］:

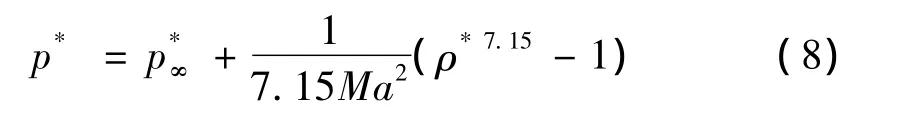
将上式代入式(7)后展开可得动力学边界条件:

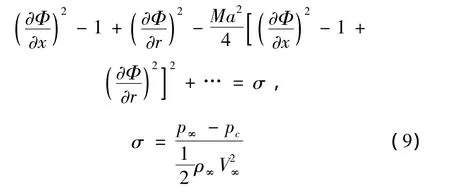
由小扰动理论，可将速度势表达为:

式中，φ为扰动速度u，v，w的扰动速度势，且当r→∞时，φ=0。将式(10)代入式(9)，并略去ε4ln2ε的高阶小量，可得:

对于细长体(如细长锥形射弹及其超空泡)来说，其速度势可用对称轴上连续分布的源汇来代替，满足方程(4)的φ的解的形式可表达为:

式中，q(x)=S'(x)为源强分布密度，S(x)=πr2为细长体横截面面积。

在对称轴附近 φ(x，r)具有以下形式的渐进表达式［12－13］:

假定超空泡采用 Riabushinsky闭合方式，将式(13)代入式(11)可得空泡积分－微分方程:

上式满足边界条件:

取弹体小参数ε1=Rn/l，其中Rn为细长体底部界面半径。对超空泡半径和空化数按小参数ε1作摄动展开［14］:

一阶展开近似解方程为:

方程(17)的解可表示成:

因此，可得空泡半径一阶解为:

若以圆锥空化器底面中心点为原点，则空泡轮廓可表达为:

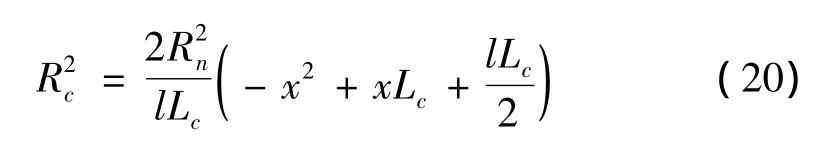
不同马赫数下，流体的可压缩性对超空泡形态的影响有所不同。文中参考高速超空泡射弹相关专利头型［15］，计算了半锥角 22.5°情况下的空泡形态。图 2给出了Ma=0.674 4与Ma=0(不可压缩)情况下的空泡形态对比，可以看出相对于不可压缩流体来说，流体的可压缩性使空泡最大半径及空泡长度都有所增大。图3给出了不同马赫数对空泡形态的影响，可以看出空泡最大截面半径Rk和空泡长度Lc随着马赫数的增大而增大。

图2 不同马赫数下空泡形态(Ma=0.674 4)Fig.2 Cavity profile(Ma=0.674 4)

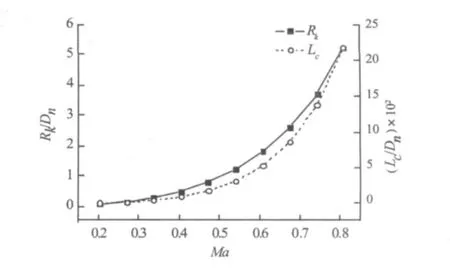
图3 马赫数对空泡形态影响Fig.3 Effect of compressibility on supercavity profile in different Mach numbers

2 超空泡射弹尾拍过程动力学方程建立

超空泡射弹的尾拍运动实际上是一个流固耦合过程，即流体与结构互相作用互相影响。本文将超空泡射弹简化为欧拉－伯努利梁，假设超空泡关于轴线完全对称，不考虑结构振动对空泡形态的影响。将整个流固耦合系统分为流体动力学计算、刚体动力学计算和结构动力学计算三个子系统(如图4)，利用交错迭代法计算，各个系统数据计算实时传递。流体动力学模块主要计算流体动力学载荷;刚体动力学模块主要计算结构做刚体运动时的位移、速度、转角及转动角速度;结构动力学模块主要计算结构做弹性振动时的挠度等。流固耦合作用主要体现在流体载荷和结构弹性振动的挠度耦合。

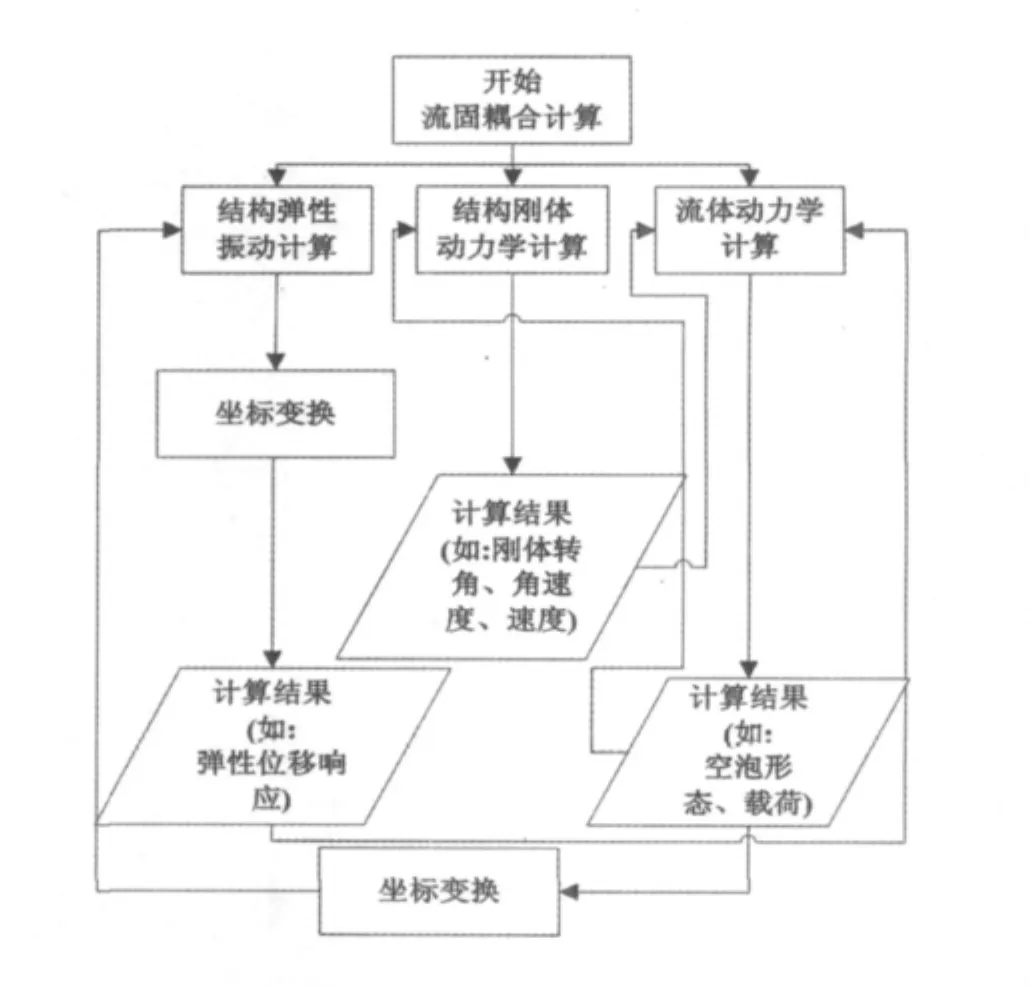
图4 流固耦合迭代流程图Fig.4 Flowchart of FSI simulation

2.1 流体动力学载荷计算

假设射弹在水中以速度V在铅垂平面内运动，超空泡射弹在航行过程中受力包括:空化器受到的阻力FD，尾拍作用的升力RL、阻力RD。

图5 超空泡射弹变形及受力示意图Fig.5 Forces applied to the supercavitating projectile

空化器阻力可表达为:

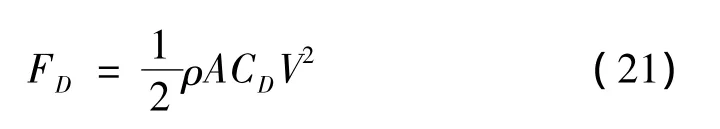
式中，A为空化器截面面积;V为射弹速度;CD为阻力系数［16］。

图6 动量传递示意图Fig.6 Momentum transfer

尾拍作用的升力RL、阻力RD可以根据动量守恒求出。水相对于结构的速度为，假设结构撞水时，在dt时间里使质量为dm来流的动量发生改变，dm=ρA1Vdt。根据牛顿第三定律，水将受到与RL、RD大小相等方向相反的力，我们将其定义为和，在该力的作用下将使水的动量发生改变。不考虑结构的速度在碰撞过程中的速度损失，因此质量为dm的水相对结构的速度大小没有改变，只是方向发生了改变。由图6速度矢量合成图可以发现,改变了边界层水的流向，该部分动量改变量为dmVL,方向与 方向相同使水在来流方向的动量发生了损失，该部分动量改变

量为dm(V－Vt),方向与 方向相反。因此可得:

由:

因此结构发生尾拍时所受阻力和升力可表达为:

式中:θ为弹体轴线和空泡轴线之间的夹角;A1=λδd为射弹尾部浸入液体边界层的特征面积，λ=0.5为经验常数;δ为射弹尾部浸入液体的深度［17］。

图5给出了尾拍浸水深度与结构变形示意图。图中δ为实际浸水深度，δr为不考虑结构变形的浸水深度，q为结构变形。从图中可以观察到，如果不考虑流体与结构之间的相互作用，则δ=δr;若考虑了流体与结构之间的相互作用，则δ=δr－q。

2.2 射弹刚体动力学模型建立

当射弹尾部完成撞击并反弹进入空泡内部，根据动量矩守恒可知，射弹在该阶段的动力学方程可以表达为:

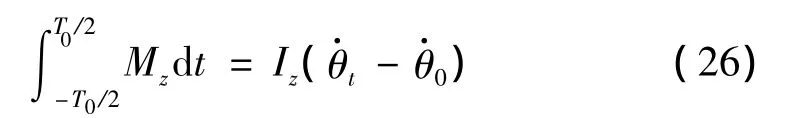
其中:Mz=－RDasinθ－RLacosθ，和分别为撞击前后航行体角速度，Iz为射弹转动惯量，a为尾拍力作用点距质心距离，τ为完成一次尾拍需要的时间。Rand［17］给出了尾拍半周期τ的近似表达式:

2.3 射弹结构动力学模型建立

假设超空泡射弹在平面内发生尾拍运动，由于射弹在水中被超空泡完全包裹，没有固定边界约束作用，射弹的振动方程可写为:

式中:q为射弹的结构位移，［M］、［C］、［K］分别为系统质量、阻尼和刚度，{F}为系统所受外力。当射弹不受外力作用，即{F}=0时，可以求解出系统的固有频率{ω}和主振型{Φ}，文中截取了系统的前17阶模态。由于系统没有固定边界约束，因此系统具有刚体运动，系统的前2阶模态为固有频率等于0的刚体模态，分别对应系统在平面内两个自由度的刚体位移，系统的后15阶模态为弹性振动模态。根据模态叠加法，引入模态坐标{ξ}，对方程(1)实行坐标变换并左乘{Φ}T，得:

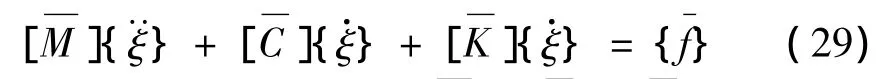
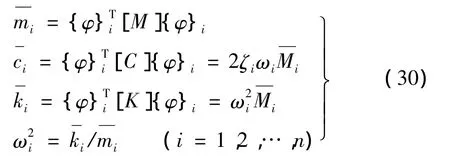
由于系统前两阶固有频率ω1=ω2=0，根据主振型的正交性，系统矩阵可写做:

方程(31)可以分解为:

因此，方程(32)为系统的刚体运动方程，方程(33)为系统的弹性振动方程。

3 可压缩性对超空泡射弹尾拍动力学的响应影响

超空泡射弹在水下以高速运动，水的可压缩性会对超空泡射弹尾拍运动产生影响。基于第1节得出的可压缩超空泡形态，并结合第2节受力分析和动力学方程，计算了流体的可压缩性对超空泡射弹尾拍动力学响应的影响，计算中考虑了流固耦合作用。超空泡射弹尺寸及属性参数见表1。

图7和图8分别给出了流体可压缩性对超空泡射弹刚体转角和尾拍力的影响(Ma=0.534)。由于流体可压缩性使超空泡射弹的空泡轮廓增大，因此射弹刚体转角幅值有所增大，且射弹两次尾拍之间的时间间隔也有所增大;根据公式(27)可知，射弹尾拍半周期τ减小，但由图8可以看出τ的减小量可以忽略，因此流体的可压缩性使结构刚体转动的周期T增大。由于流体可压缩性使射弹刚体转角增大，因此根据公式(24)可知，尾拍升力RL的幅值变大，阻力RD的幅值变小。而且，由于流固耦合作用，使尾拍力变得不光滑。

图9给出了流体可压缩性对超空泡射弹尾部点弹性位移响应的影响(Ma=0.534)。由于流体的可压缩性使尾拍力幅值的变大，因此在该作用力下结构在尾拍期间的弹性位移响应幅值增大，但尾拍结束后，结构在空泡内的振动几乎不受流体可压缩性的影响。

图10 不同马赫数下结构振动最大幅值比较Fig.10 Maximum deflections at different Mach numbers

图10给出了不同马赫数下结构尾部弹性位移响应幅值变化，从图中可以看出:Ma＜0.3时，流体可压缩性对结构尾部弹性位移响应影响很小，因此可以将流体考虑成不可压缩流进行计算;Ma≥0.3时，流体的可压缩性对结构尾部弹性位移响应的影响随马赫数的增大而逐渐增大，尤其是Ma≥0.6时，增大效果更加明显;结合图3还可以看出，流体可压缩性对结构弹性位移的影响与其对空泡形态的影响相吻合。

4 结论

本文通过求解无约束超空泡射弹的耦合动力学方程，对可压缩流体中的射弹尾拍结构振动响应进行了研究，通过分析得到以下几点结论:

(1)流体的可压缩性使超空泡射弹刚体转动的周期和幅值增大;使尾拍升力幅值增大，阻力幅值减小。

(2)流体的可压缩性使结构尾部在尾拍期间的弹性位移响应幅值增大，但尾拍结束后，结构在空泡内的振动几乎不受流体可压缩性的影响。

(3)当Ma＜0.3时，流体可压缩性对结构弹性位移响应影响很小，且该影响随马赫数的增大而逐渐增大，尤其是Ma＞0.6时，增大效果更加明显。

［1］ 吕志民，申 超，陈永奎.超空泡射弹技术探讨［J］.舰船科学技术，2007，29(1):92－94.LÜ Zhi－min，SHEN Chao，CHEN Yong－kui.The research of supercavitation projectile technology［J］.Ship Science and Technology，2007，29(1):92－94.

［2］ Savchenko Y N.Control of supercavitation flow and stability of supercavitating motion of bodies［C］.VKI Special Course on Supercavitating Flows.Brussels:Rto2avt and vki，2001:313－341.

［3］ 孟庆昌，张志宏，顾建农，等.超空泡射弹尾拍分析与计算［J］，爆炸与冲击，2009，29(1):56－60.MENG Qing－chang，ZHANG Zhi－hong，GU Jian－nong，et al.Analysis and calculation for tail－slaps of supercavitating projectiles［J］.Explosion and Shock Waves，2009，29(1):56－60.

［4］ Kulkarni S S，Pratap R.Studies on the dynamics of a supercavitating projectile［J］. Applied Mathematical Modeling，2000，24:113－129.

［5］ Ruzzene M，Soranna F.Impact dynamics of elastic stiffened supercavitating underwater vehicles［J］.Journal of Vibration and Control，2004，10:243－267.

［6］ 杨传武，王安稳.冲击载荷作用下超空泡水下航行体的结构响应［J］.华中科技大学学报(自然科学版)，2008，36(7):129－132.YANG Chuan－wu，WANG An－wen.Structural response of supercavitating underwater vehicles subjected to impact loads［J］.Huazhong Univ.of Sci.＆ Tech.(Natural Science Edition)，2008，36(7):129－132.

［7］ 杨传武，王安稳.动态轴向载荷对超空泡航行体振动特性的影响［J］.华中科技大学学报(自然科学版)，2008，36(12):71－74.YANG Chuan－wu，WANG An－wen.Influence of dynamic axial loads on the vibration characteristics of supercavitation underwater vehicle［J］.Huazhong Univ.of Sci.＆ Tech.(Natural Science Edition)，2008，36(12):71－74.

［8］ 张劲生，张嘉钟，魏英杰，等.超空泡水下航行体的结构动力响应特性［J］.北京航空航天大学学报，2010，36(4):411－414.ZHANG Jin－sheng，ZHANG Jia－zhong，WEI Ying－jie，et al.Structural dynamic response characteristics of supercavitating underwater vehicles［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36(4):411－414.

［9］ Zhang J Z，Zhang J S，Wei Y J.Simulation of tail－slap loads ofsupercavitating projectiles［C］. Third International Conference on Information and Computing，Jiangnan:IEEE，2010:163－166.

［10］ Vasin A D.Supercavities in compressible fluid［Z］.VKI/RTO Lecture Series on Supercavitating Flows，Von Karman Institute for Fluid Dynamics.Brussels，Belgium，2001.

［11］ Zamyshlyaev B V， YakovlevY S. Dynamicloadsin underwater explosions［M］.Sudostroenie，Leningrad，1967.

［12］ Frankl F I，Karpovich E A.Gas dynamics of slender bodies［M］.Gostekhizdat，Moscow，1948.

［13］ Ashley H，Landahl M T.Aerodynamics of wings and bodies［M］.Addison Wesley，Massachusetts，1965.

［14］ Serebryakov V V. Some models of prediction of supercavitation flows based on slender body approximation［C］.Cav2001:session B3.001:1－13.

［15］ Castano J M，Kuklinski R.High－speed supercavitating underwater vehicle［P］.United States:US 6739266 B，2004－05－25.

［16］ May A.Water entry and the cavity－running behavior of missiles［R］.Maryland:NTIS，1975.

［17］ Rand R，Pratap R，Ramani D，et al.Impact dynamics of a supercavitating underwater projectile［C］.Proceedings of DETC'97.California:ASME，1997:1－11.

［18］ Mukhopadhyay M.Vibrations dynamics and structural systems(2nd ed)［M］.Rotterdam:A.A.Balkema Publishers，2000.246－247.