对量子力学中态叠加原理的探讨

丁汉芹，刘伟霞，张 军

（新疆大学物理科学与技术学院，新疆乌鲁木齐830046）

对量子力学中态叠加原理的探讨

丁汉芹，刘伟霞，张 军

（新疆大学物理科学与技术学院，新疆乌鲁木齐830046）

阐述了量子力学中态叠加原理的重要性，分析了教材中该原理的几种不同的表述，并强调了波函数的相因子对叠加态的重要影响。

量子力学；态叠加原理；波函数；探讨

量子力学是研究微观量子系统运动变化规律的理论，它是在上个世纪20年代在总结了大量实验事实和旧量子论的基础上建立起来的。目前，量子力学已形成了相当完整的、系统的理论，它的全部内容可以从少数几个基本原理出发，通过严格逻辑推理的方法推演出来。不同的著作对量子力学基本原理的表述方法不尽完全相同，原理的数目和每条原理的内容也不完全一样，但从整体上来看，其总的内涵没有多大的区别，这些基本原理以及由此推出的全部内容早已为物理学界所公认。尽管如此，但对某些基本原理的描述，以及对微观世界物理图像的看法还是存在着一定的分歧，尤其是对量子态叠加原理的认识更是仁者见仁、智者见智。为此，本文拟对这个问题作初步探讨。

1 几种典型的表述

在量子力学理论中，态叠加原理起着统制全局的作用，被称之为“量子力学中头等重要的原理”[1]。不同的学者对这个原理给出了不同的表述，我们选择国内教材中4种典型的说法作以探讨。

（1）周世勋的表述[2]：对于一般的情况，如果Ψ1和Ψ2是体系的可能状态，那么它们的线性叠加Ψ＝c1Ψ1+c2Ψ2（c1，c2是复数）也是体系的一个可能状态。当粒子处于态Ψ1和态Ψ2的线性叠加态Ψ时，粒子是既处在态Ψ1，又处在态Ψ2。

（2）钱伯初的表述[3]：物理体系的任何一种状态（波函数Ψ）总可以认为由某些其他状态（波函数Ψ1，Ψ2，…）线性叠加而成，即Ψ＝C1Ψ1+C2Ψ2+…，（C1，C2，…为复常数）。如果Ψ1，Ψ2，…是可以实现的状态（波函数），则它们的任何线性叠加态Ψ总是表示一种可以实现的状态（波函数）。当物理体系处于这种叠加态Ψ时，可以认为该体系部分地处于Ψ1态，部分地处于Ψ2态，等等。

（3）曾谨言的表述[4]：设体系处于Ψ1描述的态下，测量力学量A所得结果是一个确切值a1（Ψ1称为A的本征态，A的本征值为a1）。又假设在Ψ2态下，测得的结果是另一个确切值a2，则在Ψ＝c1Ψ1+c2Ψ2所描述的状态，测量所得的结果，既可能为a1，也可能为a2（但不会是另外的值），而测得结果为a1或a2的相对几率是完全确定的。我们称Ψ态是Ψ1态和Ψ2态的线性叠加态，而且量子力学中态叠加原理是与测量密切联系在一起的。

（4）喀兴林的表述[5]：若Ψ1和Ψ2是体系的两个可能的状态，则Ψ＝c1Ψ1+c2Ψ2也是粒子可能的状态。叠加态Ψ既不是Ψ1态，也不是Ψ2态，它是一个新态。

2 分析与讨论

以上几种表述虽有所不同，但一致的观点是：若Ψ1和Ψ2是体系的两个可能的态，则它们的线性叠加态Ψ＝c1Ψ1+c2Ψ2也是体系可能的状态，这种叠加并且可以推广到很多态。这来源于以下几个方面共同的认识：第一，在量子力学中，波函数被用来描述一个物理体系的状态，它的模方|Ψ|2表示在空间找到该粒子的几率密度（假定波函数已归一化），而波函数本身并没有直接的物理意义，即Ψ本身不是可观察的物理量。第二，量子力学中的基本方程是薛定谔方程，波函数Ψ1，Ψ2，…，以及它们的线性叠加Ψ都是同一个薛定谔方程的解。第三，量子态的叠加与经典物理中叠加原理有着本质的不同。它们都揭示了微观粒子波粒二象性的特征，微观粒子的波函数是可以叠加的，并发生干涉现象，如电子的双缝衍射实验。这是微观世界中最重要的性质，是量子力学的核心内容。但是，我们认为原理中关于叠加态的陈述不是普遍成立的。我们对此作以分析与讨论。

其中，哈密顿量H和波函数Ψ211，Ψ21-1分别为

描述它们叠加态的波函数记作（已归一化）

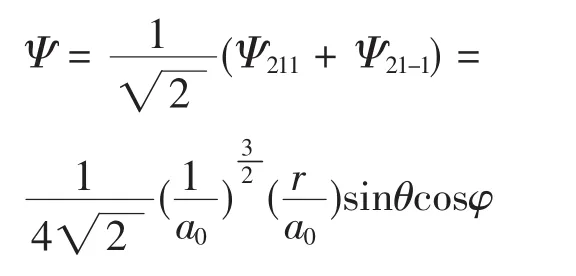
Ψ同样满足上面的薛定谔方程。我们发现，叠加态Ψ描述的是氢原子体系的2PX轨道波函数，它的电子云呈哑铃型的空间对称分布。但是，Ψ211和Ψ21-1描述的电子云都是呈轮胎形状的空间分布量子态。由此可见，叠加态Ψ是一个既不同于Ψ211，又不同Ψ21-1的新量子态。因此，我们没有理由说“粒子既处在态Ψ211，又处在态Ψ21-1”（第（1）种表述），“体系部分地处于Ψ211态，部分地处于Ψ21-1态”（第（2）种表述）。

如此看来，似乎最后一种关于态叠加原理的表述是正确的，即叠加态完全是个不同于Ψ1，Ψ2的新态。但是，实际情况有时未必都是这样，看个例子我们就知道了。设有一个波函数Φ，它是一个不带相因子的实数形式。那么我们知道，Φ和2Φ描述的是同一个态。现在令Ψ1＝Φ，Ψ2＝2Φ，再让这两个量子态叠加Ψ＝C1Ψ1+C2Ψ2。 只要组合系数C1，C2都是实数，且C1≠-2C2，我们得到的还是原来的态，而不是新态。此时，我们不能像第（4）那样说，“叠加态Ψ既不是Ψ1态，又不是Ψ2态，它是一个新态”。

3 总结

我们求得叠加态所描述量子态中粒子的几率密度为

从这个表达式中，我们容易发现，只要相因子中的x≠π，Ψ和Φ描述的量子态中粒子在空间中的相对几率密度是相等的；如果x＝π，则|Ψ|2＝0，但|Φ|2＝0。显然，叠加态Ψ和Φ描述的粒子在空间中粒子的几率分布不一样了。由此可见，描述量子态波函数的相位对形成的叠加态的特征有着非常大的影响。

总之，在表述量子力学中的态叠加原理时，我们认为只要保留四种陈述中的前一部分内容就足够了，即“如果Ψ1和Ψ2是体系的可能状态，那么它们的线性叠加Ψ＝c1Ψ1+c2Ψ2（c1，c2是复数）也是体系的一个可能状态”。没有必要使用令人费解的言语来做不适当的解释，给对该原理的理解和教学带来不必要的困难。如果要强调叠加态的性质，一定要对波函数的相因子做相应的考虑和分析，从而保证陈述的科学性和准确性。

[1]Landu LD，Lifshitz EM.Quantum mechanics，non-relativistic theory[M].Oxford：Pergamon Press，1977：7.

[2]周世勋.量子力学教程[M].北京：高等教育出版社，1979：22-23.

[3]钱伯初.量子力学[M].北京：高等教育出版社，2006：70-71.

[4]曾谨言.量子力学导论[M].北京：北京大学出版社，1998：33-34.

[5]喀兴林.高等量子力学[M].北京：高等教育出版社，2000：65-67.

〔责任编辑 李海〕

Discussions on the S uperposition P rincip le of S tates in Q uantum M echanics

DING Han-qin，LIUWei-xia，ZHANG Jun
（School of Physical Science and Technology，Xinjiang University，Urumqi Xinjiang，830046）

The significance of the superposition principle of states in quantum mechanics is presented，and various statements of this principle in a few textbooks are commented.The important effect of phase factor in wave function on superposed state is emphasized.

quantum mechanics；the superposition principle of states；wave function；discussion

O 413

A

1674-0874（2012）04-0022-02

2012-05-05

新疆维吾尔自治区自然科学基金资助项目[2012211A012]；新疆大学博士启动基金资助项目[BS110105]

丁汉芹（1969-），男，安徽安庆人，博士，讲师，研究方向：凝聚态物理。