基于双线阵CCD的交汇测量模型及布站方式研究

韩丙辰，曹 姣，郝雯霞，吕仕儒，杨成全

（山西大同大学物理与电子科学学院，山西大同037009）

基于双线阵CCD的交汇测量模型及布站方式研究

韩丙辰，曹 姣*，郝雯霞，吕仕儒，杨成全

（山西大同大学物理与电子科学学院，山西大同037009）

针对靶场测量中立靶密集度参数的测量需求，基于交汇测量原理，对双线阵CCD交汇测量的模型进行了分析。详细推导了交汇测量时计算坐标的数学模型，并针对不同数学模型进行了讨论。由于双线阵CCD交汇测量模型不需要在有效定位范围内布置多个传感器，系统复杂程度和成本均与需要定位的面积无关，因此在大型定位系统中占有优势。

光幕靶；交汇测量；线阵CCD

CCD光幕靶交汇测量技术是基于光电检测技术的一种非接触式二维光电测量技术[1-8]，它对测试条件的要求比较简单，无须人工背景，对测试弹丸也无特殊要求，可以实现较远距离的自动测试，并且可以根据弹丸直径来设置有效靶面，因此交汇测量系统具有测量精度高、布站简单、自动化程度高等优点，基本上可以满足大部分口径常规武器的立靶精度测试要求。目前，基于交汇测量原理的双线阵CCD布站方式已在大型动态目标的轨迹测量上得到了诸多的应用。本文中根据双线阵CCD交汇测量的原理，拟对其实现数学模型进行详细的讨论。

1双线阵CCD交汇测量原理

根据几何光学的成像原理，物与像之间必须满足一定的几何关系。基于光学成像原理的特点，通过获取物体所成像的尺寸和位置，就可以推导出物体在物方空间上的位置和几何尺寸，这是许多光学尺寸测量，位置判定仪器的通用工作原理。在对成像尺寸的测量和位置判定时光电检测器件来实现，可以提高成像系统的准确性，再结合计算机技术则可实现测量系统的自动化。

针对空间一点的二维坐标，通常根据人眼视觉原理，把两个线性CCD阵列放置在同一个竖直平面内，且两个的主光轴在竖直平面内交汇于一点，对于两个线性CCD阵列而言构成一个竖直的共视测量靶面。针对两个线性CCD阵列视场在靶面内的交迭区内的任意一点，在各自线阵CCD上均会有一个成像点与之相对应。因此，竖直光电靶面内任意一点的坐标则可通过在CCD上的成像高度结合测量模型计算出来，如图1所示。

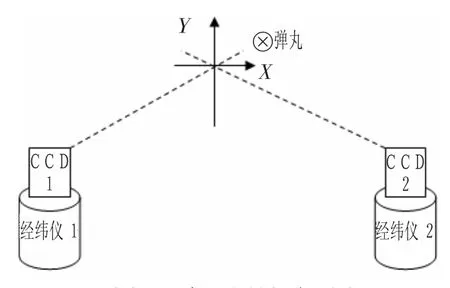
图1 交汇测量原理图

基于上面的原理，通过对两个线阵CCD阵列进行布站，可在竖直空间上构成一个光电检测靶面，通过这一靶面的任何目标都会同时在两个线阵CCD上成像，通过图像采集卡将采集到的图像信号转换为数字信号，再根据两个线阵CCD的高度及线阵CCD之间的距离，结合计算机技术获得靶面目标的精确位置。在利用几何和光学原理进行计算时，可以选择不同的坐标原点来建立坐标系进行坐标计算，为了能够精确获得物体在光幕靶上的坐标信息，且减小测量误差，我们必须针对其布站情况建立合理而有效的坐标系。在此主要有3种坐标系的建立方式：

（1）以两个线阵CCD阵列的光轴交汇点为坐标原点建立坐标系；

（2）以其中一个CCD阵列的中点为坐标原点建立坐标系；

（3）以两个线阵CCD阵列的基线中点为坐标原点建立坐标系[9-13]。

2 双线阵CCD交汇测量模型分析

对于交汇测量原理的数学模型建立，按照3种情况进行分析。①如图2（a）所示，光轴x平行于基线 S1S2；②如图2（b）所示，光轴x与基线S1S2重合；③如图2（c）所示，光轴x与基线S1S2重合。CCD1的中心位于点S1，CCD2的中心位于点S2，|S1S2|＝d0为基线长度。OS1与x轴的夹角为α0，OS2与x轴的夹角为β0（它们被称为是交汇仰角，一般情况下两个CCD交汇时有α0＝β0）。靶面上任意一点M相对于两个线阵CCD的主光线分别为MA，MB，且分别与基线S1S2交于点A，B。点M在两个CCD上成像的像高分别为h1，h2，且h1在光轴OS1之上为正，在OS1之下为负（h2同理，因而图2中所示的h1为正，h2为负）。MA与x轴的夹角为α，MB与x轴的夹角为β。MA与光轴OS1的夹角为γ1，MB与光轴OS2的夹角为γ2，CCD镜头的焦距为f。

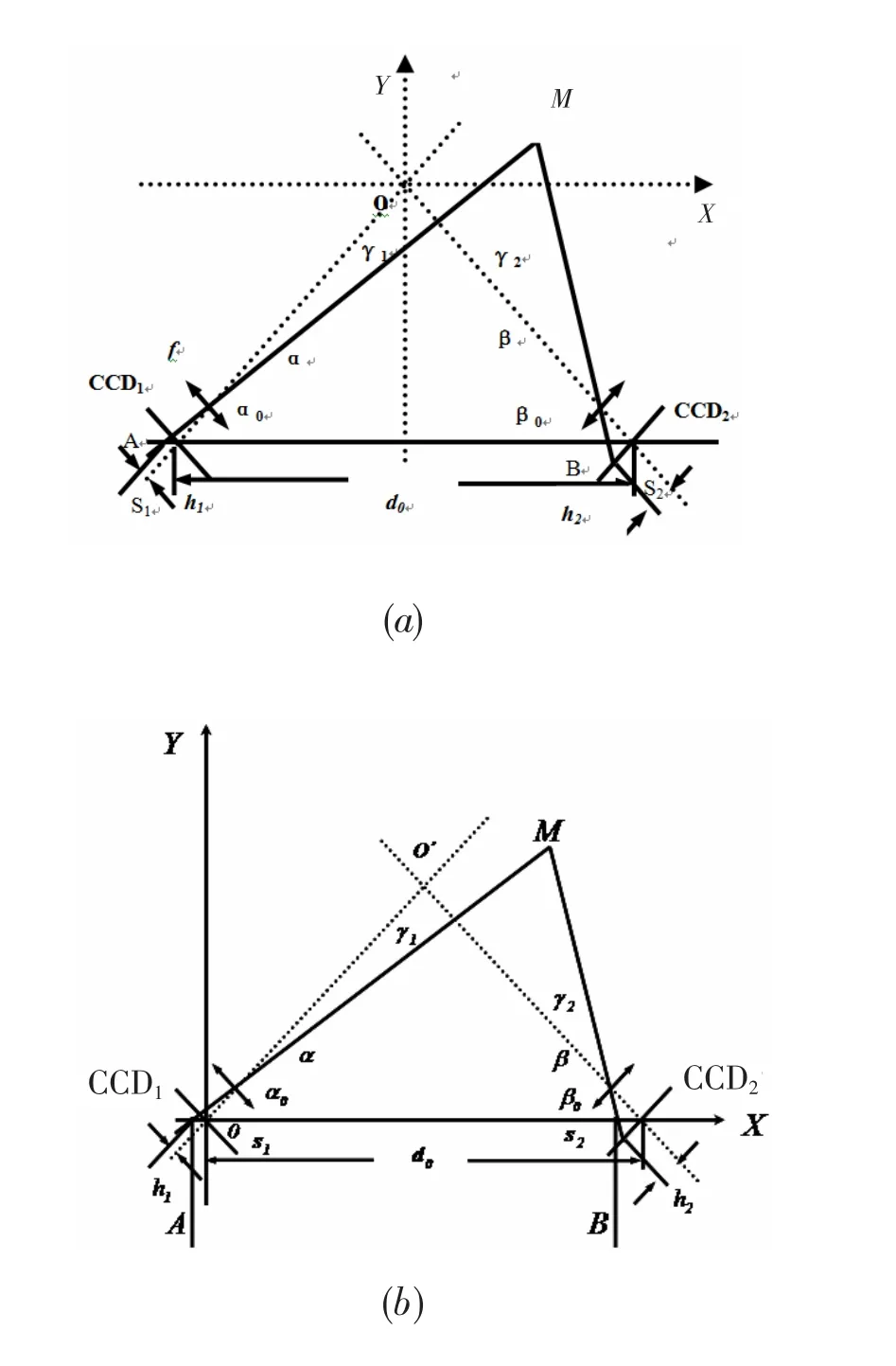
图2 交汇测量模型示意图

由图2（a）可知，其坐标计算公式为：

结合上式以及图2（a）中的几何关系可得到靶面上任意一点M的二维坐标为：

结合上式以及图2（b）中的几何关系，可得到靶面上任意一点M的二维坐标为：

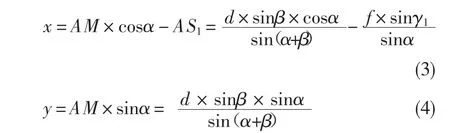
由图2（c）可，知其坐标计算公式为：

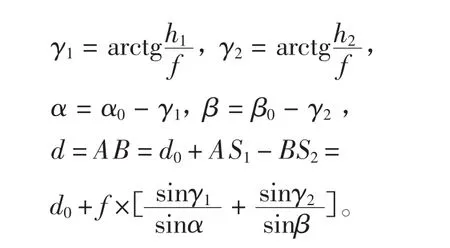
结合上式以及图2（c）中的几何关系可推导出，靶面上任意一点M的二维坐标为：

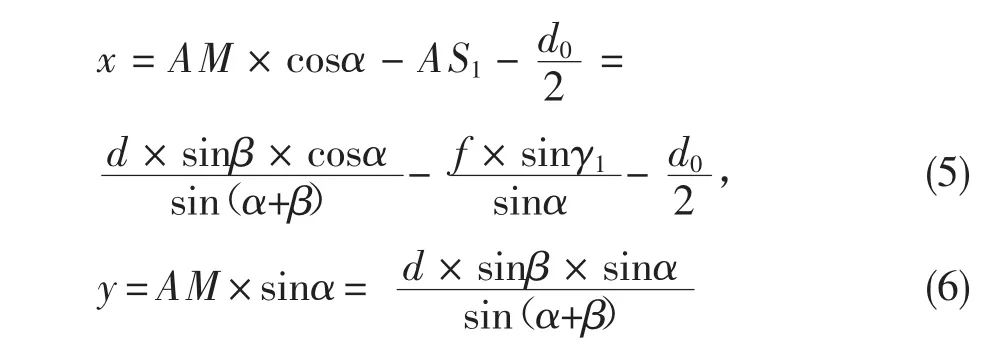
根据交汇测量原理，在推导靶面坐标计算公式时，基本可以建立以上三种数学模型，如果只从靶面位置（即坐标）的判定来考虑，则第一种数学模型比较直观，符合通常人们的视觉习惯，在参阅的文献资料中应用也比较多。但是就立靶精度测量而言，我们所要得到的最终结果是密集度，以上3种数学模型在中间过程得到的坐标数值从理论上来说对于密集度计算没有影响，可以采用3种数学模型中的任意一种进行计算。

前面介绍的第一种数学模型的优点是，得到的坐标表达式非常直观，从而在交汇平面中的坐标分布可以根据实际情况分别得到每个坐标区间的坐标值。基于第一种交汇模型进行布站，在陈树越教授的指导下我们进行了系统实验，由于当时的保密要求，未进行论文的公开发表，现该实验数据已被发表，见文献[1]。但是通过3种模型的计算公式的对比可知，第二种和第三种交汇测量模型的计算表达式相比第一种交汇测量模型更为简单。采用这两种坐标表达式的数学模型在计算时会进一步减小布站时交汇仰角给试验结果带来的误差，而其中又以第二种交汇测量的模型最为简单，不受测量布站时交汇仰角和基线长度的影响，且从（3）和（4）式可知，计算结果都分布在第一象限。然而在实际进行交汇测量时究竟要采用哪种模型，要根据测试系统的需求来确定。

对于靶场的弹丸测试，基于两个线阵CCD的交汇测量构成的大尺度光幕靶，具有结构简单，测量精度高，构成靶面尺寸可任意设定等特点，因此在大尺寸靶面测量具有很大的优势。

3 双线阵CCD交汇测量模型应用探讨

通过对前面交汇测量模型的分析可知，其交汇区域为大尺度时具有一定的优势，因此关于交汇测量大部分的研究集中在靶场测试方面。在双线阵CCD构成的大尺度测量中，若测量的范围主要在中心交汇测量区域进行测量，则具有较高的精确度，而对于离交汇中心较远的共视区域，其测量精确度会明细下降。另外，交汇测量的精确度还依赖于CCD阵列的敏感单元数量和前面的镜头视场角。如果从交汇测量原理考虑，其也用于诸如测量仪器、计算机、电视等显示屏的控制方面，作为一种新型光电触摸屏使用。对于小尺度的交汇测量应用，仅仅依靠两个线阵CCD来记录显示屏区域内的坐标点，则显得其测量精度不够高，因此可以增加线阵CCD阵列数量的方式来获得更高的测量精度，从而实现小尺度的交汇测量任务，从而使交汇测量方法获得更多领域的应用。

4 结束语

通过分析双线阵CCD的交汇测量原理，详细推导了三种交汇测量时计算坐标的数学模型，且对几种数学模型进行了比较，为测量原理的工程化提供了依据。然而基于以上的几种模型构成具体的测量系统时，还要考虑两个CCD布站方式对测量精度的影响，针对不同的应用领域合理地对测量区域进行布站。

[1]王英，曾光宇.双线阵CCD交汇测量立靶精度系统研究[J].光电工程，2011，38（10）：33-38.

[2]靳田保，郝晓剑，周汉昌.双CCD交汇测量高速弹丸落点坐标设计研究[J].电子测试，2011（6）：54-56.

[3]汪大宝，刘上乾，王会峰.双线阵CCD交汇测量系统结构优化与精度分析[J].光学技术，2008，34（增刊）：29-31.

[4]韩丙辰，陈树越.基于数字CCD相机的高速图像采集系统[J].电脑开发与应用，2005，18（5）：40-42.

[5]朱效明，高稚允.双CCD立体视觉系统的理论研究[J].光学技术，2003，29（3）：298-300.

[6]颜树华，吕海宝，杨华勇.TDICCD交汇测量系统同步控制的建模及仿真研究[J].光学技术，2000，26（5）：418-421.

[7]刘文，苏秀琴，王飞.CCD测量系统实现及其实时性讨论[J].光子学报，2002，31（6）：774-777.

[8]钟堰利，贾福娟，丁凌.双CCD交汇测量系统的设计方法[J].光学技术，2002，28（6）：481-484.

[9]杨华勇，吕海宝.双CCD交汇测量系统结构参数的优化设计[J].光学技术，2001，27（4）：348-350.

[10]吴宁.双CCD交汇测量系统结构参数的优化方法[J].电气电子教学学报，2003，25（4）：32-35.

[11]韩丙辰，张清泉，陈树越.线阵CCD交汇测量模型研究与应用[J].科技情报开发与经济，2005，15（5）：188-190.

[12]颜树华，叶湘滨，王跃科.CCD光靶交汇测量精度的理论研究[J].光电子·激光，1999，10（9）：328-332.

[13]吕海宝，杨华勇，谌廷政，等.CCD交汇测量系统优化设计的建模与仿真[J].光学技术，1998（6）：10-12.

[14]李开端，张青臣，赵育良.提高线阵CCD大尺寸自动测量系统精度研究[J].计算机测量与控制，2002，10（1）：21-22.

〔责任编辑 李海〕

Research of I ntersection M easuring M odel based on D ual L ine A array CCD

HAN Bing-chen，CAO Jiao，HAOWen-xia，L U¨Shi-ru，Y ANG Cheng-quan
（School of Physics and Electronic Science，ShanxiDatong University，Datong Shanxi，037009）

According to vertical target intensity parametermeasurement requirements，the line array CCD intersectionmeasuring model is analyzed based on intersection measurement principle，and the mathematicalmodel of the intersection ofmeasurement for calculating the coordinates is derived in detail，and different mathematical models were discussed.Line array CCD intersection measurementmodel does not requiremultiple sensors arranged in the effective positioning，System complexity and costwith the need to locate the area has nothing to do，within the system complexity and cost has nothing to do with the need to locate the area，therefore take advantage of the large-scale positioning system.

screen target；intersectionmeasuring；line array CCD

TN915

A

1674-0874（2012）04-0014-04

2012-05-10

山西省青年科技研究基金[2011021018]；山西省普高创新性实验项目[2010]；山西大同大学博士启动基金[2010B03]

韩丙辰（1976-），男，山西侯马人，博士，副教授，研究方向：光纤通信和光电检测技术；*曹娇，山西省普通高等学校创新性实验项目负责人。