一类离散时间非线性网络控制系统的跟踪性能分析
姜 丽,池小波
(忻州师范学院数学系,山西忻州 034000)
一类离散时间非线性网络控制系统的跟踪性能分析
姜 丽,池小波
(忻州师范学院数学系,山西忻州 034000)
研究了一类非线性离散时间网络控制系统的跟踪性能分析问题,其中,非线性系统用离散Takagi-Sugeno(T-S)模糊模型近似。考虑到网络传播的随机性,数据包丢失建模为Bernoulli分布的序列。因此,跟踪控制系统转化为带有随机参数的模型。基于平行分布补偿性(PDC)技术和随机稳定性理论,对跟踪性能分析提出新准则,且保证在修正意义下,非线性系统输出跟踪线性系统输出。
网络控制系统;T-S模糊模型;跟踪系统;数据包丢失
1 模型与问题描述
本文中,非线性NCSs中H∞输出跟踪控制系统称为非线性网络跟踪控制系统(非线性NTCSs)。考虑如下非线性离散系统

其中,x(k)∈¡n状态向量,u(k)∈¡m是输入向量,y(k)∈¡p是输出向量。x(0)是初始状态,ω(k)∈¡q是干扰输入或模型误差,属于l2[0,∞)。f(x),gi(x),hi(x)(i=1,2)都是与x(k)有关的未知非线性函数。系统(1)由如下离散T-S模糊模型表示:

其中,ξ1(k),ξ2(k),…,ξs-1(k)和ξs(k)均为前件变量,而且ξ(k)=[ξ1(k),ξ2(k),…,ξs(k)]T∈R5是关于x(k)已知常值函数。r是IF-THEN规则数。Mij(i=1,2,…,r,j=1,2,…,s)是模糊集,Ai,Bi,Biω,Ci,Di,Diω(i=1,2,…,r),都是带有适当维数的已知常值矩阵。非线性离散系统为:


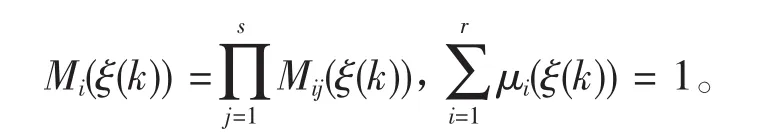
研究问题是设计模糊控制器,使得非线性跟踪系统(1)的输出尽可能的逼近线性跟踪系统输出。
假设跟踪系统为:

其中,xr(k)∈Rnr和yr(k)∈Rp分别是状态向量和输出向量,xr(0)是初始状态,xr(k)∈Rqr是参考输入向量,属于l2[0,∞)。Ar,Br和Cr都是带有适当维数的已知常值矩阵,且Ar是Schur矩阵。
利用PDC技术,模糊控制器与模型(2)具有相同的前件部分。模糊控制器第i条(i=1,…,r)规则为:
Java是一门面向对象编程语言,不仅吸收了C++语言的各种优点,还摒弃了C++里难以理解的多继承、指针等概念,因此Java语言具有功能强大和简单易用两个特征。Java语言作为静态面向对象编程语言的代表,极好地实现了面向对象理论,允许程序员以优雅的思维方式进行复杂的编程。

其中,x¯(k)和 x¯r(k)是控制器输入。K1i∈Rm×n和K2i∈Rm×nr(i=1,2,…,r)是设计的反馈增益。则全局模糊控制器为:

由于网络传播的随机性,数据包丢失可能发生在通信网络。数据包丢失描述为如下Bernoulli分布序列:

其中,λk,δk∈{0,1}是Bernoulli序列,分别表示非线性系统(1)到模糊控制器(5)和跟踪系统(4)到模糊控制器(5)的数据包的丢失现象。 λk,δk,x(k),xr(k)以及ω(k)之间是相互独立的。Bernoulli序列的概率分布为:

其中,已知的常数λ和δ分别表示非线性系统状态和跟踪系统状态的数据包成功到达的概率。
根据以上分析,由(3)、(4)、(6)和(7),得到以下针对闭环非线性NTCS带有随机参数的模型:
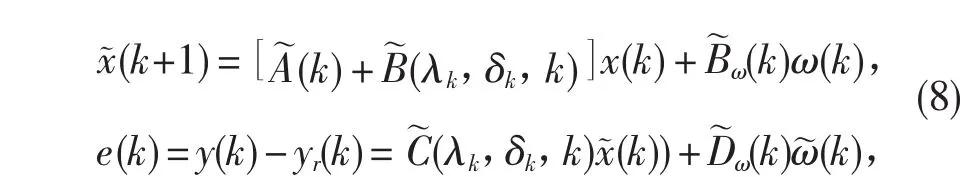


定义1当ω˜(k)=0时,存在常数α>0和τ∈(0,1)使得:成立,则称闭环非线性NTCS(8)是均方指数稳定。
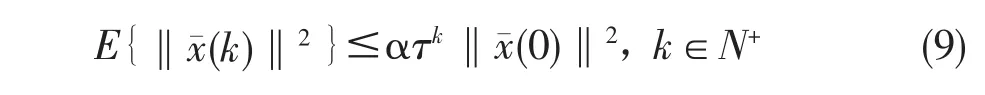

对于所有的非零ω˜(k)∈l2[0,∞),其中,α和γ是常数,M(>0)为权重矩阵。
2 稳定性分析和控制器设计
这节给出修正H∞输出跟踪性能准则。
由相互独立的Bernoulli序列λk和δk,得到:



定理1对于给定的控制器增益矩阵Kij(l=1,2,j=1,2,…,r),权重矩阵M>0,R>0和正标量α,γ,λ以及δ,
如果存在矩阵P>0,Q>0,S>0,T>0,满足
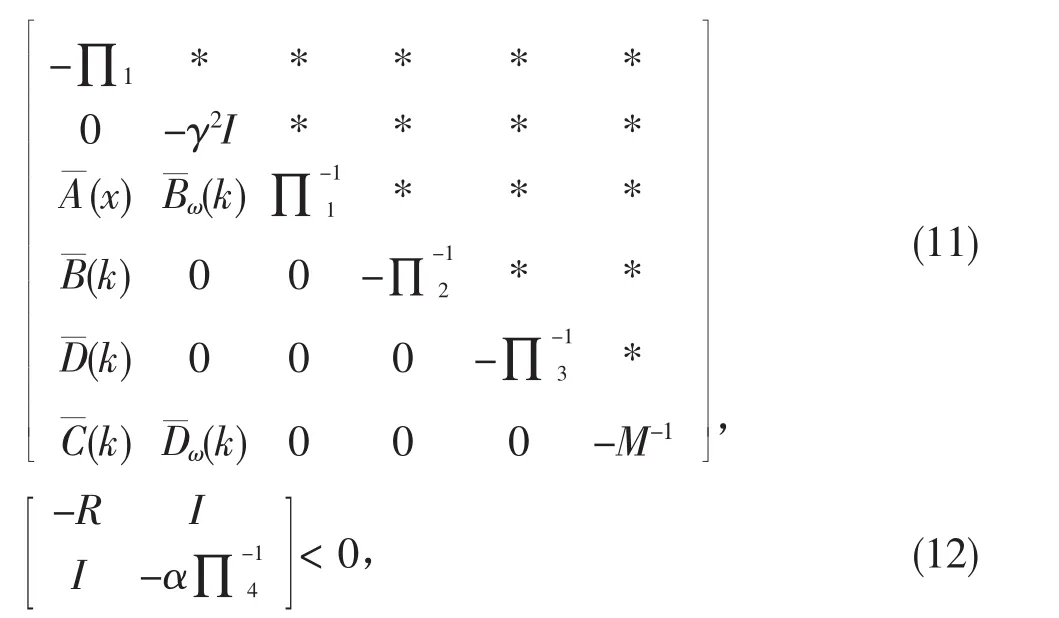
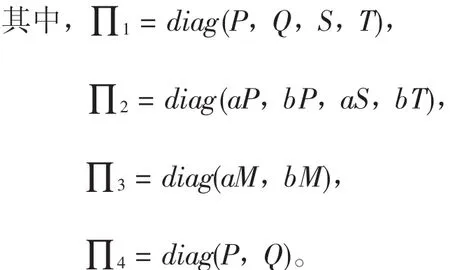

则闭环非线性NTCS(8)达到带有满足(7)式α和γ的修正H∞输出跟踪性能。
证明选取Lyapunov函数为
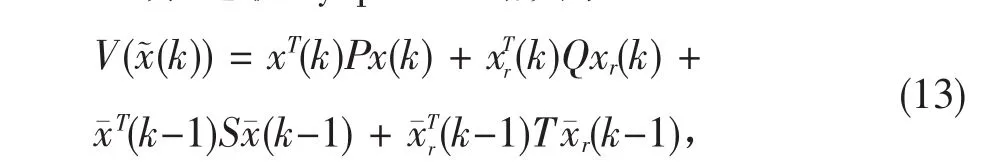
沿着(7)式系统的解,取V(x¯(k))的前向差分,有:
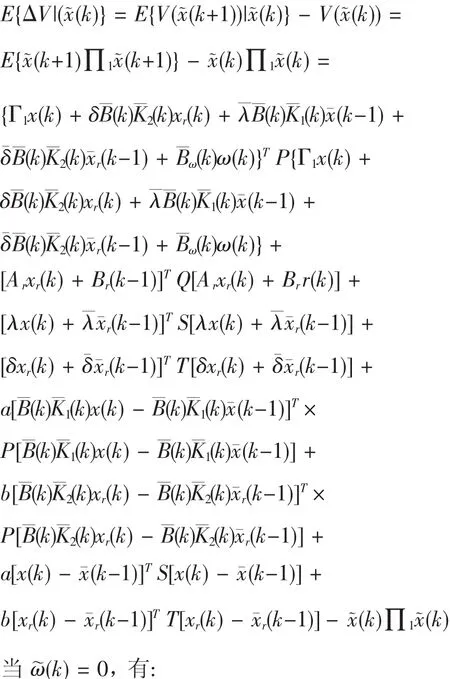
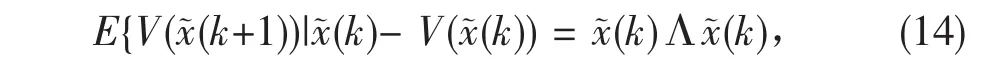
利用Schur补引理,由(11)式得到Λ<0,再根据(14)得到:
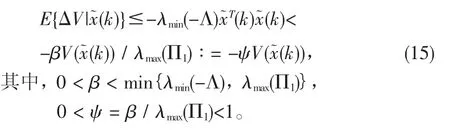
因此,由定义1和定理1得到对于闭环非线性NTCS(8)是均方指数稳定。


根据Schur补引理,由(11)式得到矩阵不等式(16)。因此,

当初始状态xˆ(0)∈Ω={xˆ∶E{xˆTRxˆ}<1},由(12)和(17)得到:

保证了带有α和γ的修正H∞输出跟踪性能。
[1]Hespanha JP,Naghshtabrizi P,Xu Y G.A survey of recent results in networked control systems[J].Proc IEEE,2007,95(1):138-162.
[2]Jiang X F,Han Q L.On designing fuzzy controllers for a class of nonlinear networked control systems[J].IEEE Trans.Fuzzy Syst,2008,16(4):1050-1060.
[3]ZhangW A,Yu L.Output feedback stabilization ofnetworked control systemswith packetdropouts[J].IEEE Trans Autom Control,2007,52(9):1705-1710.
[4]Wang ZD,Yang FW,DanielW C Ho,et al.Robust control for networked systemswith random packet losses[J].IEEE Trans SystMan Cybern B,Cybern,2007,37(4):916-924.
[5]Tseng C S.Model reference output feedback fuzzy tracking control design for nonlinear discrete-time systems with time-delay[J].IEEE Trans.Fuzzy Syst,2006,14(1):58-70.
[6]Jia X C,Zhang D W,Hao X H,et al.Fuzzy tracking control for nonlinear networked control systems in T-S fuzzy model[J].IEEE Trans.Syst.Man Cybern.B,Cybern,2009,39(4):1073-1079.
〔责任编辑 高海〕
Tracking Performance Analysis for Nonlinear Discrete-Time Networked Control Systems
JIANG Li,CHIXiao-bo
(DeparementofMathematics,Xinzhou Teachers College,Xinzhou Shanxi,034000)
This paper is concerned with the tracking performance analysis problem for a class of nonlinear discrete-time networked control systems,where the nonlinear plant is approximated by a discrete-time Takagi-Sugeno (T-S)fuzzy model.Considering the random characteristics of network transmission,data packet dropout ismodeled as a Bernoulli sequence.Then,a new model with stochastic parameters is established for such tracking control system.Based on parallel distributed compensation(PDC)scheme and stochastic stability theory,a new criterion is proposed for such tracking performance analysis,which guarantees that the output of the nonlinear plant tracks thatof a tracked plant in themodified sense.
networked control systems;T-S fuzzymodel;tracking control;data packet dropout
TP13
A
1674-0874(2012)04-0011-03
2012-05-25
姜丽(1981-),女,山西忻州人,硕士,助教,研究方向:模式识别与智能系统。

