矩阵变换器空间矢量调制策略的简化算法

王汝田，马瑞枫，张卓琳，李 海

(1.东北电力大学 电气工程学院，吉林 吉林 132012;2.元宝山发电有限责任公司，内蒙古 赤峰 027000;3.中油吉林石化公司合成厂，吉林 吉林 132021;4.丰满发电厂，吉林 吉林 132001)

矩阵变换器以其优良的输入输出性能，以及能量双向传递，无中间储能元件，结构紧凑，输出频率不受输入频率限制，输入功率因数可调等优点，成为近年来研究的一个热点[1－5]。但是其控制策略复杂，计算量大，而且需要复杂的换流控制电路，降低了系统的可靠性，限制了矩阵变换器在实际中的应用，所以目前矩阵变换器仍然停留在实验室研究阶段，还不能步入工业应用。

空间矢量调制(SVPWM)策略是一种优秀的调制方法，也是最有可能率先在实际中应用的调制方法[6]。因为空间矢量调制是一种PWM调制方法，要想获得好的变换性能，需要保证PWM调制的高频性。但是该调制策略在实现过程中需要进行三角函数和复杂的复数运算，使得计算量过大。如果开关周期太短(调制频率太高)，那么数字信号处理器就难以胜任，必然要加大开关周期，降低调制频率，降低了变换器的性能。因此，研究一种简化的空间矢量调制算法，减小运算量、提高开关频率，从而提高变换器的性能，使得矩阵变换器尽早步入工业应用具有重大意义。

本文在传统空间矢量调制算法的基础上，通过分析推导，将整流级电流空间矢量的占空比用三相输入相电压值来计算，将逆变级电压空间矢量的占空比用三相参考输出线电压值来计算，避免了传统算法中的三角函数计算，从而使得算法大大简化，提高了运算速度。另外，为了使得在各扇区内占空比的表达式统一，便于编程实现，对传统的扇区进行了重新定义，并给出了新扇区情况下占空比的统一表达式。最后应用Matlab/Simlink进行了仿真，证明了所提出的控制策略的正确性。

1 矩阵变换器空间矢量调制原理简介

矩阵变换器的拓扑结构如图1(a)所示，由三行三列的开关组成一个3×3的开关矩阵。输入三相电压源ua、ub、uc经过三相输入滤波器Lf、Cf后，给变换器供电，变换后输出的三相电压uA、uB、uC供给三相负载。

图1 矩阵变换器的拓扑

矩阵变换器的等效拓扑结构如图1(b)所示，由虚拟的整流环节和逆变环节组成。等效拓扑上的控制思想是首先对输入电压进行“整流”，以产生一个虚拟的直流环节，然后再对其进行“逆变”，逆变出所需频率和幅值的输出电压。

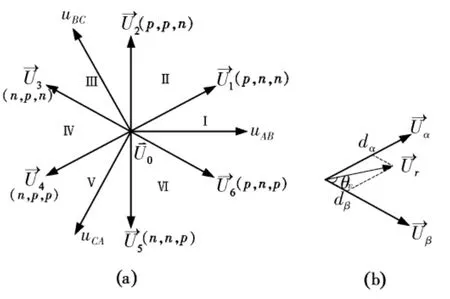
图2 逆变级空间矢量调制

矩阵变换器的空间矢量调制法[1]是一种双空间矢量的调制方法，该方法对矩阵变换器等效模型的整流级和逆变级分别应用电流空间矢量和电压空间矢量进行调制，得到正弦的输入电流、可调的输入功率因数和正弦的输出电压，然后将二者合而为一。

图1(b)所示逆变级的6只开关管分别有8种开关状态，每个开关状态用(xxx，x=p or n)来表示，分别代表输出(A，B，C)相桥臂的上桥臂导通(p)或下桥臂导通(n)。8个开关状态分别对应输出电压的8个电压空间矢量，如图2(a)所示。

三相参考输出电压可以合成一个电压矢量[1]，当参考输出电压矢量位于某一扇区内时，可用该扇区相邻的2个开关电压矢量和零矢量来合成，如图2(b)所示，矢量合成公式为:

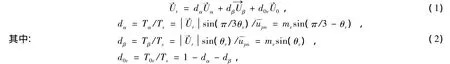
式中:mv为电压调制比;θv为的夹角;Ts为开关周期;Tα、Tβ、T0v和 dα、dβ、d0v分别为对应矢量的时间和占空比。

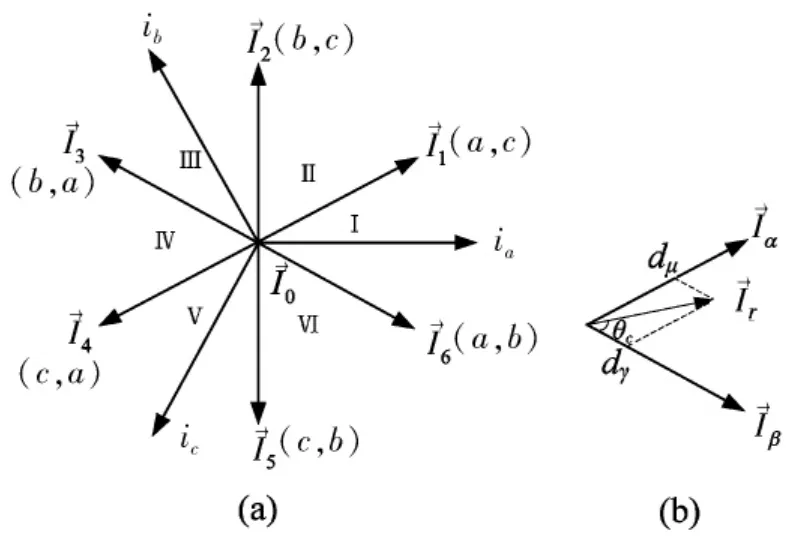
图3 整流级空间矢量调制

整流级的调制方法与逆变级相似，逆变级的6只开关管也分别有8种开关状态，每个开关状态用括号内的两位字母来表示，分别表示输入相与直流的p、n极的连接。例如(a，c)表示a相与p极相连，c相与n极相连。8个开关状态分别对应输入电流的8个电流空间矢量，如图3(a)所示。

式中:mc为电流调制比;θc为的夹角;Tμ、Tγ、T0c和 dμ、dγ、d0c分别为对应矢量的时间和占空比。

将整流级和逆变级进行综合并消去中间直流环节，得到矩阵变换器九个开关的控制规律，其综合后的合成占空比为:

2 空间矢量调制算法的简化

从上面的介绍空间矢量调制算法可以看出，在计算过程中存在复杂的正弦函数、反正切函数的计算(求θv和θc时[7])。而且在每个区间，都要有不同的变量处理，表达式不统一，为此下面研究一种简化算法。

假设输出三相参考电压的表达式为:

那么其线电压波形如图4所示，与图2(a)中相对应的区间划分如图所示。

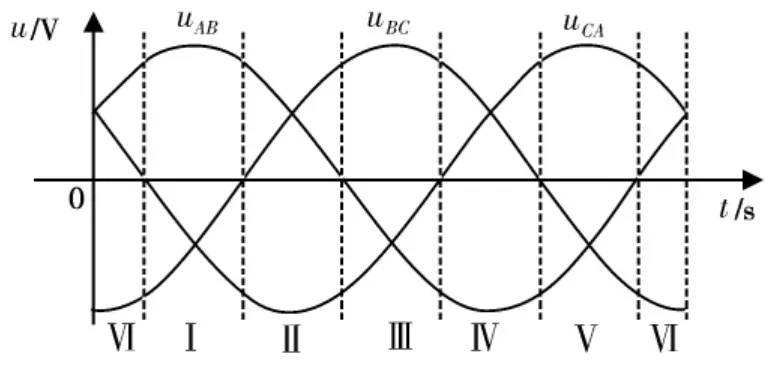
图4 输出电压区间划分

由图4可知，在I区间内θv=，代入公式(6)可得:

根据三相输出相电压的表达式以及相线电压的关系可得:

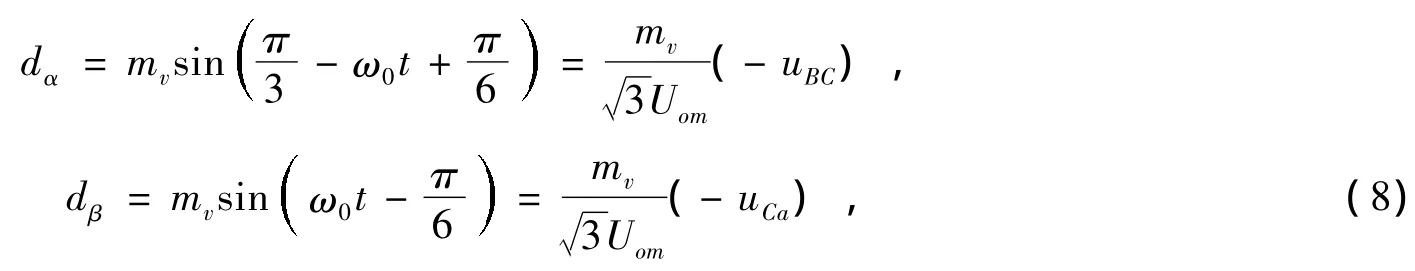
经过推导，对于占空比的计算可以直接用参考线电压的瞬时值来计算。同样，经过分析，在其他区间的占空比见表1，表中g=。

表1 逆变级占空比计算表达式

由上表可以看出，在各个扇区内，占空比的计算式是各不相同的。为了使占空比的表大会统一，便于实际编程，现对电压区间重新划分，如表1中最后一列所示，并定义如下的输出电压数组:

经过研究发现，占空比的表达式可以统一表示为:

式中:abs()为取绝对值函数，mod()为求余函数。

对于整流级研究分析以后，发现对于占空比的计算同样可以用输入电压来计算，各个区间的占空比如表2所示，表中k－mc/uim。

表2 整流级占空比计算表达式

同样，为了占空比的统一表示，对输入电流区间重新划分，如表2中最后一列所示，并定义如下的输入电压数组:

经过研究发现，整流级占空比的表达式可以统一表示为:

3 计算量对比

在空间矢量传统算法中，计算占空比共需要进行4次正弦函数计算，为了判断扇区，整流级和逆变级要进行复数计算来合成矢量[7]，而且为了获得θv、θc要进行2次反正切函数计算。可见，在传统算法中，计算量是比较大的。在简化算法中，占空比的计算用输入电压值和参考输出线电压值来计算，只需要进行简单的乘法运算。这些电压值都是实际系统中必须要测量的或者是已知的(如开环控制系统中的参考输出线电压)，并不会增加系统的负担。由于简化算法中，并不需要用到θv、θc，所以扇区的判断可以用电压的瞬时值大小来判断[7]，避免了复数和反正切函数运算，大大简化了算法的计算量。至于占空比统一算法中的求余运算，在实际编程时，可以用做减法后判断是否大于零来判断。综上所述可见，简化算法的计算量要远小于传统算法的计算量。

4 仿真分析

本文基于Matlab/Simulink建立了仿真模型，对提出的简化算法进行了仿真。仿真参数如下:输入电网频率为50 Hz，相电压幅值为311 V;输入滤波电感、电容分别为0.2 mH、30 μF;输出三相电压频率为100 Hz，相电压幅值设定为260 V;负载为三相对称负载，每相电阻为5 Ω，电感为5 mH;采样频率为10 kHz，仿真算法为 Ode23 t。

图5(a)是A相输出电压的波形，对其进行FFT分析，其频谱如图5(b)所示，可见输出电压中所含的谐波非常小，计算到80次谐波，A相输出电压THD为1.90%。A相输出电压的基波幅值为257.2，比设定的幅值略小，这主要是因为输入滤波器和IGBT导通电阻上的电压损耗造成的。B、C两相的输出电压与频谱分析与A相有类似的仿真结果，为节约篇幅，不再给出波形。

图5 输出A相电压及其频谱分析

图6给出了三相输出电流的波形，可见由于阻感负载的滤波作用，三相电流是比较好的正弦波。

图7是a输入电压和电流的波形，可见输入电流是正弦波，且与输入电压基本同相位，电流略微超前于电压，这是由于输入滤波器在低频段呈微小电容特性造成的[7]。

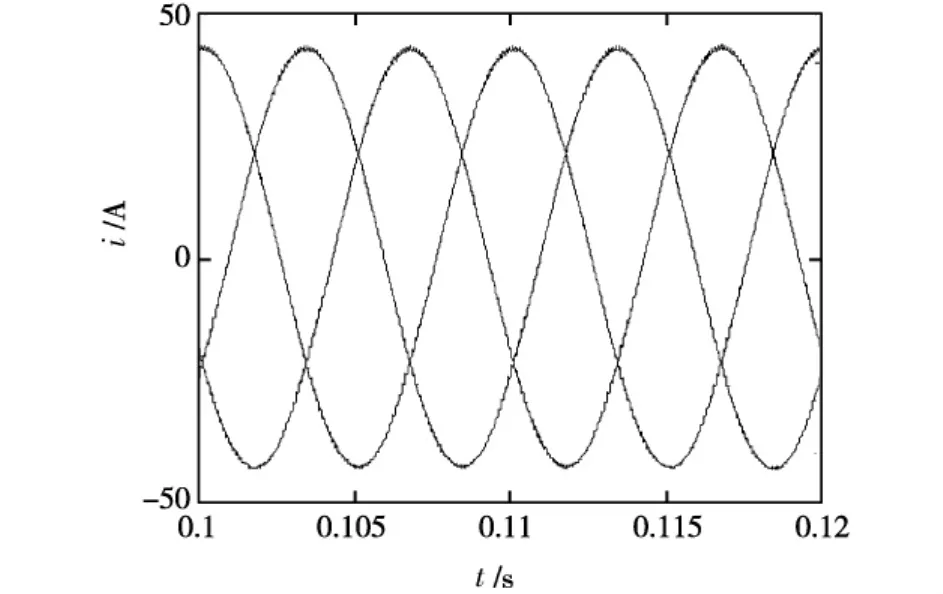
图6 三相输出电流

图7 输入a相电压和电流

由上述仿真结果可以看出，应用空间矢量简化控制算法，同样可以实现矩阵变换器的变压变频功能，而且具有优良的输入输出的性能。

5 结 论

矩阵变换器控制算法的复杂性限制了其在实际中的应用，研究一种简化算法，减小计算量、提高开关频率、保证矩阵变换器输入输出波形的质量，是矩阵变换器迈向工业应用所必须要解决的关键问题之一。本文通过对传统算法的分析研究，将整流级和逆变级的占空比分别用三相输入电压值和三相参考输出电压值来计算，避免了复杂的正弦函数、反正切函数和复数计算。通过扇区的重新定义，使得占空比表达式具有统一的形式，便于实际编程实现。简化算法大大提高了运算速度，减轻了数字信号处理器的负担，保证了矩阵变换器优良的输入输出性能，仿真结果验证了本文提出方法的正确性和有效性。

[1]Huber L，Borojevic D.Space vector modulated three-phase to three-phase matrix converter with input power factor correction[J].IEEE Transactions on Industry Applications，1995，31(6):1234 －1246.

[2]K.Oka，K.Matsuse.A Robust Current Control Method with Disturbance Observer for Matrix Converter Under Abnormal Input Voltage[J].IEEJ Trans.on Electrical and Electronic Engineering，2007，2(4):476 ～478.

[3]权建洲，吴保芳，孙容磊，等.基于前馈补偿的SPWM矩阵变换器控制策略研究[J].中国电机工程学报，2006，26(5):88－94.

[4]陈希有，陈学允.基于Park变换的空间矢量调制矩阵变换器的暂态分析[J].中国电机工程学报，2000，20(5):80－84.

[5]王汝田，王建赜，谭光慧，等.不平衡负载情况下矩阵变换器的拓扑改进及控制策略[J].中国电机工程学报，2008，28(36):33－39.

[6]黄科元.矩阵式变换器的空间矢量调制及其应用研究[D].杭州:浙江大学，2004.

[7]王汝田.矩阵变换器调制策略的研究[D].哈尔滨:哈尔滨工业大学，2009.