基于改进粒子群算法的负荷优化调度

马汝东，陈 婷，王建国，杨淑萍

(1.东北电力大学 自动化工程学院，吉林 吉林 132012;2.大唐长春第三热电厂 电控分厂，长春 130103，3.白城供电公司，吉林 白城 137000)

火电厂经济运行的最终目的，就是在保证电力负荷需要的前提下，使全厂总的发电成本最低，从而使全厂获得最大的经济效益。在得到电网公司的负荷调度后，发电厂商按所分配调度的负荷数量组织生产[1]。鉴于电厂的大型化、现代化和调峰问题的日益突出，机组不可能全部在经济工况下运行，需要通过经济调度达到整个火电厂的经济运行[2]。自80年代开始，我国将供电标准煤耗作为火电厂技术完善程度和运行经济性的国家考核指标。因此，火电厂经济运行的关键是通过对各台机组的优化调度，使机组供电煤耗最低，保证全厂的总能耗最小，这也是目前电力企业节能的重点。

自二十世纪三十年代提出机组负荷优化分配以来，在优化理论方面，科学工作者做了大量的研究工作，提出了许多有效的算法，主要有:传统优化方法(效率法、等微增率法、热化做功系数法)、最优化方法(线性规划法、非线性规划法、动态规划法)、现代优化方法(遗传算法、模拟退火算法、神经网络算法)、生物智能算法(蚁群算法、粒子群算法)等[3－9]。常见的厂级负荷优化分配系统使用等微增率法，该方法简单易行，但要求机组的煤耗特性曲线连续上凹且无拐点，实际的煤耗特性曲线很难满足，而且无法进行机组启停的优化;智能化方法对优化问题的数学模型和目标函数要求低，允许出现多种非线性和不连续因素，而且可以方便的处理各种约束条件，因此较适于解决高维、复杂的负荷优化分配问题。本文将粒子群算法引入到电厂负荷优化调度问题的研究，且全面考虑了机组调度的约束条件，如最小连续运行及停运时间、启停耗量约束等，通过对粒子群粒子的设置，将机组启停状态信息包含进去，不仅实现了机组负荷优化的分配，而且对机组启停也进行了优化;将粒子群算法的计算结果与传统的等微增率法及平均分配方法进行比较，本文算法更加科学合理。

1 数学模型的建立

考虑机组运行的实际情况，本文确定的机组约束条件包括功率平衡约束、机组出力约束、最小连续运行时间约束、最小连续停机时间约束，且考虑机组的启停损耗及寿命损耗，经过优化算法得到机组的启停优化及负荷分配。因为本文只涉及厂内负荷优化调度，且只需给出稳态的优化调度结果，故模型可不考虑网损和对应机组的爬坡速度约束;网损由中调考虑，爬坡速度可以由机组CCS限速模块(或运行人员经验)控制完成[10]。

设全厂机组的煤耗特性可用二次型函数表示:

其中，ai、bi、ci为第i台机组的煤耗特性系数;Fi为第i台机组的煤耗;fi(Pi)为第i台机组的煤耗特性方程;Pi为第i台机组的负荷。

设有n台机组可以投入运行，全厂总负荷为PTotal。优化调度的目的是将总负荷合理的分配到各台运行的机组上，使全厂的煤耗量最小，目标函数为:

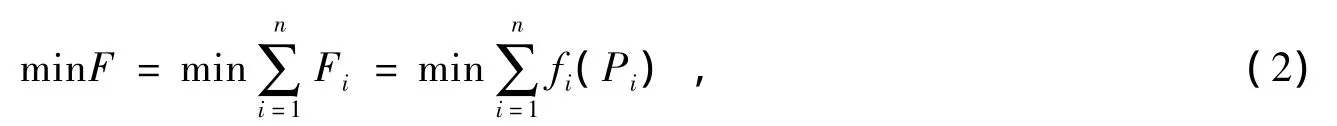
约束条件如下:

式中，Ui为第i台机组的运行状态，可取1(代表运行)或0(代表停机);Pi，min、Pi，max分别为第i台机组的负荷下限、上限;Ti，R、Ti，S为第i台机组的连续运行时间、停机时间;TRun、TStop分别为机组的最小运行时间、最小停机时间。

本文将启停耗量及寿命损耗都折算成煤耗量处理并加到每次启、停机组的消耗上，属于额外煤耗。因此，需要计算一段时间内煤耗量，将这段时间内的煤耗量加上有可能产生的额外煤耗量作为目标函数，求得其最小值，此时的优化调度结果才为最优调度。本文选择最小连续运行时间为计算区间，得到如下目标函数表达式:

式中，Ui、BUi分别为当前时刻及上一调度时刻机组i的启停状态;Losti为第 台机组启停时的损耗。

2 改进粒子群算法

粒子群算法为通过模拟鸟群觅食行为发展而来的一种基于群体和适应度的全局优化算法。在粒子群算法中，每个优化问题的潜在解都是搜索空间中的一个粒子的位置，粒子追随着当前的最优粒子在解空间中进行搜索。在每次迭代中粒子通过跟踪两个“极值”来更新自己:一个是粒子本身找到的最优解，另一个是整个种群目前找到的最优解。

设在一个D维的搜索空间中，粒子i的位置和速度分别表示为xi=(xi1，xi2，…xiD)和Vi=(vir，vi2，…viD)，其中 i=1，2，…，n，n 为种群规模。

图1表示了优化调度算法的整个流程，其粒子种群的配置上，鉴于负荷优化调度涉及到机组的启停优化问题，必须将机组的启停信息加入到粒子群中，这样每个粒子的位置将会包括四类信息，分别是机组运行状态U、机组当前出力P、每台机组的煤耗量Y。其中，机组运行状态S先取随机变量0或者1，然后再根据图2的时间约束程序计算将来可能的机组启停状态。

对于约束条件，采用构造罚函数的方法，将约束计入目标函数中，设罚函数为PF，则

式中，C为约束的罚系数。适应度函数变为

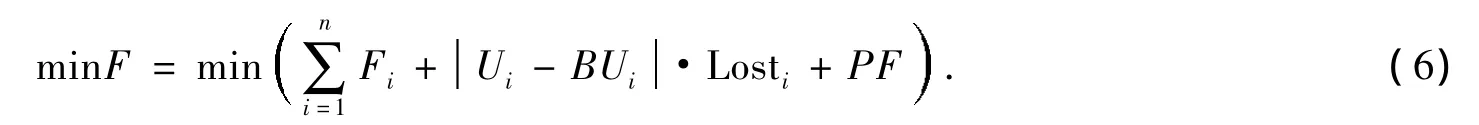
图1 厂级负荷优化调度算法程序流程框图

图2 时间约束程序流程框图

3 算例与比较

作为对比，本文选用文献[11]中四台机组的煤耗特性曲线，四台机组的煤耗曲线方程及其出力约束如下:

改进粒子群算法中参数设置如下:

粒子群大小Psize=10;最大迭代次数gmax=500;惯性权值 wmax=0.9，wmin=0.1;权重系数 c1=c2=2。当总负荷为550 MW时，改进粒子群算法的收敛曲线如下图3所示，在迭代到180代左右就已经稳定在最小煤耗量了。本文分别用改进的粒子群算法与传统的等微增率准则、常规粒子群算法进行优化计算作对比，其计算结果如下表1所示。

分析表1中数据可得，在总负荷PD一定下，等微增率准则只能在现有机组全部运行下，进行负荷分配;智能算法中的常规粒子群算法优化结果与等微增率准则的计算结果相差不大;而使用改进的粒子群算法，可以进行机组启停的优化的同时进行负荷分配，且全厂总煤耗量比使用等微增率准则的煤耗量低。

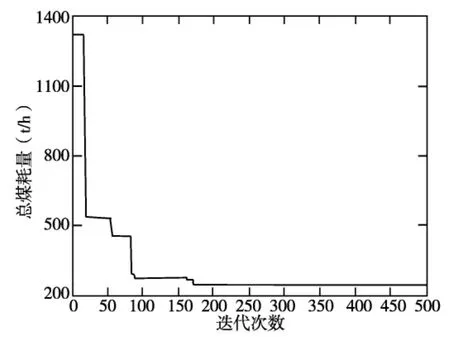
图3 改进粒子群算法的收敛曲线

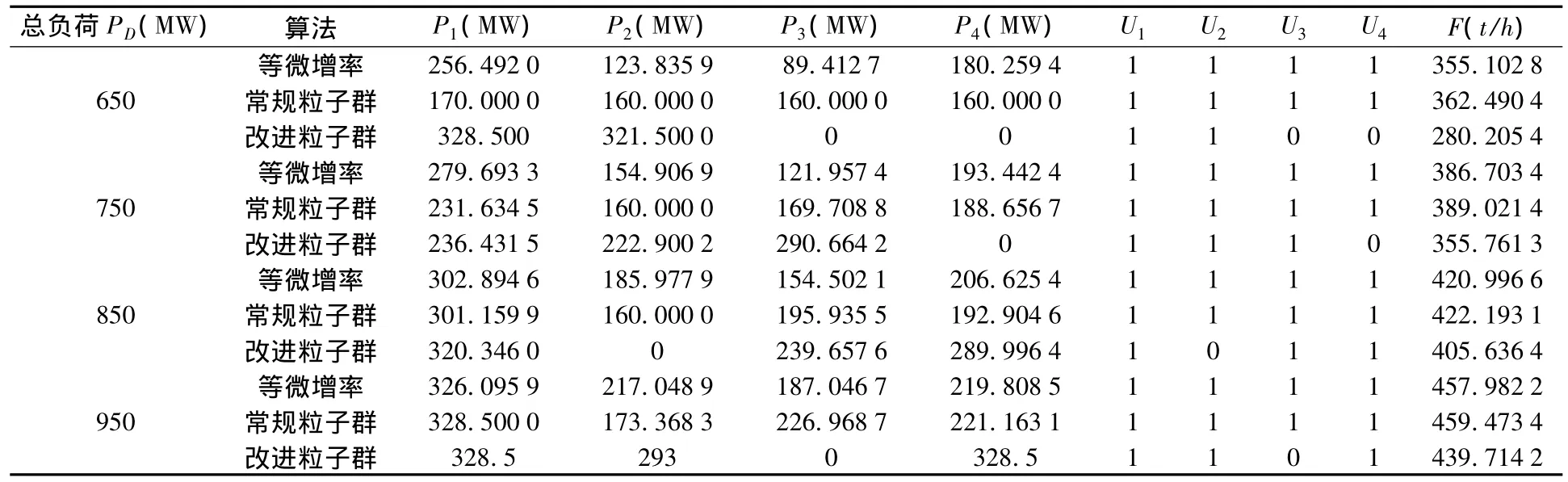
表1 等微增率准则、常规粒子群算法及改进粒子群算法下负荷优化调度结果对比

4 结 论

本文以机组煤耗特性为基础建立全厂煤耗最小的目标函数，并全面考虑机组调度的约束条件，如最小连续运行及停运时间、启停耗量约束等，利用改进的粒子群算法进行负荷优化调度，得到机组的启停优化及负荷分配，与传统的等微增率准则相比，全厂总煤耗量更低。

[1]周明.Hopfield神经网络及其在经济负荷分配问题中的应用[D].湖北:武汉大学，2005.

[2]肖增弘，王中利，王雷.火电厂多机组负荷优化分配的研究[J].沈阳工程学院学报，2011，7(2):111－113.

[3]A.Y.ABDELAZIZ，S.F.MEKHAMER，M.A.L.BADR，et al.Economic Dispatch Using an Enhanced Hopfield Neural Network[J].Electric Power Components and Systems，2008，36(7):719 －732.

[4]S.F.MEKHAMER，A.Y.ABDELAZIZ，M.Z.KAMH，et al.Dynamic Economic Dispatch Using a hybrid Hopfield Neural Network Quadratic Programming Based Technique[J].Electric Power Components and Systems，2009，37(3):253 －264.

[5]唐英干，崔玉红，关新平.动态粒子群算法在经济负荷分配中的应用[J].计算机仿真，2009，26(8):242－245.

[6]张智晟，林涛，王坤，孙雅明.电力系统经济负荷分配的量子粒子群算法[J].电工电能新技术，2008，27(4):1－4.

[7]Titus，S，Jeyakumar，A.Ebenezer.A Hybrid EP-PSO-SQP Algorithm for Dynamic Dispatch Considering Prohibited Operating Zones[J].Electric Power Components ＆ Systems，2008，36(5):449 －467.

[8]黄文成，谢刚.基于免疫思维进化算法的机组负荷优化分配[J].机械工程与自动化，2008，150(5):38－40.

[9]杨鑫.多智能体进化算法在火电厂负荷优化分配中的应用[D].北京:华北电力大学，2008.

[10]万文军，周克毅，胥建群，徐啸虎.动态系统实现火电厂机组负荷优化分配[J].中国电机工程学报，2005，25(2):125－129.

[11]刘星.基于遗传算法的火电厂厂级负荷经济调度的研究[D].北京:华北电力大学，2007.