采用模糊控制实现不确定混沌系统投影同步

赵 磊，姚 聪，刘胜荣

（1.黄山学院信息工程学院，安徽黄山245041；2.化学工业第二设计院宁波工程有限公司，浙江宁波315040）

采用模糊控制实现不确定混沌系统投影同步

赵 磊，1姚 聪，2刘胜荣1

（1.黄山学院信息工程学院，安徽黄山245041；2.化学工业第二设计院宁波工程有限公司，浙江宁波315040）

当驱动系统和响应系统参数未知和不确定时，研究不同混沌系统的投影同步，采用Takagi-Sugeno(TS)模糊动态模型和Lyapunov稳定性理论，导出了混沌系统广义投影同步的一个充分条件。通过一些矩阵操作技巧，这个准则被转化为一组线性矩阵不等式形式，并用Matlab工具箱方便地解决了这些线性矩阵不等式的求解。对Lorenz方程和Rossler系统的数值模拟，仿真结果表明该方法的有效性。

混沌；广义投影同步；模糊控制

1 引言

自从Pecora和Carroll[1]的驱动-响应同步方法提出以后，这十多年来，混沌同步由于其在保密通信、生命科学和信息等领域的潜在应用价值引起了非线性科学研究者的广泛关注，文献中已经提出了许多有效的混沌控制与同步的方法。[2-4]同时，对混沌系统同步现象的研究也取得了一定的成果。如混沌系统完全同步、混沌系统的相位同步、广义混沌系统同步和混沌系统延迟同步等。1999年，R.Mainieri和J.Rehacek[5]在研究部分线性混沌系统中观察到了一种新的同步——投影同步，即在耦合某些部分线性混沌系统时，一定条件下耦合的主从系统状态的输出不仅相位锁定，而且各对应状态的振幅还按某一比因子关系演化。随后Xu等人对混沌系统的投影同步现象进行深入研究，提出了三维混沌系统同步的稳定标准，任意维连续混沌系统出现投影同步的判断准则以及任意维离散混沌系统出现投影同步的必要条件。[6，7]

到目前为止，国内外学者提出了许多基于精确模型的混沌系统控制策略。[8-11]然而当混沌系统模型不确定或者部分甚至所有参数未知时，这些方法就失效了。在控制系统设计中，最关键且又最困难的是如何针对复杂、变化而且不确定性的受控对象和环境，做出有效的控制决策。同时，由于混沌系统对初始条件的敏感性，那么，对不确定混沌系统的控制和同步将更加不易。由于模糊逻辑已证明具有对非线性系统任意逼近的特点，把模糊逻辑和混沌系统结合起来，本文提出了采用模糊控制实现不确定混沌系统投影同步的控制方法。为说明本文方法的有效性，考虑了Lorenz方程和Rossler混沌系统的广义投影同步控制问题，仿真结果表明，本文的方法是有效的。

2 混沌系统的投影同步

考虑连续系统，其不确定TS模糊动态模型为：

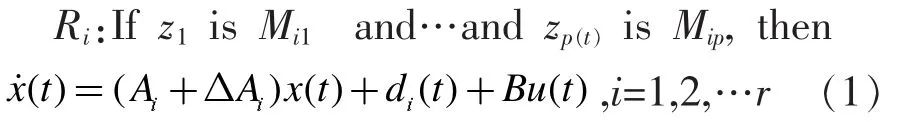
式中Ri表示模糊系统的第i条规则，Mij(j=1,2…，p)是模糊集合，r是模糊推理规则数，x(t)∈Rn是状态变量，z1(t),z2(t),…zp(t)是模糊前件变量，u(t)∈Rm是控制输入。Ai，B是第i个子系统相应维数的矩阵，△Ai表示参数摄动，di(t)表示外扰动，它们满足如下匹配条件：

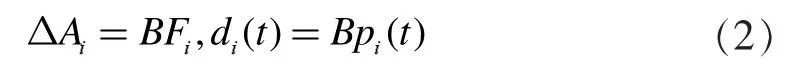
其中Fi是未知矩阵，pi(t)为未知有界函数，满足：

这里ωi和ξi是未知常数。

假设1：存在矩阵A0使得Ai-A0=BGi(i=1,2,…，r)，这里Gi是已知矩阵。

若采用单点模糊化，加权平均反模糊化方法，（1）式可以表示成如下全局系统方程

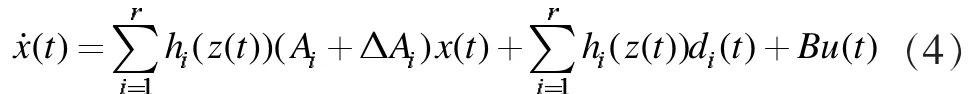
μij（(t)）是zj(t)关于模糊集Mij的隶属函数，wi（z(t)）满足：

同时参考模型也是一不确定混沌系统，其T-S模糊动态模型为：

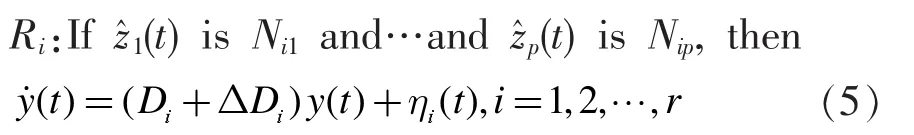
式中Nij(j=1,2…，p)是模糊集合，r是模糊推理规则数，y(t)∈Rn是状态变量，(t)是模糊前变量，Di是第i个子系统相应维数的已知参数矩阵，△Di表示参数摄动，ηi(t)表示外扰动，它们满足如下匹配条件：

假设2：存在矩阵D0使得Di-D0=BRi(i=1,2,…，r)，这里Ri是已知矩阵。

采用类似上面的方法可得到参考模型（5）的全局系统方程为：

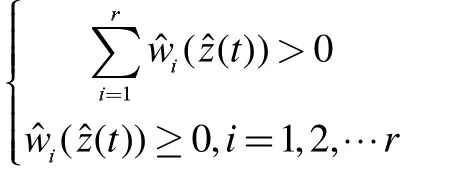
定义误差向量为e(t)=αx(t)-y(t)，其中α为尺度因子，结合系统（4）和（7）得：

由假设1和假设2，（8）式可以写成：

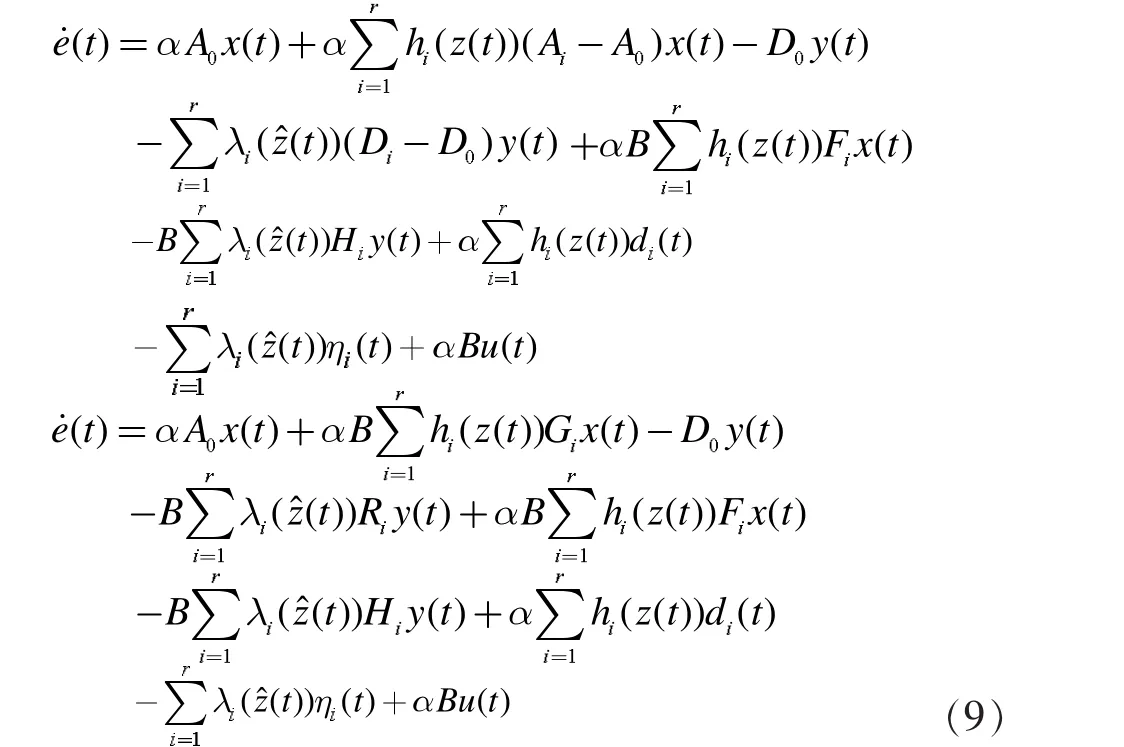
根据系统模型构造控制器u(t)为：

其中

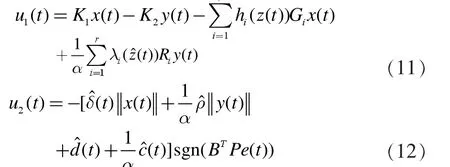
这里P∈Rn×n是一个待求的正定矩阵，K1∈Rn×n，K2∈Rn×n，sgn表示符号函数，δ(t),p^(t),c^(t)和d^(t)满足自适应调解律，即

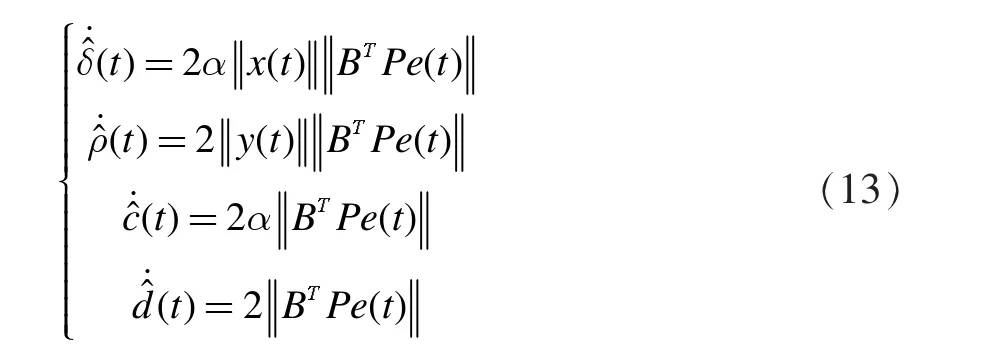
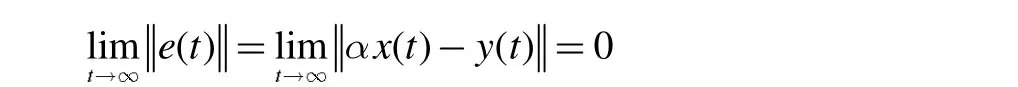
则混沌系统（1）和（5）为广义投影同步。

假设3：存在矩阵K1和K2使得

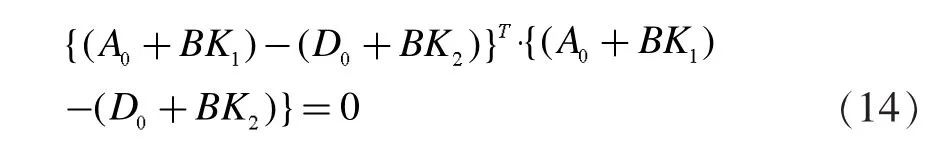
定理1：在假设1,2,3下，若存在正定矩阵P和矩阵K1使得

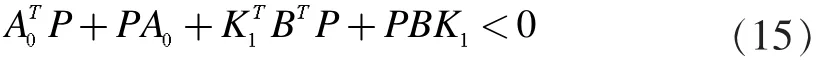
证明：将（10）式代入（8）式得闭环系统

在假设3下，系统（16）还可以写成

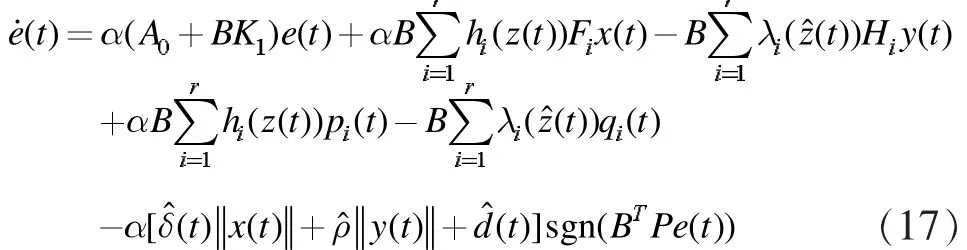
构造一个Lyapunov函数

tere kümün öɡdör(ööɡedör)tere tuqai ü (那个人昨天就把那件事说了)

对V(t)关于时间t求导得

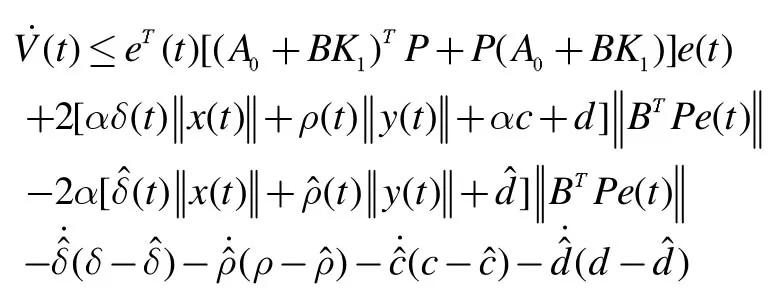
采用自适应律（13）式，进一步化为：

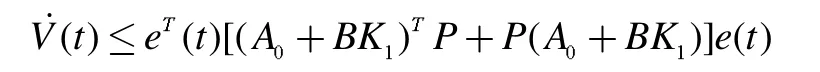
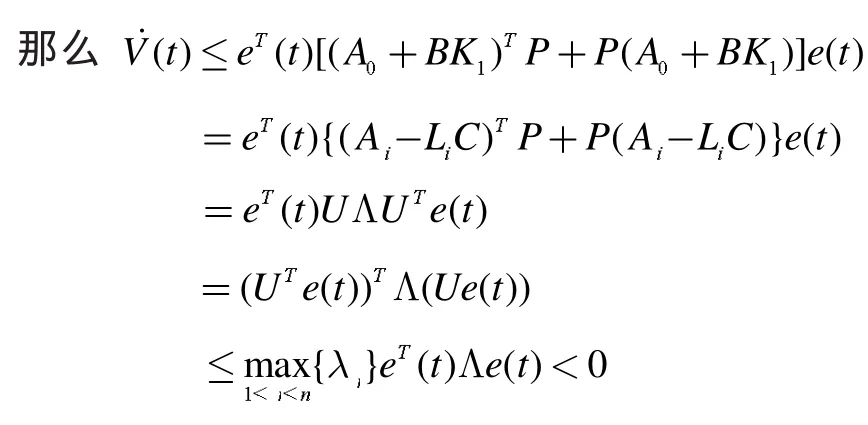
假设(14)式可以转化为求解

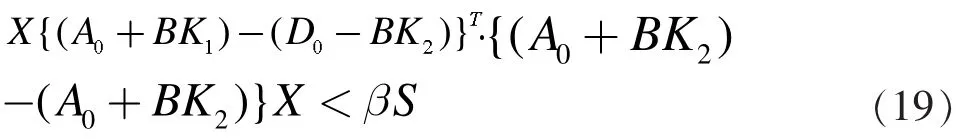
这里X和Y是两个正定矩阵，且STS＜I。

令P=X-1和Yi=KiX，i=1,2,则定理1中控制u(t)的设计问题转化为如下不等式求解问题：

3 数值仿真

考虑如下的Lorenz方程

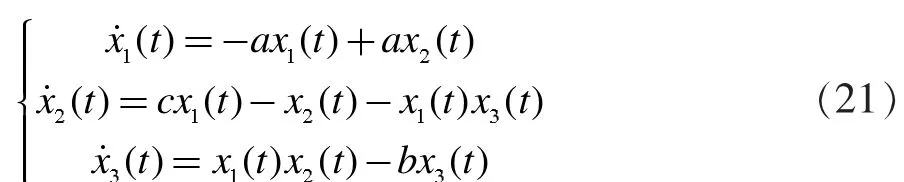
当a=10,b=8/3,c=28时系统呈混沌态，由于混沌系统的有界性，我们假设系统的状态x1(t)∈[-θ,θ]，其中θ＞0都呈混沌态。根据系统（1）,Lorenz的TS模糊模型可表示为

R1：如果z(t)是M1；则

R2：如果z(t)是M2；则

其中x(t)=[x1(t),x2(t),x3(t),]T,

参考模型为Rossler混沌系统，假设系统的状态y1(t)∈[4.5-θ,4.5+θ]，根据系统（5）,Rossler的TS模糊模型可表示为：

R1：如果z^(t)是M1；则

R2：如果是M2；则

选取A0=A1和D0=D1，根据定理1，应用Matlab软件的LMI工具箱可求得满足条件（20）的矩阵为

设初始条件x(0)=[0.1,0.1,0.5]T，y(0)=[0.2,0.1,0.6]T，选取，仿真结果分别如图1所示：

图1 Lorenz方程和Rossler混沌系统在的广义投影同步

4 结论

本文研究了由TS模糊模型表示不确定混沌系统的广义投影同步，给出了一种简单有效的控制方法，该方法利用线性矩阵不等式技术，把系统的稳定性条件转化成对一组线性矩阵不等式的求解问题。本方法构造简单，同步速度快，精度高，且仿真结果表明该方法是有效的。

[1]Pcora L M,Carroll T L.Synchronization in chaotic systems[J].Phys.Rev.Lett,1990,64(8):821-823.

[2]赵磊,赵雪峰,郑永爱.采用模糊控制实现混沌系统的广义投影同步[J].电机与控制学报,2007,11(6):644-647.

[3]孟娟，王兴元.基于模糊观测器的Chua混沌系统投影同步[J].物理学报,2009,52(2):413-416.

[4]Kazuo T,Takayuki I and Wang.H O.A unified Approach to Controlling Chaos via an LMI Based Fuzzy Control System Design[J].IEEE Trans.Circ.Syst,1998,45(10):1021-1040.

[5]Mainieri R and Rehacek J.Projective synchronization in Three-Dimensional chaotic system[J].Phys Rev Lett,1999,82(15):3042-3045.

[6]Xu D L.Control of projective synchronization in chaotic systems[J].Phys Rev Lett,2001,63(2):027201(1-4).

[7]Wen G L,Xu D L.Nonlinear observer control for fullstate projective synchronization in chaotic continuos-time systems[J].Chaos Solitons and Fractals.2005,26(1):71-77.

[8]Yan J P,Li C P.Generalized projective synchronization of a unified chaotic system[J].Chaos Solitons and Fractals,2005,26(4):1119-1124.

[9]L i G H.Generalized projective synchronization of two chaotic systems by using active control[J].Chaos Solitons and Fractals,2006,30(1):77-82.

[11]赵磊,郑永爱.基于模糊观测器混沌系统的广义投影同步[J].控制工程,2007,14(6):622-624.

责任编辑：胡德明

Abstact:This paper presents projective synchronization between two different chaotic systems when the parameters of the drive and response systems are unknown and uncertain.Based on Takagi-Sugeno(TS)fuzzy dynamical models and the Lyapunov Stability Theory,a sufficient condition is derived for the generalized projective synchronization of chaotic systems.By using some matrix operation techniques,this criterion is then transformed into linear matrix inequalities(LMI)form,which can be solved numerically using readily available Matlab software packages.The effectiveness of the proposed generalized projective synchronization method is illustrated through numerical simulations of the Lorenz equation and Rossler system.

Key words:chaos;generalized projective synchronization;fuzzy control

Realizing Projective Synchronization of Uncertain Chaotic Systems by Fuzzy Control

Zhao Lei1,Yao Cong2,Liu Shengrong1
(1.College of Information Engineering,Huangshan University,Huangshan245021,China;2.SEDIN,Ningbo Engineering Co,Ltd;Ningbo315040,China)

TP273

A

1672-447X（2012）03-0018-004

2011-11-06

黄山学院自然科学研究项目（2008xkjq016）；黄山学院自然科学重点项目（2011xkjq002）

赵磊（1981－），山西长治人，黄山学院信息工程学院教师，硕士，研究方向为非线性控制。