FANUC 0i数控系统车削二次曲线零件宏程序的应用*

赫焕丽(咸宁职业技术学院，湖北咸宁437100)

FANUC 0i数控系统车削二次曲线零件宏程序的应用*

赫焕丽
(咸宁职业技术学院，湖北咸宁437100)

在数控车削加工中，由于现代的数控系统中只有直线插补和圆弧插补指令，不适合二次曲线类零件的编程，因此二次类零件的加工是比较困难的，本文较全面总结了FANUC 0i数控系统车削加工二次类零件中宏程序的应用。采用切槽法使二次曲线的宏程序编程更加简便。

抛物线;宏程序;编程;应用

引言

在实际机械加工和各种数控大赛中，我们常常会遇到由抛物线、椭圆等构成的复杂二次曲线类零件，但目前的数控系统还没有提供完善的二次曲线插补功能，因此二次曲线编程是手工编程中的难点，因此，在实际加工中二次曲线的编程多采用变量来完成，也就是采用宏程序进行编程。宏程序的编制确实存在相当的难度，要想编制出一个加工效率高、程序简洁、功能完善的宏程序更是难上加难。下面我就以抛物线和椭圆曲线的宏程序编程为例，来研究用户宏程序在数控车削二次曲线类零件编程中的应用。

一、过程分析

如图1所示带内抛物线的套类零件，该零件外表面由圆柱面、椭圆等组成，内表面由圆柱孔、抛物线等组成，加工抛物线、椭圆时，须用宏程序编程，用直线或圆弧逼近曲线。

图1 非圆内孔加工

根据工艺分析，制定加工工艺路线如下:(1)采用三爪卡盘直接夹持毛坯左端，车端面、粗车外圆柱面至Φ46.5mm;(2)钻孔和扩孔;(3)用切槽刀径向进给，自右向左粗车椭圆及槽，留余量0.5mm;(4)粗车外圆柱面Φ36mm至Φ36.5mm;(5)精车外轮廓;(6)粗车内部抛物线;(7)精车内部抛物线;(8)用切断刀切断.

图2 坐标计算

由图2解析几何可知，该椭圆在XOZ坐标系内的标准方程为:+=1，易知A点编程坐标为(46，0)，将X= 15代入方程，可求得B点Z坐标ZB=－26.53，即B点编程坐标为(30，－26.53)，设椭圆上任意一点E在XOZ坐标系内的坐标值用变量表示为XE=#3，ZE=#4，代入上式，则有+=1。

用切槽法自右向左粗车椭圆，以#4为自量，则有#3= 23/35×SQRT［35×35－#4×#4×#4］，取#4的初始值为－5(不必取为0)，最终值为－26.53，在XOZ坐标系内，编程坐标XE=2×［#3］，ZE=#4，精车椭圆时，仍以#4为自变量，其初始值为0。已知抛物线在X1O1Z1坐标系内的标准方程为:Z1= 0，可知当Z1=24时，X1=20，当X1=6时，Z1= 2.16，设抛物线上任意一点F的坐标值用变量表示为XF=#1，ZF=#2，代入上式，则有#2=0.06×#12.抛物线上任意一点F的编程坐标值X=2×#1，ZF=#2－24.粗、精车抛物线时，用宏程序编程，以#1为自变量，可见#1的初始值为20，最终值为6.因此，在切削加工中，用切槽刀径向进给，采用宏程序编程.粗车椭圆及槽，用宏程序编程，沿轮廓进给，精车椭圆，最后切断。

由以上分析，编写该零件的加工程序如表1所示:

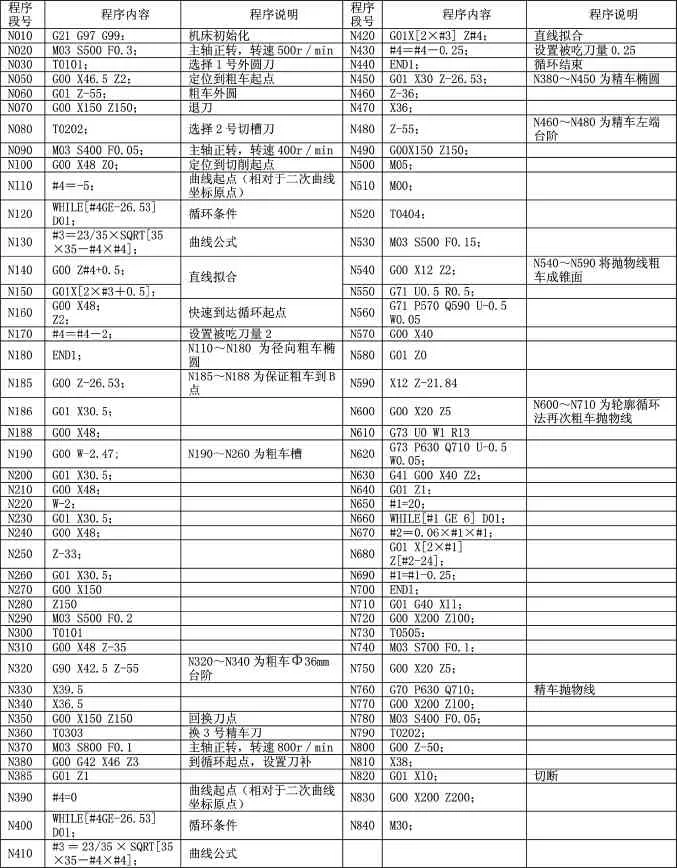
表1 参考程序程序号:O0001

二、总结

通过利用宏程序功能加工二次曲线零件，能充分的表明宏程序对于加工典型的二次曲线轮廓的效率。从我们上边的编程可以推广到已知零件轮廓方程的椭圆、抛物线等零件的编程中。因此，我们总结出以Z做为自变量的WHILE语句二次曲线加工模板如表2所示，以供大家参考。

表2 以Z做为自变量的WHILE语句二次曲线加工模板

TG519.1

A

2012－03－09