构造镶边幻方代码法的代码公式

王辉丰

（海南师范大学 数学与统计学院，海南 海口 571158）

构造镶边幻方代码法的代码公式

王辉丰

（海南师范大学 数学与统计学院，海南 海口 571158）

给出构造偶数n=2m（m=3，4，…为自然数）阶轴心双对称镶边幻方的代码公式及其证明，本代码法包括了已有的镶边法.

镶边幻方；代码法；代码公式；轴心双对称

文[1]和[2]介绍了构造幻方的镶边法，文[3]研究了镶边幻方，提出构造镶边幻方的代码法.通常为了构造任意n阶的幻方，就要先构造（或已知）一个原始n-2阶幻方.在这个幻方中，每个方格的数上加一个整数，然后在它四周镶上一条边，安装余下来的数字使之成为n阶幻方.镶边幻方就是用镶边法一圈加一圈形成的任意阶幻方，如果逐层地剥掉外圈，留下来的方阵仍然是一个个幻方，但数字不是从1开始的了.这种镶边法需要解决两个关键问题：一个是对原始幻方各方格中的数加一个多大的整数？已经知道，各方格的数都加一个整数是2（n-1）.另一个是余下的数如何安装到外层的方格中去？一般可以通过试探法经过调整达到目的，而没有统一的规则.本文得到用代码法安装外层数字的一般代码公式，不必反复试探，只由4阶核代方阵，按公式计算就可直接安装外层的数字（代码），不需要先构造（或已知）一个原始n-2阶幻方.这些公式与文[3]构成的代码法更加完善，包括已有的镶边法，完整地解决了镶边法的上述关键问题.下面讨论代码法的代码公式.

1 构造偶数阶轴心双对称镶边幻方的代码法

若偶数阶幻方中位于对角线上的数中心对称，位于正中的4阶幻方是中心对称幻方;轴对称与文[3]不同，偶数阶幻方不存在中间行、中间列，是以这类幻方的纵、横方向的中线为轴对称，即幻方位于两对角线之间上下的数，是以幻方的（与行平行）中线为轴对称，位于两对角线之间左右的数，以与列平行的中线为轴对称.为了与文[3]的双对称区别起见，把上述对称叫做偶数阶幻方的轴心双对称简称轴心双对称.

下面阐述构造n=2m（m=3，4，…为自然数）阶轴心双对称镶边幻方的步骤：

首先，设定代码

设以代码为元素的n=2m（m=3，4，…）方阵为A，a（i，j）（i，j=1，2，…，n）表示位于A的第i行，第j列的元素，A称为代方阵.把事先给定的中心对称的4阶代方阵作为待安装的n阶代方阵A的核心，这个4阶代方阵称为A的核代方阵.

第一步 安装代方阵A.

用代码法安装A外层的代码，这些代码所在行列的确定依赖于某参数的选择.设这参数为k，得到下列两组含有k的代码公式.由公式计算镶边行列的代码，由中心向外即按k由小到大的顺序安装代方阵A的各个元素.

若k为偶数，k由2开始至不超过m的最大偶数，取第（I）组公式（1）～（7）如下：

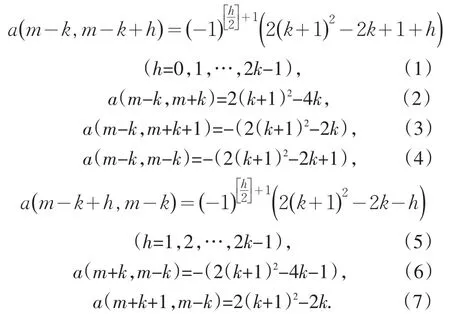
若k为奇数，k由3开始至不超过m的最大奇数，取第（II）组公式（8）～（13）如下：

此时，只是安装了代方阵A左上角（由左下角至右上角对角线以及其上方）的元素，接着，在轴心双对称的位置上安装相应的互补数（代码），就得以代码为元素的代方阵A.代方阵A以及其任一个大于4阶的同心的子方阵，它们的每行、每列和两条对角线上的代码之和都等于0，且具有轴心双对称性，但4阶核代方阵却是中心对称的.

第二步 还原代方阵A为方阵B.

把代方阵A中的代码换成（还原）其所表示的自然数，得到一个新的n=2m（m=3，4，…）阶方阵B就得轴心双对称镶边幻方（见定理1）.

对称段（两对角线所夹上下、左右）的元素互置，所得仍为对称镶边幻方，所以这种代码法可构造出2m-2·2m-2=22m-4个不同的n=2m（m=3，4，…）阶轴心双对称镶边幻方.

利用由构造上述n阶轴心双对称镶边幻方过程中所产生的低阶代方阵，通过还原相对应低阶代方阵，还可分别得到s=6，8，…，2m-2阶轴心双对称镶边幻方.

在证明定理之前，为了更好显示上述代码法的作用和意义，首先举例如下：

例1 构造一个12阶轴心双对称镶边幻方，并利用构造过程中所产生的低阶（如6阶、8阶、10阶）代方阵得出相应的低阶（6阶、8阶、10阶）轴心双对称镶边幻方.

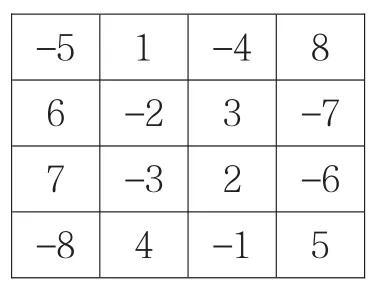
首先，给定一个12阶代方阵的4阶核代方阵（见图1）

图1 4阶核代方阵Fig.14-order core-code square matrix

然后，对此用代码公式进行镶边.

第一步 取k为偶数，当k=2时，由第（I）组公式（1）得

由此得

a（4，4）=-15，a（4，5）=-16，a（4，6）=17，a（4，7）=18；

由式（2）～（4）得

a（4，8）=10，a（4，9）=-14，a（4，4）=-15，

由式（5）得

由此得

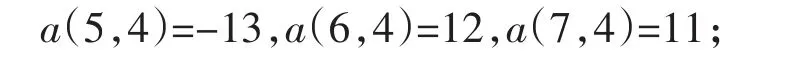
由式（6），（7）得

当k=4时，同样由第（I）组公式（1）～（7）顺序得

取k为奇数，当k=3时，同样由第（II）组公式（8）～（13）得

当k=5时，同样由第（II）组公式（8）～（13）得

将以上由（I）、（II）组公式计算得的aij安装（镶边）到图1得图2.

再在轴心双对称的位置上安装互为补数（代码）就得12阶代方阵（见图3）.

第二步 还原代方阵.

对于12阶幻方，自然数1～72，73～144的对应代码分别是-72～-1，1～72.把代方阵A中的代码换成其所表示的对应自然数，得到如下一个新的12阶方阵就是所求的轴心双对称镶边幻方（见图4）.

注 从例1更清楚看出代码公式中（3）与（7）为互补，（10）与（13）为互补；（1）包含（4），（8）包含（13）.（I）、（II）组公式之所以不精简，是为了以下定理1的证明更清晰起見.在计算时可以省略.

对称段的元素互置，所得仍为轴心双对称镶边幻方，所以可由此构造出26-2·26-2=256个不同的12阶轴心双对称镶边幻方.

由上述构造12阶轴心双对称镶边幻方过程中所产生的低阶代方阵，可得出相应的低阶轴心双对称镶边幻方.由图3中的6阶代方阵（见图5）的代码-18～-1，1～18所对应的自然数分别是1～18，19～36.代方阵中的代码换成其所表示的自然数,就得到一个6阶轴心双对称镶边幻方（见图6）.

同样可得8阶、10阶轴心双对称镶边幻方.

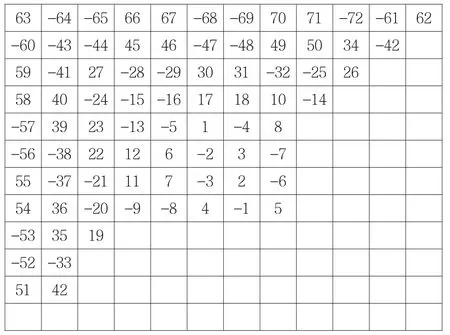
图2 12阶代码镶边方阵Fig.212-order code-bordered square matrix

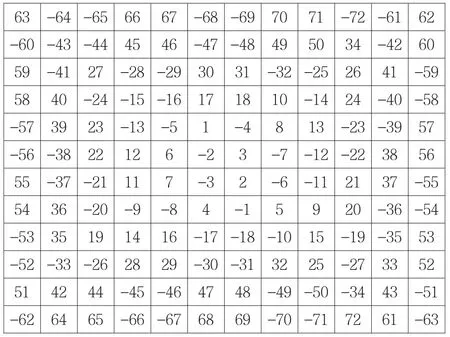
图3 12阶代方阵Fig.312-order code square matrix

图4 12阶轴心双对称镶边幻方Fig.412-order axial-centre double symmetrical bordered magic square

图5 6阶代方阵Fig.56-order code matrix square

2 定理证明

定理1 由代码法得的方阵B是一个n=2m（m=3，4，…为自然数）阶轴心双对称镶边幻方.

图6 6阶轴心双对称镶边幻方Fig.6 6-order axial-centre double symmetrical bordered magic square

证明 若k为不超过m-1的偶数，在代方阵A的任一个同心的2（k+1）阶子方阵，包括代方阵A左上角（左下角至右上角对角线以及其上方）中，代方阵A的第m-k行的2（k+1）（k=2，3，…，m-1）个元素之和为

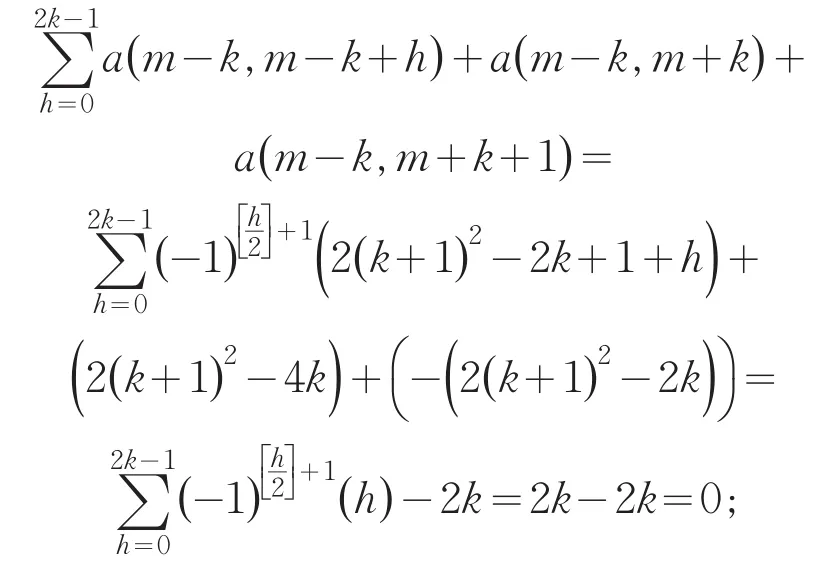
代方阵A的第m-k列的2（k+1）（k=2，3，…，m-1）个元素之和为

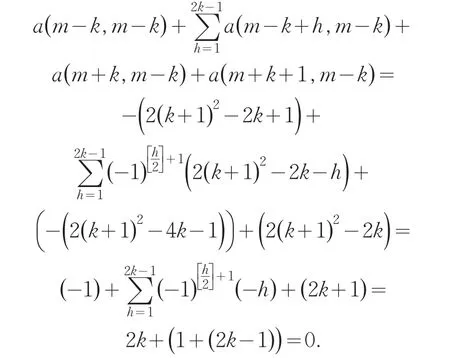
若k为大于1不超过m-1的奇数，在代方阵A的任一个同心的2（k+1）阶子方阵，包括代方阵A左上角（左下角至右上角对角线以及其上方）中，代方阵A的第m-k行的2（k+1）（k=2，3，…，m-1）个元素之和为

代方阵A的第m-k列的2（k+1）（k=2，3，…，m-1）个元素之和为

由于代方阵A的每一个代元都是按轴心双对称规则安装的，显然代方阵A的任一个同心的2（k+1）（k=2，3，…，m-1）阶子方阵，包括代方阵A，其每行、每列以及两条对角线上的代码之和都等于0，且具有轴心双对称性.当我们把代方阵A中的代码还原为所表示的自然数，所得新的方阵的任一个2（k+1）（k=2，3，…，m-1）阶子方阵，其每行、每列以及两条对角线上元素的和都等于相应的幻方常数，且具有轴心双对称性.所以，这样的方阵就是轴心双对称镶边幻方（是正规幻方）.定理证毕.

当我们以1～2（k+1）2依次代替代码-2（k+1）2～-1，同时以2（k+1）2+1～4（k+1）2依次代替代码1～2（k+1）2，相应地就得到2（k+1）（k=2，3，…，m-1）阶的轴心双对称镶边幻方（是正规幻方）.

上述代码法亦可用于已有镶边法，此时只需取参数k=m-1.

例2 对南宋杨辉易数图中的阳图[1]8阶幻方进行镶边.得到一个10阶镶边幻方.

杨辉易数图中的阳图为

图7 8阶杨辉幻方Fig.78-order YANG Hui magic square

由n=2m=10知，在图7中每个数都加2（n-1）=18，得到的方阵见图8.

因为m=5参数k=m-1=4为偶数，所以，同样由第（I）组（1）～（8）公式得

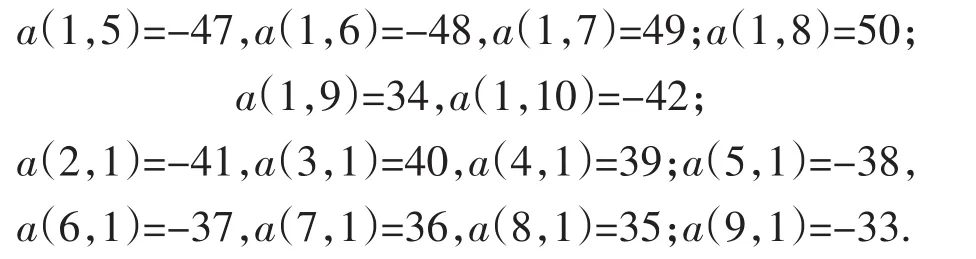
图8 8阶方阵Fig.88-order square matrix

将以上计算所得的代码安装到代方阵，在轴心双对称的位置上安装互为补数（代码），得10阶镶边幻方最外一圈的代码，见图9.

图9 10阶方阵外圈Fig.9 10-order square matrix periphery

注意到对于10阶方阵，1～50对应的代码为-50～-1；51～100对应的代码为1～50，把图9中的代码还原，换成与其相应的自然数，再把图8镶入其中，得到的10阶镶边幻方（见图10）.

图10 10阶镶边幻方Fig.10 10-order bordered magic square

由8阶幻方镶边生成10阶镶边幻方，又由10阶镶边生成12阶镶边幻方，如此继续，可生成2m阶镶边幻方.

[1]吴鹤龄.幻方及其他[M].北京:科学出版社,2004:21-22;76-78.

[2]詹森.你亦可以造幻方[M].北京:科学出版社,2012:221-231.

[3]詹森,王辉丰.关于构造高阶幻方的新方法[J].海南师范大学学报:自然科学版,2010,23(2):152-157.

责任编辑：黄 澜

The Code Formulas about Building Bordering Magic Square

WANG Huifeng
（College of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

The new code Formulas were given and proved,which included bordered method and could obtain a n=2m（m=3，4，…）order axial-centre double symmetrical bordered magic square.

bordered magic square；code method；code formulas；axial-centre double symmetrical

O 157.6

A

1674-4942（2012）03-0268-06

2012-05-09