构造高阶f次幻方的加法

詹森

（广东技术师范学院 计算机科学系，广东 广 州 510665）

构造高阶f次幻方的加法

詹森

（广东技术师范学院 计算机科学系，广东 广 州 510665）

给出构造高阶f（=1，2，…为自然数）次幻方的加法，并证明两个f次幻方的和仍是一个f次幻方；两个f次完美幻方的和仍是一个f次完美幻方.

幻方；加法；f次幻方；f次完美幻方

将一个幻方中的每个数都取2，3，…次幂，一般来说，所得相应的方阵不是幻方.如果一个幻方中的每个数都取遍f（f=1，2，…为自然数）次幂，所得相应的方阵仍然是幻方，则称这个幻方为f次幻方[1].若相应的方阵仍然是完美幻方，则称这个幻方为f次完美幻方.一次幻方就是常见的幻方.构造f次幻方是一件很困难的事，构造低阶f次幻方就更困难，这是世界上幻方研究者正在努力攻克的难题，2003年2月，高治源和潘凤雏合作编出2个12阶3次幻方，为下文方便，将其中一个幻方[2]记为CH.目前12阶3次幻方仍是最低阶高次幻方的世界记录.

1 构造高阶幻方加法的定义

根据文[3]构造高阶幻方的加法，我们可以利用两个已知的低阶f次幻方构造高阶f次幻方.

设给定m阶幻方为A，n阶幻方为B.以a（i，j）（i，j=1，2，…，m）表示幻方A的元素；以b（h，k）（h，k=1，2，…，n）表示幻方B的元素.我们利用幻方A、B构造一个mn阶幻方C，其待定的元素为c（i，j）（i，j=1，2，…，mn），这里C是用m个n2阶子幻方C（i，j）（简记 Cij=C（i，j）（i，j=1，2，…，m））安装而成，即令

其中这些子幻方Cij按如下步骤计算：

第一步：设一个n阶方阵为

则（-1）I是方阵I的每一个元素乘以（-1）所得的n阶方阵.将B与（-1）I的对应元素相加，它们的和记为，其元素为 b（h，k）-1（h，k=1，2，…，n），显然，仍是一个n阶幻方.

第二步：的每一个元素乘以m（2可归结为m2个相加）得的方阵记为，即

它的第h行，第k列元素为

显然，仍是一个n阶幻方.

第三步：由A的元素a（i，j）（i，j=1，2，…，m）构造n阶方阵如下：

为了方便起见，把一个方阵中所有元素都等于同一个数的方阵称为同元方阵，A（iji，j=1，2，…，m）都是同元方阵.令Cij=+Aij，则

幻方所有元素加同一个a（i，j）得到C（iji，j=1，2，…，m），它的元素为

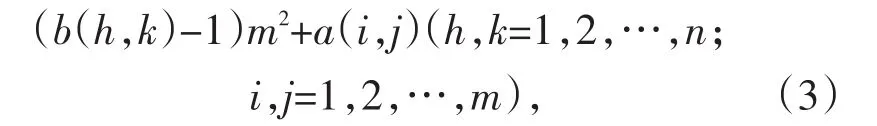
每一个Cij（i，j=1，2，…，m）都是n阶幻方.把这些幻方安装入（1）中，就得到一个方阵C，这就是所要构造的mn阶幻方.

我们把以上运算称为两个幻方的加法，以⊕表示，A⊕B表示A与B的和（幻方），记C=A⊕B.

这里注意：子幻方C（i，j）位于其第h行、第k列的元素是（b（h，k）-1）m2+a（i，j）（h，k=1，2，…，n）；方阵C的位于第sn+h行，第tn+k列的元素为子幻方C（s+1，t+1）的第h行、第k列的元素：

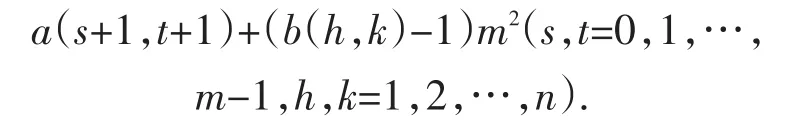
2 高阶f幻方的证明

根据以上的加法得：

定理1 设给定的m阶幻方A，n阶幻方B都是f（f=1，2，…为自然数）次幻方，则 m n阶幻方A⊕B=C亦是f次幻方.

证明 为方便起见，把幻方A中各元素（ff=1，2，…为自然数）次幂所得幻方的幻方常数记为Af，把幻方B中各元素（ff=1，2，…为自然数）次幂所得幻方的幻方常数记为Bf.

1）先证幻方是（ff=1，2，…为自然数）次幻方，以b1，b2，…，bn表示B的所关注的任一行，任一列，或任一对角线的元素，则（b1）f+（b2）f+…+（bn）f=Bf.因的元素为 b（ h，k）-1（h，k=1，2，…，n），显然，中各元素（ff=1，2，…为自然数）次幂所得幻方的对应的行，列，对角线的元素的和为

为一常数，所以幻方是（ff=1，2，…为自然数）次幻方.以m2乘的所有元素得幻方，显然幻方亦是（ff=1，2，…为自然数）次幻方.把幻方中各元素（ff=1，2，…为自然数）次幂所得幻方的幻方常数记为.为表述方便起见，以(h,k)表示的第h行，第k列元素-b（h，k）=（b（h，k）-1）m（2h，k=1，2，…，n）.

幻方所有元素加同一个a（i，j）得到C（iji，j=1，2，…，m），C（i，j）位于其第h行、第k列的元素为（h，k）+a（i，j）=（b（h，k）-1）m2+a（i，j）（h，k=1，2，…，n）；C的位于第sn+h行，第tn+k列的元素为子幻方C（s+1，t+1）的第h行、第k列的元素：a（s+1，t+1）+（h，k）=a（s+1，t+1）+（b（h，k）-1）m（2s，t=0，1，…，m-1；h，k=1，2，…，n）.

2）证明幻方C是（ff=1，2，…为自然数）次幻方.

是一常数，以Df表之.即幻方C各行的元素f方之和都等于常数Df.同理可证C的各列元素的f方之和亦等于常数Df.

C的位于由左下角至右上角方向对角线上的元素，由幻方C（1，m），C（2，m-1），…，C（m，1），的相同方向对角线上的元素所组成.C（i，m-i+1）（i=1，2，…，m）的该方向对角线上的元素f方之和为

由此C的位于由左下角至右上角方向对角线上的元素f方之和为

即幻方C的由左下角至右上角方向对角线上元素f方之和等于常数Df.同理可证C的位于由左上角至右下角方向对角线上元素f方之和等于常数Df.

也就是说幻方C中元素取f次幂仍为幻方，这个新的幻方的幻方常数是Df.由此定理得证.

推论 m阶k1次幻方与n阶k2次幻方的和是mn阶t次幻方，这里t是k1与k2中之较小者.

例 用上述幻方CH构造144阶3次幻方.

文[1]的幻方CH见图1.

图1 幻方CHFig.1Magic squre CH

根据定理1，令A=B=CH，则A⊕B=A⊕A=CH⊕CH是一个144阶3次幻方（略）.

定理2 设给定的m阶幻方A，n阶幻方B都是f（f=1，2，…为自然数）次完美幻方，则mn阶幻方A⊕B=C亦是f次完美幻方.

证明 为方便起见，使用定理1的记号，以b1，b2，…，bn表示B的所关注的任一行，任一列，任一对角线或任一泛对角线的元素，由于已有定理1，我们只须就完美性进行证明即可.

下面考虑幻方C中与由左上角至右下角对角线相同方向的泛对角线，由文[1]知，过C的元素c（sn+h，1）（s=0，1，…，m-1；h=1，2，…，n）的泛对角线.

当h=1时，该泛对角线的元素由子幻方

同向对角线上的元素所组成，这些元素f次方之和为

当h=2，3，…，n时，该泛对角线穿越子幻方

以及子幻方

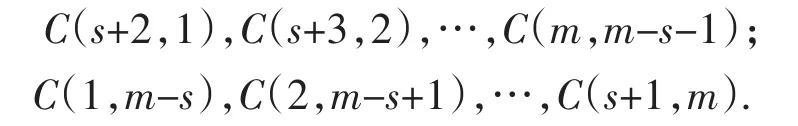
该泛对角线的元素f次幂之和为

由此证得，幻方C中任一条与由左上角至右下角对角线方向相同的泛对角线，其上的元素f次方后之和都等于常数Df.

同理可证，幻方C中任一条与由左下角至右上角对角线方向相同的泛对角线，其上的元素f次方后之和都等于常数Df.

综上所述mn阶幻方A⊕B=C亦是f（f=1，2，…为自然数）次完美幻方.

推论 m阶k1次完美幻方与n阶k2次完美幻方的和是mn阶t次完美幻方，这里t是k1与k2中之较小者.

目前，已知的较低阶f次完美幻方是32阶2次完美幻方，可以根据定理2构造出1024阶2次完美幻方.

[1]詹森.你亦可以造幻方[M].北京:科学出版社,2012:198-208.

[2]吴鹤龄.幻方及其他[M].北京:科学出版社,2004:150-153.

[3]詹森,王辉丰.关于构造高阶幻方的新方法[J].海南师范大学学报:自然科学版,2009,22(3):250-254.

责任编辑：黄 澜

Addition Method of Building High Orders f-multi Magic Square

ZHAN Sen
（Department of Computer Science,Guangdong Technical Normal University，Guangzhuo 510665，China）

The addition method that can be used to build high orders f-multi magic square was given.Two theorems were proved:Add up two f-multi magic squares and you would get another f-multi magic square;This new f-multi mag⁃ic square would be f-multi perfect magic square if they are f-multi perfect magic squares.

magic square；addition；f-multi magic square；f-multi perfect magic square

O 157.6

A

1674-4942（2012）03-0263-05

2012-05-09