函数列极限函数一致连续性的探讨

丁平仁

（山西大同大学数学与计算机科学学院，山西大同 037009）

函数列极限函数一致连续性的探讨

丁平仁

（山西大同大学数学与计算机科学学院，山西大同 037009）

在函数列收敛及一致收敛前提下探讨了极限函数的一致连续性，并且给出了函数列极限函数一致连续性的运算。

一致连续；一致收敛；一致有界

函数一致连续性是高等数学中的一个重要概念，而函数列极限函数的一致连续性一般教科书都没有涉及［1-5］。既然函数列极限函数是一个函数，我们就有必要了解它的一致连续性，下面对函数列极限函数的一致连续性作一些探讨。

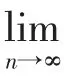
证明 由于｛fn（x）｝在I上收敛于f（x），所以f（x）在I上有定义，下面用反证法证明f（x）在I上一致连续。

假设f（x）在I上非一致连续，即

∃ε0＞0，∀δ＞0，∃x、y∈I，当|x-y|＜δ，有

|f（x）-f（y）|≥ε0，

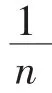
|f（x）-f（y）|≥ε0，

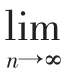
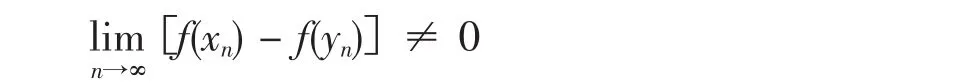
与题设条件矛盾，所以f（x）在I上一致连续。

定理2 设函数列｛fn（x）｝在有界区间I上收敛于f（x），对任意柯西数列｛xn｝⊂I，函数值数列｛f（xn）｝也是柯西数列，则f（x）在区间I上一致连续。

证明 用反证法证明f（x）在I上一致连续。假设f（x）在I上非一致连续，即

∃ε0＞0，∀δ＞0，∃x′、x″∈I，当|x′-x″|＜δ，有

|f（x′）-f（x″）|≥ε0，

则｛yn｝是柯西数列，但对任意k，有

|f（y2k-1）-f（y2k）|≥ε0，

即｛f（yn）｝不是柯西数列，与题设条件矛盾，所以f（x）在I上一致连续。

以上两个定理适用于极限函数已知以及极限函数具有某些特性的情况，对极限函数不易求得以及抽象函数列，可以通过函数列本身的特性来判别。

定理3 若函数列｛fn（x）｝在区间I上满足：

（1）｛fn（x）｝在I上一致收敛于函数f（x）；

（2）｛fn（x）｝的每一项在I上一致连续，则f（x）在区间I上一致连续。

证明 ∀ε＞0，由于｛fn（x）｝在I上一致收敛，故∃N，当n≥N时，∀x∈I，有

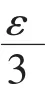
于是，∀ε＞0，∃δ＞0，∀x′、x″∈I，当|x′-x″|＜δ，有

|f（x′）-f（x″）|≤|fN（x′）-f（x′）|+

|fN（x′）-fN（x″）|+|fN（x″）-f（x″）|＜

所以f（x）在I上一致连续。

定理4 设函数列｛fn（x）｝、｛gn（x）｝在区间I上满足：

（1）｛fn（x）｝、｛gn（x）｝在I上分别一致收敛于f（x）与g（x）；

（2）｛fn（x）｝、｛gn（x）｝的每一项在I上一致连续，则f（x）±g（x）在区间I上一致连续。

证明 由定理条件及定理3，f（x）、g（x）在I上一致连续，即

∀ε＞0，∃δ＞0，∀x′、x″∈I，当|x′-x″|＜δ，有

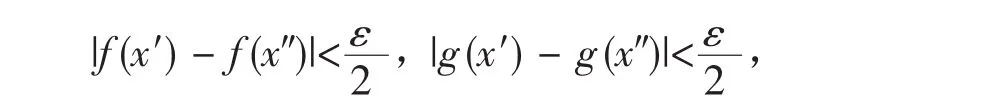
于是∀ε＞0，∃δ＞0，∀x′、x″∈I，当|x′-x″|＜δ，有

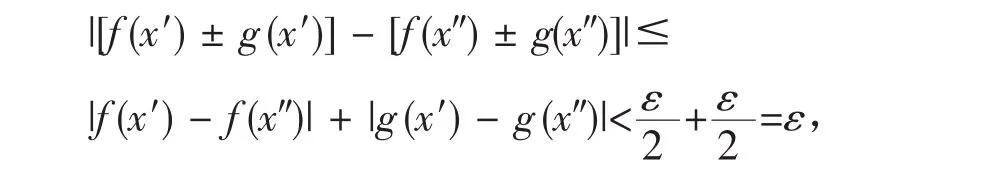
所以f（x）±g（x）在I上一致连续。

定理5 设函数列｛fn（x）｝、｛gn（x）｝在区间I上满足：

（1）｛fn（x）｝、｛gn（x）｝在I上分别一致收敛于f（x）和g（x）；

（2）｛fn（x）｝、｛gn（x）｝在I上一致有界；

（3）｛fn（x）｝、｛gn（x）｝的每一项在I上一致连续，则｛fn（x）gn（x）｝极限函数f（x）g（x）在区间I上一致连续。

证明 因为｛fn（x）｝、｛gn（x）｝在I上一致有界，即

又｛fn（x）｝、｛gn（x）｝在I上分别一致收敛于f（x）与g（x），上两式取极限，有|f（x）|≤M，|g（x）|≤M，x∈I。

由定理条件（1）、（3）及定理3，f（x）、g（x）在I上一致连续，即

∀ε＞0，∃δ＞0，∀x′、x″∈I，当|x′-x″|＜δ，有

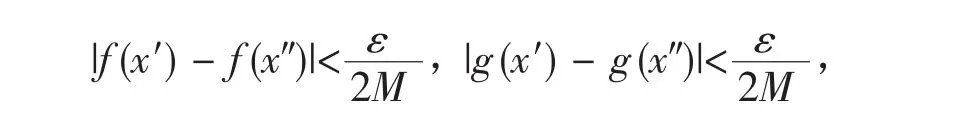
于是|［f（x′）g（x′）］-f（x″）g（x″）|≤

所以f（x）g（x）在I上一致连续。

定理6 设函数列｛fn（x）｝、｛gn（x）｝在区间I上满足：

（1）｛fn（x）｝、｛gn（x）｝在I上分别一致收敛于f（x）与g（x）；

（2）｛fn（x）｝在I上一致有界；

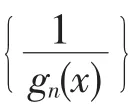
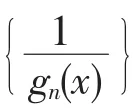
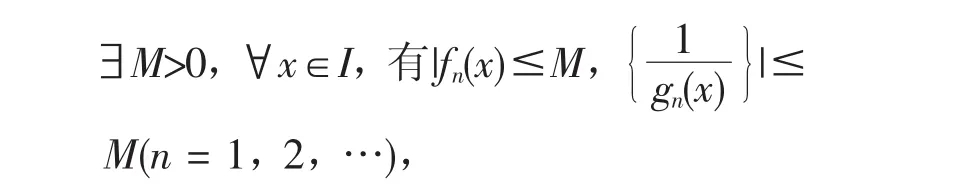
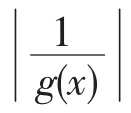
由定理条件（1）、（4）及定理3，f（x）、g（x）在I上一致连续，即

∀ε＞0，∃δ＞0，∀x′、x″∈I，当|x′-x″|＜δ，有

于是，

定理7 设函数列｛fn（u）｝在区间U上满足：

（1）｛fn（u）｝在U上一致收敛于f（u）；

（2）｛fn（u）｝的每一项在U上一致连续，又g（x）在区间X上一致连续，且

｛g（x）|x∈X｝⊂U，则｛fn［g（x）］｝极限函数f［g（x）］在区间X上一致连续。

证明 由定理条件（1）、（2）及定理3，f（u）在U上一致连续，即

∀ε＞0，∃η＞0，∀u′、u″∈U，当|u′-u″|＜η，有

|f（u′）-f（u″）|＜ε，

又g（x）在区间X上一致连续，及｛g（x）|x∈X｝⊂U，

对η＞0，∃δ＞0，∀x′、x″∈X，当|x′-x″|＜δ，有

|g（x′）-g（x″）|＜η，

于是|f［g（x′）］-f［g（x″）］|＜ε，

所以f［g（x）］在X上一致连续。

上面讨论了函数列极限函数的一致连续性，对函数项级数和函数、含参变量广义积分积分函数等可作类似讨论。

［1］同济大学数学系.高等数学［M］.6版.北京：高等教育出版社，2007.

［2］华东师范大学数学系.数学分析［M］.3版.北京：高等教育出版社，2001.

［3］徐丽.函数列一致连续和一致收敛及等度连续的关系［J］.上海电力学院学报，2007，23（3）：285-291.

［4］郑德印.一致连续与一致收敛概念的统一［J］.南都学坛，1993，13（3）：11-12.

［5］谢永红，乔玉英，杨贺菊.关于“一致”问题的探讨［J］.石家庄职业技术学院学报，2011，23（4）：44-45.

〔责任编辑 高海〕

Discussion on Uniform Continuity of the Limit Function of Function Sequence

DING Ping-ren
（School of Mathematics and Computer Science，Shanxi Datong University，Datong Shanxi，037009）

This article provides several distinguishing methods of uniform continuity of the limit function of function sequence.

uniform continuity；uniform convergence；uniform boundedness

O212.6

A

1674-0874（2012）06-0001-02

2012-08-15

丁平仁（1956-），男，山西应县人，副教授，研究方向：函数。