一类变时滞递归神经网络概周期解的存在性

郭福日，罗 芳，王振芳

（山西大同大学数学与计算机科学学院，山西大同 037009）

一类变时滞递归神经网络概周期解的存在性

郭福日，罗 芳，王振芳

（山西大同大学数学与计算机科学学院，山西大同 037009）

利用拓扑度理论，不等式技巧及Liapunov泛函方法，给出了判别变时滞静态递归神经网络概周期解存在性的充分条件。

时滞；神经网络；迭合度；概周期解

将神经元内部状态作为变量研究的递归神经网络模型已被广泛的研究［1-6］。而将神经元的外部状态作为变量研究的静态递归神经网络模型尚未被深入探讨。然而静态递归神经网络模型比局域递归神经网络模型更具有广泛的代表性，对其进行研究更具有广泛的适用性和理论价值。在文献［5］中，研究了如下静态神经网络模型：

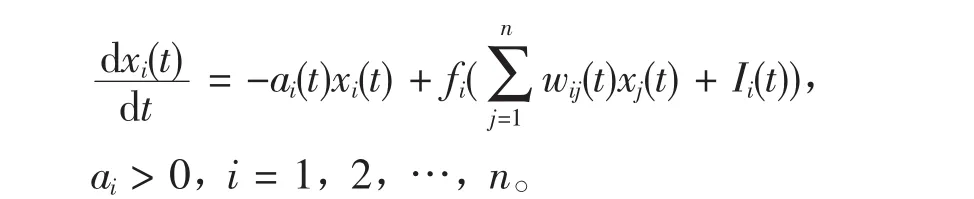
然而，在网络的运行及信号传递中，时滞是不可避免的，因此研究时滞静态神经网络是必要的且有实际意义的。

考虑如下时滞静态递归神经网络模型

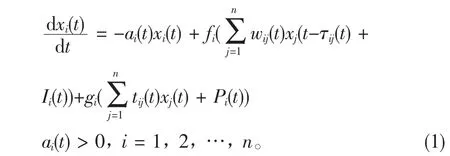
其中，wij（t），tij（t）表示连接权，fi，gi称为神经元的激活函数，τij（t）代表传输时滞，ai（t），wij（t），τij（t），tij（t），Ii（t），Pi（t）均为概周期函数。作如下的假设：

（H1）存在常数αi，βi＞0（i=1，2，…，n）使得

|fi（x）-fi（y）|≤αi|x-y|，

|gi（x）-gi（y）|≤βi|x-y|，i=1，2，…，n，

∀x，y∈R；

（H2）满足以下条件

定理1 若系统（1）满足条件（H1），（H2）则系统（1）存在唯一的概周期解x*（t）。

证明（1）概周期解的存在性，

∀X（t）=（x1（t），x2（t），…，xn（t））T∈Rn

记

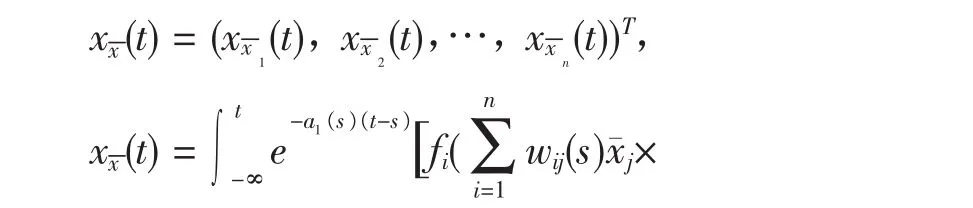
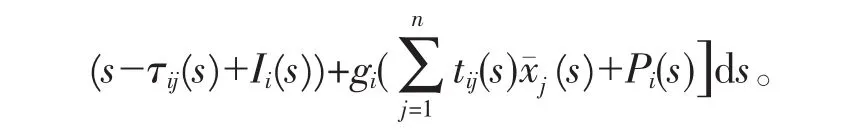
（2）概周期解的唯一性。

显然B*为B中的凸子集由（H1）可知

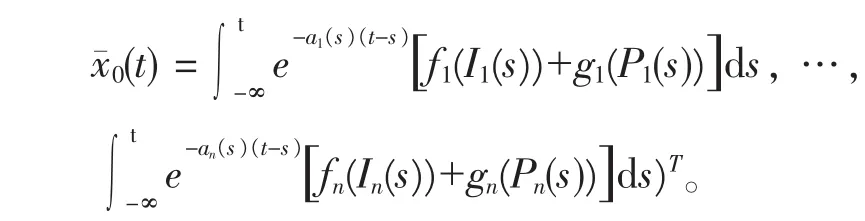
显然

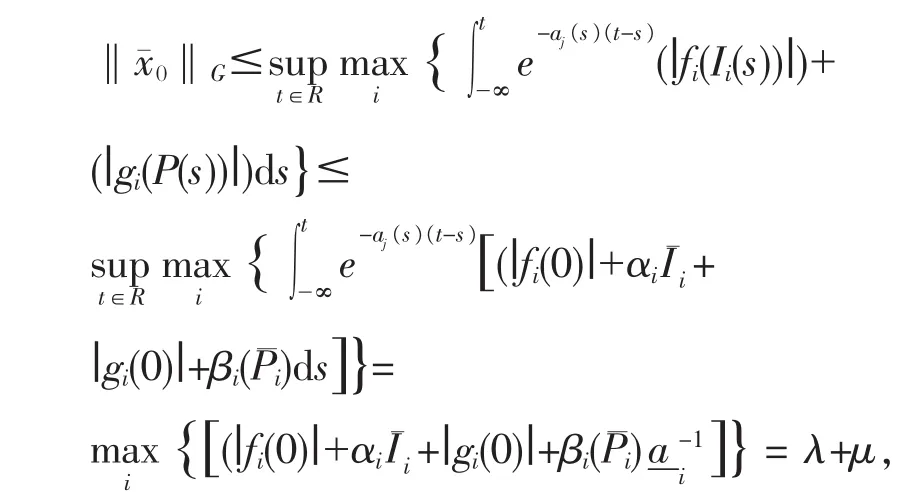
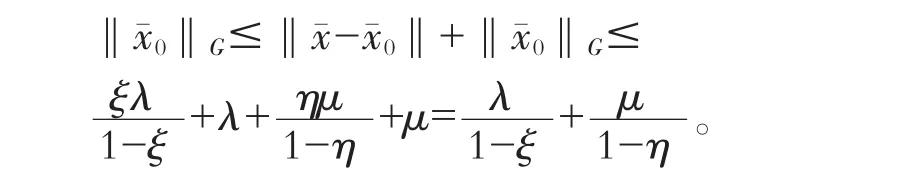
首先，证明ø为B*→B*的自映射。

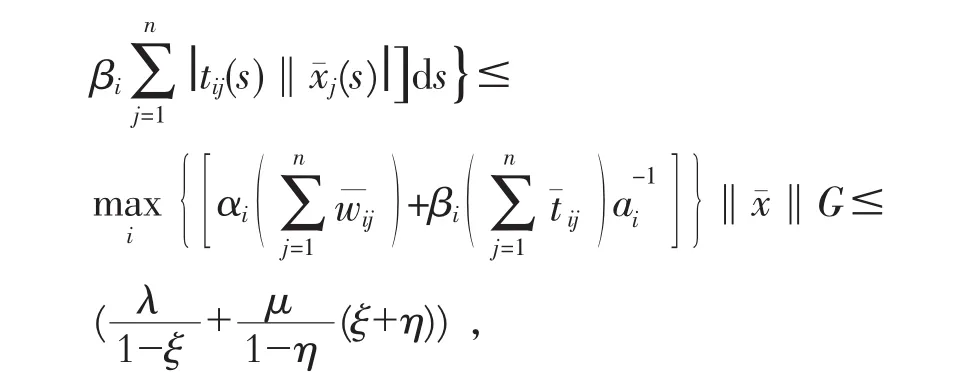
其次，证明ø为B*→B*的压缩映射。

由0＜（ξ+η）＜1知ø为B*→B*的压缩映射。由Banach不动点定理知，ø有唯一不动点x*∈B*，使得øx*=x*，所以，x*（t）是系统（1）的唯一的概周期解。

［1］王林山.时滞递归神经网络［M］.北京：科技出版社，2007.

［2］陈平安，黄立宏.Hopfield神经网络的概周期解存在性和全局吸引性［J］.数学物理学报，2001，21A（4）：505-511.

［3］李必文.具有数时滞细胞神经网络概周期解［J］.生物数学学报，2005，20（4）：372-379.

［4］廖晓昕.稳定性的理论、方法和应用［M］.武汉：华中科技大学出版社，2004.

［5］Linshan Wang，Gao Yuying.On global robust stability for interval Hopfield neural networks with time delay［J］.Ann.of Diff.Eqs.2003，19（3）：421-426.

［6］Linshan Wang，Daoyi Xu.Global asymptotic associative memory neural networks with S-type distributed delays［J］.International Journal of Systems Science，2002，33（11）：879-889.

〔责任编辑 高海〕

Existence of Almost Periodic Solutions for a Class of Static Recurrent Neural Networks with Variabled

GUO Fu-ri，LUO Fang，WANG Zheng-fang
（School of Mathematics and Computer Science，Shanxi Datong University，Datong Shanxi，037009）

By using topological degree theory，inequality techniques and Liapunov functional methods，we give the sufficient condition of existence，that the discriminant variable delay static recursive neural network almost periodic solution.

neural networks；delays；coincidence degree；almost periodic solution

O212.6

A

1674-0874（2012）06-0009-02

2012-08-15

郭福日（1980-），男，山西大同人，硕士，助教，研究方向：神经网络。