无嗅卡尔曼滤波在移动机器人定位中的应用

梅黎锦

(上海电机学院高职学院，上海 200240)

0 引言

移动机器人在运动过程中需要知道自身的位姿(位置和姿态)，这对于移动机器人的导航至关重要。众所周知，仅依靠电机码盘信息无法满足定位过程的需要，因为随着机器人移动距离的增加，码盘数据的误差也会不断增加［1］。基于特征的机器人导航的关键问题是如何有效、可靠地从传感器原始数据中获取信息［2］。激光测距仪具有高可靠性、高采样率和高测量精度等特点，被广泛应用于移动机器人的导航领域［3］。

无嗅卡尔曼滤波(unscented Kalman filter，UKF)［4］是一种非线性的最优估计器。不同于扩展卡尔曼滤波(extended Kalman filter，EKF)［5］需要线性化处理过程，UKF是基于采样原理来处理非线性问题，并且不需要服从高斯分布。通过采用合适的Sigma点采样策略，UKF较EKF能够提供更好的计算精度。本文介绍了一种新颖的移动机器人定位方法，UKF将来自电机码盘的数据和来自激光测距仪的数据进行有效融合［6］，并给出机器人位姿的最优解。该方法由数据分割、特征提取和概率定位三个主要步骤组成。

1 激光扫描数据的分割

激光扫描仪按照一定的角解析度Δφ=φn－φn－1对环境进行测量。它所提供的一帧距离像数据是离散的数据集，通常用极坐标形式描述为:

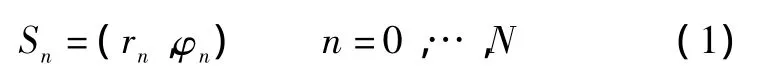
式中:(rn，φn)为第n个测量点的极坐标值;rn为在φn方向上传感器的中轴到障碍物体间的水平距离。

原始数据通常包含许多基本特征(如直线、曲线和拐角等)，因此，需要对其进行进一步分解。曲率值反映了在每一个测量点处特征的弯曲情况，属于同一特征数据的曲率值可以被认为是基本相同的。本文利用测量数据的曲率函数将聚类后的数据分割成几种独立的特征，曲率函数的具体计算方法参见参考文献［7］。

在室内环境中所采集到的激光测距传感器图像信息及其曲率函数如图1所示(图中实心圆点表示传感器原始采集信号;空心圆圈表示机器人)。从曲率函数中可以提取图像信息所含的基本形状特征。

在曲率函数中，曲率值接近零的连续区域可以认为是直线段;与直线段相反，曲率函数中表示曲线段的部分是大于某设定值的连续区域;拐角经常被认为是曲率函数上具有一定幅度的局部尖峰区域。

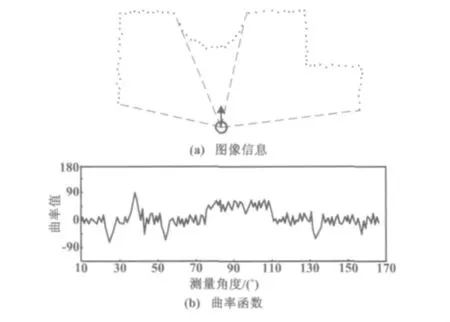
图1 采集图像及其曲率函数Fig.1 The image acquired and its curvature function

按照上述方法，从图1中所提取的直线、拐角和曲线特征如图2所示(图中实线表示传感器采集到的原始信息，大空心圆圈表示机器人，三角形表示拐角特征所在位置，连续两个正方形之间数据表示直线特征，连续两个小圆之间的数据表示曲线特征)。

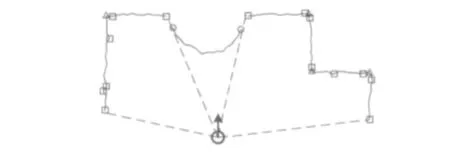
图2 提取特征示意图Fig.2 The features extracted

2 定位特征的参数提取

分割后的数据由环境中不同特征组成，如直线段、曲线和由直线段相交所构成的拐角。但是上述特征依然只是一些离散的特征点，需要更加精确地描述这些特征。

采用拟合的方法来获得特征更加精确的参数表示，提取三种相应特征参数的具体方法如下。

①直线特征

根据直线公式xcosθ+ysinθ=d，可以确定一条直线的参数(θ，d)。假设 n 个点{(ri，φi)|i=0，…，n －1}组成一条线段，则可以通过以下拟合公式计算相应的参数［8］:

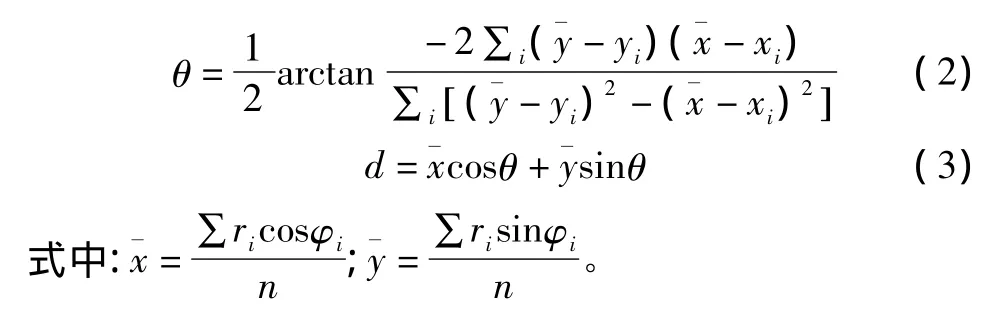
②圆弧特征

圆弧可以由以下公式定义:

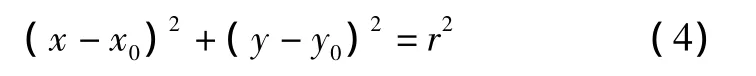
对于圆弧拟合问题，在已知属于该圆弧的点集{(xi，yi)|i=0，…，n}的情况下，计算相应圆弧参数，(x0，y0)和r分别为圆心与半径。假设获得M个测量点 p(xi，yi)，我们的目标是找到一组参数 p(x0，y0，r)复合情况下的目标函数fi，其表达式为:

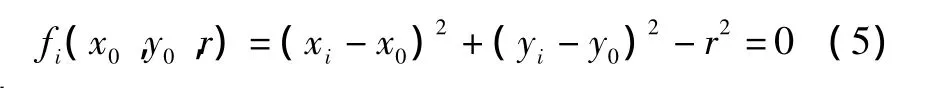
式中:i=1，…，M。

这里使用 Levenberg-Marquardt［7－9］方法求解上述非线性最小均方问题。

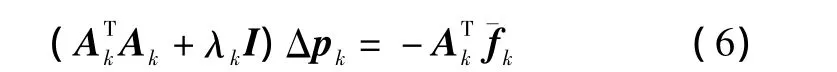
式中:A= [▽f1，▽f2，…，▽fM]T为雅克比矩阵;Δpk=pk+1－ pk，pk为第 k 次迭代所获得参数 p(x0，y0，r)的估计值。初始值p0可以通过p(xi，yi)中的任意三点，根据过三点的曲线计算公式获得。

③拐角特征

拐角特征通常是两条直线的交点，可以根据组成该拐角的直线特征计算获得。假设得到两条直线xcosθ1+ysinθ1=d1和 xcosθ2+ysinθ2=d2，这两条直线的相应交点(xc，yc)的计算公式为:

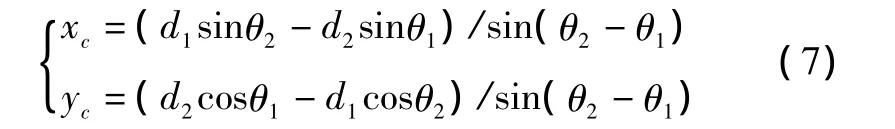
式中:(d1，θ1)和(d2，θ2)可以通过式(2)和式(3)获得。

3 移动机器人定位

为了获得更高的定位精度，本文提出了一种基于UKF的机器人位姿计算方法，通过对机器人外部环境的感知来减小定位误差。

3.1 运动与观测模型

运动模型反映了机器人的位姿向量x(k)在输入控制量 u(k)=［Δsl，Δsr］k的作用下随时间变化的过程，具体形式为:

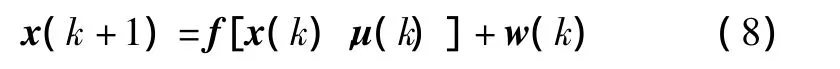
式中:w(k)～N［0，Q(k)］;f［x(k)，u(k)］为非线性状态转移方程;w(k)为系统噪声分布，具有零均值和方差Q(k)。

本文所使用的机器人具有两轮差速移动机构，其具体运动模型可以表示如下［10］:

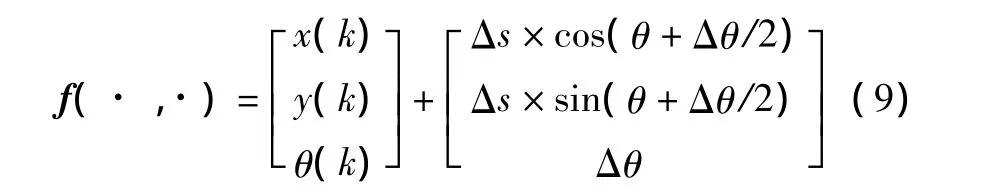
式中:Δs=(Δsr+Δsl)/2，Δθ=(Δsr－Δsl)/b;b为两驱动轮之间的宽度;控制输入 u(k)=［Δsl，Δsr］k为两轮的位移量。该位移量可以从电机码盘获得。

观测模型h［x(k)，pj］描述了传感器观测到第j个定位特征zj(k)与机器人位姿x(k)之间的关系，可以表示为:

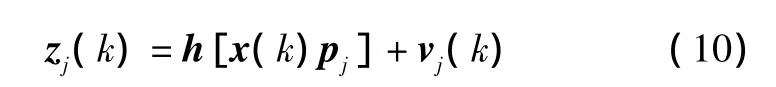
式中:vj(k)～N［0，Rj(k)］;vj(k)为测量过程中的随机噪声和模型本身的不确定性，一般假设为高斯分布N［0，Rj(k)］噪声;pj为地图上第 j个特征位置。

对于不同的传感器会有不同形式的观测方程。假设传感器(本文为激光测距仪)的观测值如式(10)所示，则在k时刻获得的第j个观测量zj(k)可采用如下观测方程表示，即:

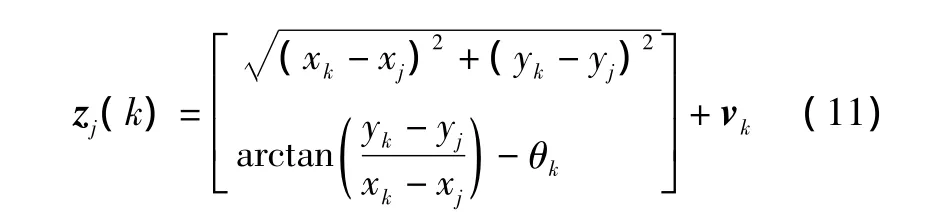
式中:pj=［xj，yj］T为探测到的第 j个特征的坐标;x(k)=［xk，yk，θk］T为机器人在时刻 k 的位姿。

3.2 融合计算

单一传感器测量结果存在一定误差，难以保证定位的准确性和可靠性。目前的传感器技术水平还很难满足自主移动机器人的要求，所以移动机器人往往同时装备多种传感器。这里我们利用UKF将来自激光测距传感器的信息与来自驱动电机码盘的信息相融合，解决了室内自然环境中移动机器人定位问题。下面给出具体的位姿计算过程。

首先，通过运动模型(9)和控制输入u(k)，可以预测机器人在下一时刻(k+1)的位姿，即:

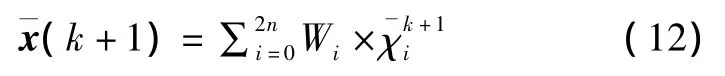
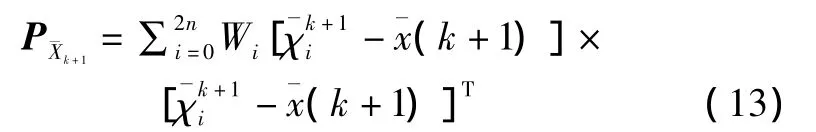
然后利用观测模型和机器人位姿的预测值，可以获得(k+1)时刻路标pj(j=1，…，M)的预测位置:

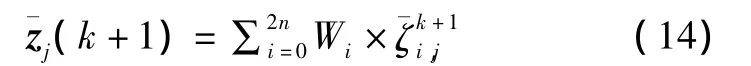
假设通过激光传感器可以获得M个路标的位置，并且根据式(14)可以获得相应的路标预测值，则路标测量值与预测值之间的误差称为新息vj，表示如下:

新息方差Sj(k+1)可以根据以下公式获得:

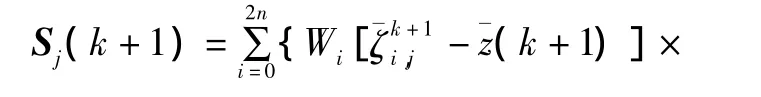
式中:Rj(k+1)为传感器测量值zj(k+1)的误差。

在每一时刻(k+1)可以获得N个路标的观测值zj(k+1)和M个路标的预测值¯zj(k+1)。为了将N个观测值与M个预测值相匹配，我们使用如下公式:

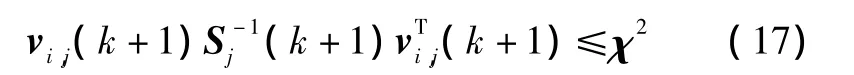
式(17)表明，当第i个观测值与第j个预测值之间的距离小于一个阈值时，就认为它们匹配。

最后，利用计算获得新息νj(k+1)更新机器人预测位姿¯x(k+1)及其方差P¯Xk+1。更新后的机器人位姿和方差为:

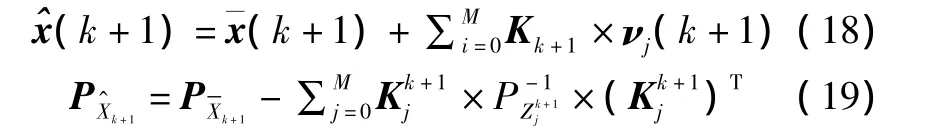
其中，Kk+1为卡尔曼滤波增益，具体计算公式如下:

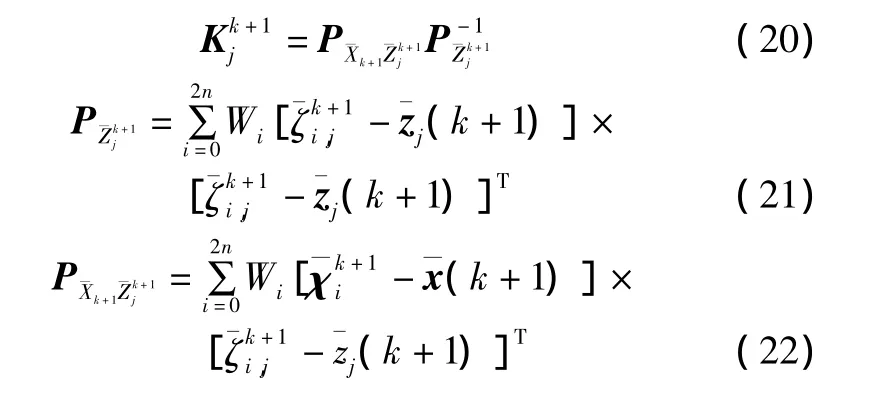
4 试验结果

试验使用美国ActiveMedia Robotics公司开发的Pioneer3移动机器人测试本文所述定位方法的性能。机器人所安装的激光传感器为德国SICK公司的LMS200型激光传感器。通过高速串行接口，可实时将测量数据传送给数据采集计算机进行进一步的数据处理。根据实际需要，本试验将激光测距仪的扫描范围设为180°，测量角度分辨率设为0.5°，扫描时间设为26 ms。这样扫描一周可以得到361个数据点。

为了说明本文所述特征提取方法以及基于该方法的机器人定位算法的有效性，我们进行了室内环境中的移动机器人定位计算试验。在机器人移动过程中，采用本文所述定位方法计算得到的机器人位置轨迹以及为了定位而提取的环境特征如图3所示。

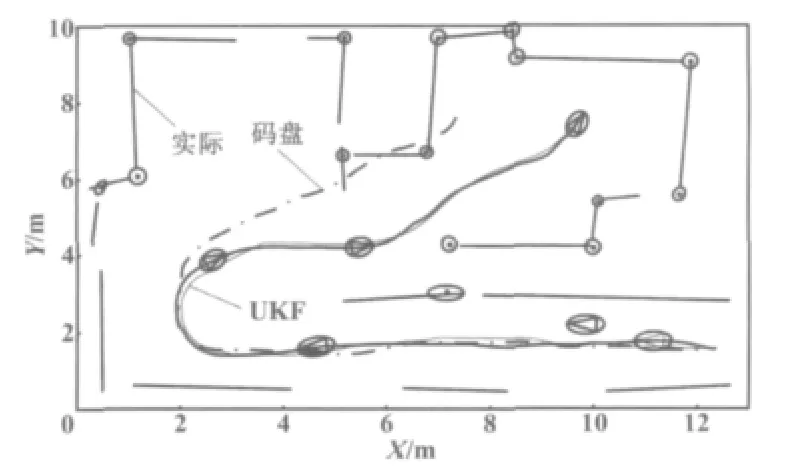
图3 机器人定位试验结果Fig.3 The experimental results of robot positioning

图3中，椭圆表示所提取特征(这里以拐角作为定位参考特征)和计算所得机器人位姿的误差;实线表示机器人的实际运动轨迹;虚线表示通过本文所述定位方法计算的轨迹;点划线表示仅依靠码盘实现的定位计算。

基于UKF数据融合的机器人定位方法计算误差如图4所示。图4中，用深色曲线分别给出了X、Y、θ三个量的结果;作为比较，用浅色曲线显示了仅依靠码盘数据计算机器人位姿的误差。试验中运动模型计算方差与传感器测量方差分别取为 R=diag(80，80，0.1)、Q=diag(20，20)，机器人位姿的初始化方差矩阵取为 P0=diag(100，100，0.05)。

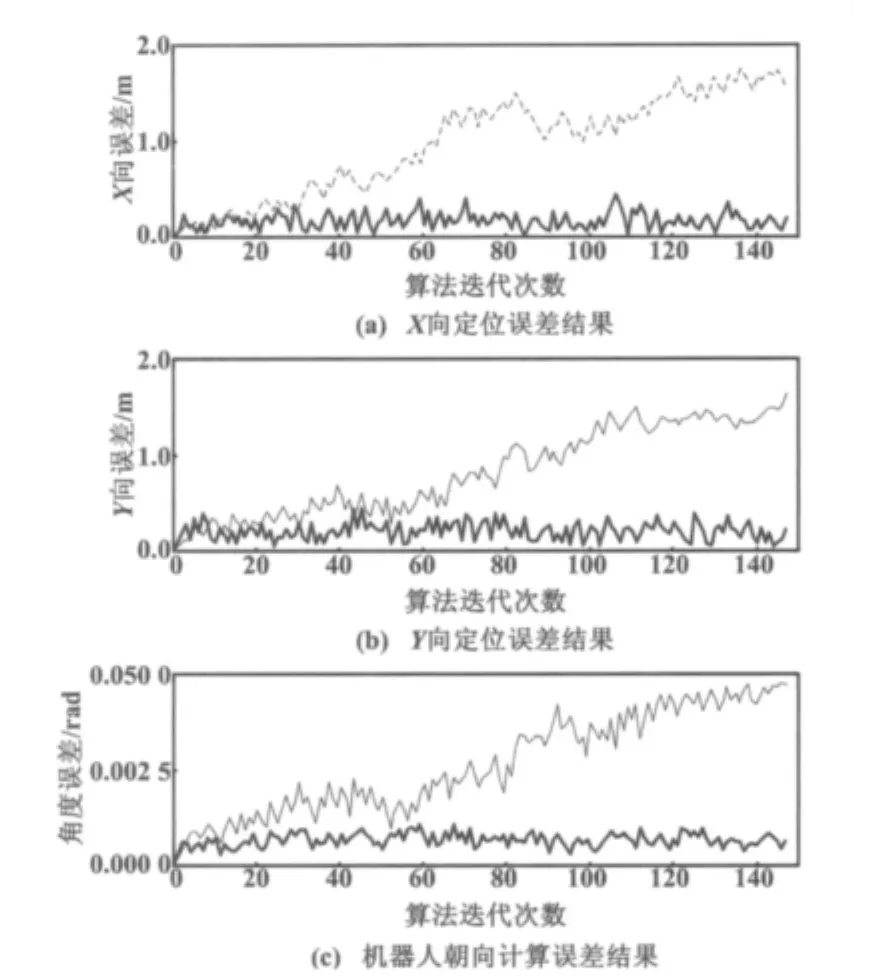
图4 机器人定位误差结果Fig.4 The error of robot positioning

从图4可以看出，起始阶段依靠码盘实现的位姿误差累积效应并不明显，所以估计的精度还是比较理想;但随着行走时间的延长误差逐渐增大，到达图示轨迹的末尾阶段误差已经非常大。采用本文所述算法计算的轨迹与理论轨迹虽然不能完全重合，但有效地抑制了误差的快速积累，明显提高了估计的精度。

5 结束语

本文首先介绍了一种针对二维激光测距传感器的特征提取方法，在此基础上提出了一种基于UKF的移动机器人定位方法。所述特征提取方法基于传感器采集图像的曲率函数。该方法可以为机器人位姿计算提供直线、拐角和曲线特征。所提取的特征信息和来自电机码盘的信息通过UKF有效地融合在一起，有效提高了机器人位姿计算的精度和鲁棒性。试验结果显示本文所述基于UKF的移动机器人定位方法是准确和有效的。

［1］李桂芝.自主移动机器人导航定位技术研究［D］.北京:北京科技大学，2005.

［2］ Nguyen V，Martinelli A，Tomatis N，et al.A comparison of line extraction algorithms using 2D laser rangefinder for indoor mobile robotics［C］//IEEE International Conference on Intelligent Robots and Systems，2005:1929 －1934.

［3］ Xiang Z Y，Liu J L.Initial localization for indoor mobile robots using a 2D laser range finder［C］//Proceeding of SPIE mobile robot XVI，2002:168－177.

［4］ Julier S J，Uhlmann J K，Durrant-Whyte H F.A new approach for filtering nonlinear systems［C］//Proceeding of American Control Conference，Seattle，WA，1995:1628 －1632.

［5］ Kalman R E.A new approach to linear filtering and prediction problems［J］.Transaction oftheASME JournalofBasic Engineering，1960，82(D):35 －45.

［6］蔡自兴，贺汉根，陈红.未知环境中移动机器人导航控制理论与方法［M］.北京:科学出版社，2009.

［7］ Knieriemen T，Puttkamer E，Roth J.Extracting lines，circular segments and clusters from radar pictures in real time for an autonomous mobile robot［C］//Proceeding of Euromicro Workshop on Real Time Systems，1991:127 －135.

［8］ Arras K O，Siegwart R.Feature extraction and scene interpretation for map based navigation and map building［C］//Proceeding of SPIE，Mobile Robotics XII，1997.

［9］ Nash J C.Compact numerical methods for computers:linear algebra and function minimization［M］.New York:Halsted press，1979.

［10］Siegwart R，Nourbakhsh I R.Introduction to autonomous mobile robots［M］.Boston:MIT press，2004.