一类图的列表强边染色

黄会芸

（南京化工职业技术学院，江苏南京 210048）

一类图的列表强边染色

黄会芸

（南京化工职业技术学院，江苏南京 210048）

给出了列表强边染色的定义，证明了若G为d（x）＋d（y）≤5，则强边选择数Sχ′l（G）≤6.

染色；强边染色；强边色数；列表强边染色；强边选择数

1 基本概念和主要结论

仅考虑有限、无向、无环但可以有平行边的图.用G（V，E）来表示图，其中V表示图G的顶点集，E表示图G的边集.图G的一个k－边正常染色是指一个映射φ：E（G）→｛1，2，…，k｝，若对任何2个相邻的边e和e′，均有φ（e）＝φ（e′），简称为图G的一个k－边染色或称该图是k－边可染的，最小的整数k称为G的边色数，记为χ′（G）.

图G的k－强边染色是正常k－边染色，使得没有相邻于具有相同颜色的2条边.若图G存在k－强边染色，则称图G是k－强边可染的.图G的强边色数是使得G是k－强边可染的最小的整数k，记为sχ′（G）.图G的部分强边着色是指一个满足上述条件的着色，除了G的某些边未被着色.

文献［1］中提出一个公开问题：如果G是二部图，图中的任意一条边xy∈E（G），那么d（x）＋d（y）≤5.文献［2］中证明若d（x）＋d（y）≤5，则sχ′（G）≤6.

给G的每条边e分配一个颜色列表L（e），称G是L－强边染色的是指对每条边e，都可从其对应列表中L（e）找到一种染色f（e）∈L（e），使得f是G的一个强边染色.如果每条边列表长度都相同，此时强边着色数（或强边选择数）定义为满足下面条件的最小的正整数k，使对G的任一边e，只要当｜L（e）｜≥k时，G都是L强边可染的.设L为G的任意一个边列表分配，G的部分L－强边染色是部分强边染色f使得对于任意e∈E⊆E（G），有f（e）∈L（e）.

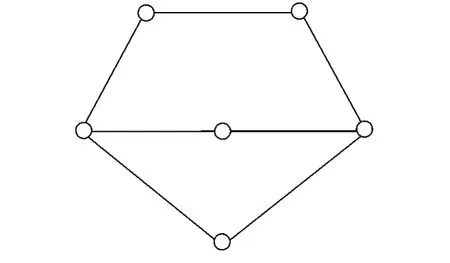
图1 H0

文献［3］中得到如下结论：当Δ（G）≤3且δ（G）≤2，则）≤10；若G为3正则图，当g（G）＝3时≤10；若G为3正则图，当g（G）≥4时

笔者将证明：除了图H0的列表强边色数等于7以外，当图的最大边度数小于等于5时，列表强边色数小于等于6.其中H0的构造如下：给定一个5圈，再增加1个顶点，将这个顶点与5圈的2个不相邻的顶点相连.可以看出H0有7条边，任意2条边之间的距离不超过2（如图1所示），从而有＝7.即证明：

定理1 给定图G，G不同构于H0，若对图G的任一条边x y，满足d（x）＋d（y）≤5，则当二度点相邻时，有≤6；当二度点不相邻时，有≤7.

2 对图的边进行排序

文献［4］利用贪心算法构造3正则图的一个部分强边着色并介绍了图的边排序的方法.笔者也将借用这种方法，给图进行边排序后，再利用贪心算法得到一个部分强边着色.

S是V（G）的顶点子集，顶点v∈V（G），dS（v）表示v到S的距离，定义为是V（G）的顶点子集，I表示从V（G）中的一个点到的S最大距离.设Di＝｛v∈V（G）｜d（v，S）＝i｝（i＝0，1，…，I）.定义一个从E（G）到［0，I］的映射dS如下：对任意一条边e∈E（G），dS（e）＝min｛i｜e∩Di≠Ø，0≤i≤I｝.S是V（G）的顶点子集，R＝（ek1，ek2，…，ekm）是图G的一个边序列.对任意2正整数i，j∈［1，m］，如果ki≤kj意味着dS（eki）≥dS（ekj），就称图G的边序列R关于映射dS是可比较的.

设E（G）中的任一条边e，E（G）的强领域N（e）是E（G）中与e的距离小于等于2的边集合.令f为图G的部分L－强边着色，对于未染色边e，E（G）为部分强边染色边集.使用F（e）表示的禁用颜色集合，F（e）＝｛f（e′）｜1≤dG（e，e′）≤2，e′∈E′｝.

Hall定理 设A1，A2，…，Am是集合S的m个子集，子集族A＝｛A1，A2，…，Am｝的一个相异代表系SDR是指S的一个子集合｛a1，a2，…，am｝满足：（ⅰ）ai∈Ai，i∈｛1，…，m｝；（ⅱ）对于任意i≠j，有ai≠aj.子集族A存在SDR当且仅当对于任意子集J⊆｛1，…，m｝有｜∪i∈jAi｜≥｜J｜.

引理1 设G是一个连通图，当图的最大边度数小于等于5，L为G的任意一个边列表分配，设对任意一条边e，｜L（e）｜＝6，S是V（G）的任意顶点子集，R是图G的关于映射dS的可比较的边序列，除了满足dS（e）＝0的边外，利用贪心算法对边序列R进行着色，即可产生图G的一个部分强边着色.

证明 如果e是满足dS（e）≥0的一条边，那么一定存在另一条边e′，e和e′有一公共的端点，并且dS（e′）≤dS（e）.设x是e和e′的公共端点，y是e′的另一端点，当利用贪心算法对e边着色时，与y关联的边还没着色.设L为G的任意边列表分配，定义e的禁用颜色集合F（e）.从图的结构可知｜F（e）｜≤5，即从｜L（e）｜＝6的列表中总可以挑出1种颜色给边e，使边e进行正常的L－强边着色.

3 d（x）＋d（y）≤5图的强边选择数

3.1 树的列表强边染色

定理2 若G是树，则sχ′l（T）＝sχ′（T）＝σ（G

证明 设A为G中度为1的顶点的集合，设uv为V（G）－A所展开的树图的一条边，令u在T的度为1，任取ω∈A，使uw∈E（G）.设L为G的任意一个边列表分配，使得对任意e∈E（G），有｜L（e）｜＝σ（G）.假设对树G－ω命题成立，即对G－ω每条边均能从长度为σ（G－ω）的列表中选取1种颜色来上色.对于未着色的边uw∈E（G）有最多dG－w（u）＋dG－w（v）＜dG（u）＋dG（v）－1＜σ（G）种禁用色，所以对于uω从它的长度为σ（G）的列表中存在至少1种未用的颜色分配给uω.

3.2 圈的列表强边染色

定理3 设Cn是长度为n的圈，则

证明 L为G的任意一个边列表分配，f为G的L－强边染色.对于任意未染色边e都定义一个可利用颜色列表L′（e）＝L（e）＼F（e），使得G中任意边e，均有｜L（e）｜＝3.

设图G的6圈为C＝v1v2v3v4v5v6，令e1＝v1v2，e2＝v2v3，e3＝v3v4，e4＝v4v5，e5＝v5v6，e6＝v6v1.

情形1 若L（e1）∩L（e4）＝Ø且L（e2）∩L（e5）＝Ø且L（e3）∩L（e6）＝Ø.令子集族e＝｛e1e2e3e4e5e6｝，对任意子集J⊆｛1，2，3，4，5，6｝，都有｜UL′（ei）｜≥｜J｜，故子集族e存在SDR，即G是L－强边可染的.

情形2 若L（e1）∩L（e4）≠Ø或L（e2）∩L（e5）≠Ø或L（e3）∩L（e6）≠Ø.设f为G的L－强边染色.不妨令f（e1）＝f（e4）＝a∈L（e1）∩L（e4）.给e2，e3，e5的颜色分别为b，c，d.对e6而言，若L（e6）≠｛a，b，d｝，则命题成立.若L（e6）＝｛a，b，d｝，考虑e5，若L（e5）≠｛a，c，d｝则将e5换色，命题成立.假设L（e5）＝｛a，c，d｝，再考虑e3，若L（e3）≠｛a，b，c｝则将e3换色，命题成立.若L（e3）＝｛a，b，c｝，有f（e3）＝f（e6）＝b，f（e1）＝f（e4）＝a，则e2，e5可正常染色，命题成立.

定理4 设Cn是长度为n的圈，则

由定理3得Sχ′l（C6）＝3.下证当n≥6且n≠3k时

设圈Cn＝v1v2v3v4v5v6…vn，ei＝vivi＋1，i＝1，…，n－i，en＝vnv1.设L为G的任意一个边列表分配.f为G的L－强边染色.对于任意未染色边e都定义一个可利用颜色列表L′（e）＝L（e）＼F（e）.

情形1 L（e1）∩L（e4）≠Ø.不妨令f（e1）＝f（e4）＝a∈L（e1）∩L（e4）.从e2开始一直到en依次着色，可以看出｜L′（e2）｜≥3，｜L′（e3）｜≥2，｜L′（e5）｜≥2，｜L′（e6）｜≥2，…，｜L′（en－1）｜≥2，｜L′（en）｜≥1，即｜L（e）｜＝4，可以得到L－强边染色.

情形2 L（e1）∩L（e4）＝Ø，先对e5从开始一直到en依次着色，｜L（e）｜＝4，可以得到L－强边染色.对于边e1e2e3e4，｜L′（e1）｜≥2，｜L′（e2）｜≥3，｜L′（e3）｜≥3，｜L′（e4）｜≥2，由L（e1）∩L（e4）＝Ø，则｜L′（e1）∪L′（e4）｜≥4，对于任意子集J⊆｛1，2，3，4｝都有｜∪L′（ei）｜≥｜J｜（i＝1，2，3，4），故L′存在SDR，根据Hall定理用｜L（e）｜＝4，就可以得到L－强边染色.

假设G是连通图，若Δ（G）＝4，则G同构于k1，4，显然）＝4；若Δ（G）＝1，则.下面分别证明Δ（G）＝2，Δ（G）＝3的情形，定理1的证明由下面一系列的定理组成.

3.3 Δ（G）＝2的图的列表强边染色

定理5 设Pn是n个顶点的路，则

3.4 Δ（G）＝3的图的列表强边染色

证明 设v0是度为1的顶点，e0是和v0关联的边.由图G的结构可知，令S＝｛v0｝，由引理1，除e0外所有边是L－强边可染的.由于｜N（e0）｜≤4，因此边e0也可正常着色.从而，≤5≤6，即命题成立.

下面假定图G没有度为1的顶点.

定理7 如果图g（G）＝2或3，那么Sχ′l（G）≤6.

证明 设S是由图G中最小圈的顶点组成的集合.首先利用贪心算法对G中所有满足dS（e）≥0的边进行着色.当g（G）＝2时，｜L′（e0）｜≥3，｜L′（e1）｜≥5，｜L′（e2）｜≥5，对于任意子集J⊆｛0，1，2｝都有｜UL′（ei）｜≥｜J｜（i＝0，1，2），故L′存在SDR，根据Hall定理用｜L（e）｜＝6就可以得到L－强边染色.同理，当g（G）＝3时，｜L′（e0）｜≥3，｜L′（e1）｜≥5，｜L′（e2）｜≥6，｜L′（e3）｜≥5，故L′存在SDR，根据Hall定理，Sχ′l（G）≤6，即命题成立.

定理8 如果图g（G）＝4，那么Sχ′l（G）≤6.

证明 设L是图G的任意一个边列表分配，使得对任意e∈E（G），有｜L（e）｜＝6.设Ø为G的部分L－强边染色，对于任意未染色边e都定义一个可利用颜色列表L′（e）＝L（e）＼F（e）.当｜E（G）≤6｜时，显然命题成立.假设｜E（G）｜＞6，设图G的4－圈为C＝v1v2v3v4，并设S＝V（C）.如果在C中至多有1个3度点，首先利用贪心算法对G中所有满足dS（e）≥0的边进行着色，那么｜L′（e0）｜≥3，｜L′（e1）｜≥5，｜L′（e2）｜≥6，｜L′（e3）｜≥6，｜L′（e4）｜≥5，故L′存在SDR，根据Hall定理用｜L（e）｜＝6，就可以得到L－强边染色.

下面考虑C中恰好有2个不相邻的3度点的情形.

不妨设d（v1）＝d（v3）＝3，设与v1和v3相邻的点分别为u1和u3，令e1＝v1v2，e2＝v2v3，e3＝v3v4，e4＝v4v1，f1＝v1u1，f3＝v3u3.如果u1＝u3，那么G与K2，3同构，显然Sχ′l（K2，3）≤6.假设u1≠u3，如果u1u3∈E（G），那么G与H0同构.因此，假设u1u3∉E（G），设u1的另一邻点是ω1，u3的另一邻点是ω3.首先利用贪心算法对G中所有满足dS（e）≥0的边进行着色.下面将Ø扩展成整个图的L－强边着色.

情形1 若L′（f1）∩L′（f3）≠Ø，则可令Ø（f1）＝Ø（f3）∈L′（f1）∩L′（f3），此时可看出，｜L′（ei）｜≥4（i＝1，2，3，4），所以可以从L′（ei）中挑出1种颜色给每条边着色，从而得到图G的｜L（e）｜＝6的L－强边着色.

情形2 若L′（f1）∩L′（f3）＝Ø，对于任意子集J⊆｛i，j｝（i＝1，2，3；j＝1，3）都有｜∪L′（ei）∪L′（fj）｜≥｜J｜，则L′＝｛L′（e）｜e为未染色边｝存在SDR，那么Ø扩展到G.

证明 设C＝v1v2v3v4v5v1是图G的一个5－圈，并设S＝v（C）.设Ø为G的部分L－强边染色，下面将Ø扩展到G.对于任意未染色边e都定义一个可利用颜色列表L′（e）.如果在C中至多有1个3度点，首先利用贪心算法对G中所有满足dS（e）≥0的边进行着色，那么｜L′（e0）｜≥3，｜L′（e1）｜≥6，｜L′（e2）｜≥5，｜L′（e3）｜≥5，｜L′（e4）｜≥6，｜L′（e5）｜≥6，对于任意子集J⊆｛0，1，2，3，4，5｝都有｜∪L′（ei）｜≥｜J｜（i＝0，1，2，3，4，5），故L′存在SDR，根据Hall定理用｜L（e）｜＝6，就可以得到L－强边染色.

下面考虑C中恰好有2个不相邻的3度点的情形.

图2 图G围长为5

不妨设d（v1）＝d（v3）＝3，设与v1和v3相邻的点分别为u1和u3，令e1＝v1v2，e2＝v2v3，e3＝v3v4，e4＝v4v5，e5＝v5v1，f1＝v1u1，f3＝v3u3，由于G没有4－圈，因此必有u1≠u3.如果u1u3∈E（G），如图2所示，先用｜L（e）｜＝6对e1e2e3e4e5进行L－强边着色.对于剩下3条边f1，f3，t1，｜L′（f1）｜≥2，｜L′（f2）｜≥2，｜L′（t1）｜≥2.又因为F（f3）＝｛e1e2e3e4｝，F（f1）＝｛e1e2e4e5｝，F（t1）＝｛e1e2e3e5｝，｜∪L′（f1）∪L′（f2）∪L′（t1）｜≥3，所以L′存在SDR，根据Hall定理用｜L（e）｜＝6，就可以得到L－强边染色.现在考虑u1u3∉E（G），设u1的另一邻点是ω1，u3的另一邻点是ω3.t1＝u1ω1，t3＝u3ω3，首先利用贪心算法对G中所有满足dS（e）≥0的边进行着色.若L′（f1）∩L′（f3）≠Ø，则可令Ø（f1）＝Ø（f3）∈L′（f1）∩L′（f3），此时可看出｜L′（ei）｜≥4（i＝1，2，3，5），｜L′（e4）｜≥5，这样可以按照边的次序e3e2e1e5e4，从每条边ei的L′（ei）中选取1种颜色给这5条边着色，从而将Ø扩充成整个图G的L－强边着色.若L′（f1）∩L′（f3）＝Ø，则对于未着色的7条边，｜L′（e4）｜＝6（i＝1，2，3，5），｜L′（ei）｜≥5（i＝1，2，3，5），｜L′（fi）｜≥3（i＝1，3）.（），｛，｝（，，，，；，），

情形1∪L′f3｜＝7对于任意子集J⊆i j i＝1 2 3 4 5 j＝1 3都有｜∪L′（ei）∪L′（fj）｜≥｜J｜，则L′＝｛L′（e）｜e为未染色边｝存在SDR，那么Ø扩展到G.

定理10 如果图g（G）＝6，那么Sχ′l（G）≤6.

证明 设C＝v1v2v3v4v5v6v1是图G的一个6－圈，并设S＝v（C）.首先利用贪心算法对G中所有满足dS（e）≥0的边进行着色.设Ø为G的部分L－强边染色，那么｜L′（ei）｜≥3（i＝1，2，3，4，5，6）.根据定理3知可以将Ø扩展到G.

定理11 如果G有2个相邻的度为2的点，且g（G）≥7，那么Sχ′l（G）≤6.

图3 图G围长至少为7

证明 由定理7，8，9，10，可假设G的围长至少是7.设v1，v2是2个相邻的度为2的点，如图3所示.设与v1，v2相邻的点分别为u1，u2，设e1＝v1v2，f1＝v1u1，f2＝v2u2，设N（u1）＝｛v1w1w2｝，N（u2）＝｛v2w3w4｝.由于G中没有圈长小于6的圈，也没有度为1的点，因此w1w2w3w4是度为2的4个不同点，g1＝u1w1，g2＝u2w2，g3＝u2w3，g4＝u2w4.设L为G的任意一个边列表分配，对于任意未染色的边e定义一个可利用颜色列表L′（e），Ø为G的部分L－强边染色，令S＝｛v1，v2，u1，u2｝.利用贪心算法对满足dS（e）≥0的边进行部分L－强边染色，此时｜L′（e1）｜≥6，｜L′（fi）｜≥4，｜L′（gi）｜≥2.，｛，，｝（；，；，，，）（）

情形1 ≥7对于任意子集J⊆i j k i＝1 j＝1 2 k＝1 2 3 4都有｜∪L′ei∪L′（fj）∪L′（gk）｜≥｜J｜，则L′＝｛L′（e）｜e为未染色边｝存在SDR，那么Ø扩展到G.

图4 图G的围长至少为8

证明 假定G是连通图并且没有1度点.设v0是度为2的点且N（v0）＝｛u1u2｝，如图4所示.设L为G的任意一个边列表分配，对于任意未染色的边e定义一个可利用颜色列表L′（e）.设Ø为G的部分L－强边染色，令S＝｛v0｝.利用贪心算法对满足dS（e）≥0的边进行部分L－强边染色.此时｜L′（e1）｜≥1，｜L′（e2）｜≥1，由于已着色，下面根据fi着色的色类可分为2，3，4这3类：

情形1 当｜Ø（fi）｜≤3，此时｜L′（e1）｜≥2，｜L′（e2）｜≥2，则e1e2可正常着色，从而Ø扩展到G.

情形2 当｜Ø（fi）｜＝4，此时｜L′（e1）｜≥1，｜L′（e2）｜≥1，考虑边g1g2的着色.

情形2.1 当Ø（g1）＝Ø（g2），此时｜L′（e1）｜≥2，｜L′（e2）｜≥2，则e1e2可正常着色.

情形2.2 当Ø（g1）＝Ø（f3）或Ø（g1）＝Ø（f4）或Ø（g2）＝Ø（f3）或Ø（g2）＝Ø（f4），此时｜L′（e1）｜≥2，｜L′（e2）｜≥2，则e1e2可正常着色.

情形2.3 当Ø（g1）≠Ø（g2）且Ø（g1）≠Ø（f3）且Ø（g1）≠Ø（f4），不妨设Ø（f1）＝a，Ø（f2）＝b，Ø（f3）＝c，Ø（f4）＝d，Ø（g1）＝x，Ø（g2）＝y，Ø（g3）＝z，Ø（g4）＝m，L1＝｛a，b，c，d，x，y），L2＝｛a，b，c，d，z，m｝.

情形2.3.1 若｜L（e1）∩L1｜≤5或｜L（e2）∩L2｜≤5，则e1e2可正常着色.

情形2.3.2 若｜L（e1）∩L1｜＝6且｜L（e2）∩L2｜＝6，不妨令L（e1）＝｛a，b，c，d，x，y，A｝，L（e2）＝｛a，b，c，d，z，m，B｝.

情形2.3.2.1 若A≠B，令Ø（e1）＝A，Ø（e2）＝B，则e1e2可正常着色.

情形2.3.2.2 若A＝B，则对g1进行换色.由于｜L′（g1）｜≥3，对g1而言，除色x外，还有另外2种色α，β可选，如将Ø（g1）＝x换为Ø（g1）＝α.若α≠Ø（f1）＝a且α≠Ø（f2）＝b，则可令Ø（e1）＝e，Ø（e2）＝A即可完成着色.若α＝Ø（f1）＝a且α＝Ø（f2）＝b，则f1随之换色，令Ø（f1）＝a，此时可令Ø（e1）＝A，Ø（e2）＝a即可完成着色.

［1］ FAUDREE R J，SCHELP R H，GYARFAS A，et al.The Strong Chromatic Index of Graphs［J］.Ars Combinatoria，1990，29B：205－211.

［2］ WU Jian－zhuan.The Strong Chromatic Index of a Class of Graphs［J］.Discrete Mathematics，2008，308：6 254－6 261.

［3］ 朱海洋.Delta（G）＝3的图的列表强边染色［J］.山东理工大学学报，2008，22：54－58.

［4］ ERDOS P.Problems and Results in Combinatorial Analysis and Graph Theory［J］.Discrete Mathematics，1988，72：81－92.

List Strong Edge Coloring of Some Graphs

HUANG Hui－yun
（Nanjing Colleng of Chemical Technology，Nanjing 210048，China）

List strong edge coloring is defined.It is proved that if G is a graph with d（x）＋d（y）≤5，then

coloring；strong edge coloring；strong edge chromatic number；list strong edge coloring；strong edge choice number

book=25,ebook=129

O157.5

A

10.3969／j.issn.1007－2985.2012.04.006

（责任编辑 向阳洁）

1007－2985（2012）04－0025－06

2012－04－11

黄会芸（1979－），女，江西高安人，南京化工职业技术学院基础部讲师，硕士，主要从事数学教学研究.