基于近似模型的两级集成系统协同优化方法

蒋 平 匡 玲 邵新宇 肖 蜜

华中科技大学数字制造装备与技术国家重点实验室，武汉，430074

0 引言

复杂工程系统（如飞机、船舶、汽车、机械装备等）的设计通常涵盖多个相互耦合的学科，为了对多学科耦合进行有效处理，以获得最优的系统设计方案，Sobiesczanski－Sobieski［1］提出了多学科设计优化（multidisciplinary design optimization，MDO）方法。

MDO方法也称MDO策略，是当前MDO领域的研究热点。MDO方法按照是否对系统进行分级处理，可分为单级MDO方法和多级MDO方法两大类。相比单级 MDO方法，多级MDO方法更符合复杂工程系统设计的组织模式，利于进行学科间的并行设计和分布式计算。常用的多级MDO方法主要有：协同优化（collaborative optimization，CO）方法、并行子空间优化（concurrent subspace optimization，CSSO）方法、分层目标传递（analytical target cascading，ATC）方法和两级集成系统综合（bi－level integrated system synthesis，BLISS）方法。其中，BLISS中的BLISS2000被认为是目前全局优化性能最强的多级MDO方法［2］。但BLISS2000方法仍然存在比较大的改进空间，其中，作为子系统级影响系统级的权值系数w的数学意义并不明确，而且若优化问题存在大量耦合，将它作为系统级设计变量，那么系统级设计变量的维数将大大增加，导致搜索难度和计算量加大。CO方法虽然从结构形式上较好地解决了复杂工程系统设计的组织复杂性问题，但容易出现难于收敛和陷入局部收敛的现象。为此，结合BLISS2000和CO特点的两级集成系统协同优化（bi－level integrated system collaborative optimization，BLISCO）方法被提出［3］，从组织形式和协调分解方面更好地解决了大规模多学科耦合问题。

在复杂工程系统的多学科设计优化中，往往涉及众多高精度的仿真分析模型，如结构有限元分析模型、气动分析模型，以及计算流体动力学分析模型等，这使得计算成本大大增加；同时，在学科仿真分析中，不可避免地会产生一些数值噪声，这将降低求解算法的收敛速度，甚至导致无法获得全局最优解。因此，有必要在设计过程中引入近似模型来代替高精度的仿真分析模型，降低反复调用高精确仿真分析模型的计算成本，缩短设计周期，平滑数值噪声，获得整体最优的设计方案。

基于以上分析，本文提出了一种BLISCO与近似模型技术相结合的MDO方法，通过在BLISCO方法中引入近似模型来降低计算复杂度，加快算法收敛速度，避免数值噪声，提高设计优化效率。并且通过具体的算例，验证了本文所提出方法的有效性和可行性。

1 基于近似模型的BLISCO方法

1.1 BLISCO方法

BLISCO是一种两级优化方法，分为系统级优化和子系统级优化。系统级优化负责协调子系统之间的差异，子系统级优化负责最小化耦合输出状态变量对系统目标函数的综合影响。BLISCO方法保留了CO方法的协同机制，而用子系统耦合输出状态变量的加权和代替子系统一致性约束作为其优化的目标函数。BLISCO方法在形式上更类似于BLISS2000方法，不同的是BLISCO方法通过严格的推导，明确了w的数学定义，从而在系统级消除了w变量，降低了系统级设计变量的维数，不需要进行包含系统级优化和子系统级优化的系统迭代过程。

对涉及N个子系统的多学科设计优化问题，采用BLISCO方法所得到的数学模型如下［4］。

（1）子系统级优化。在系统级给定 ｛zshare，zy｝的条件下，第i个子系统优化问题可表述为

其中，zi是系统级设计变量，包括｛zshare，zy｝，zshare为系统级共享设计变量，zy为对应子系统耦合状态变量的系统级耦合设计变量；yi，j是子系统i的第j个耦合状态变量；xi是子系统的局部设计变量；D（f，）是系统级目标函数对初始耦合设计变量的导数；gi和hi分别表示第i个子系统的不等式约束和等式约束。如果第i个子系统的状态变量包含系统级目标f，那么该子系统的目标函数就是系统级目标函数，这体现了该子系统对系统级目标函数的全部影响。D（f，）可通过两种方式获得：当系统级目标函数为耦合设计变量的显函数时，可通过解析法直接获得导数信息而不需要进行子系统分析；当系统级目标函数为耦合设计变量的隐函数时，可采用先通过子系统优化得到约束对应的拉格朗日乘子，然后进行最优灵敏度分析的方法获得导数信息［5］。

（2）系统级优化。即

其中，y＊为子系统优化后获得的耦合状态变量值；C为耦合设计变量和耦合状态变量之间的一致性约束；gs和hs分别为系统级的不等式约束和等式约束。

1.2 近似模型

在设计优化过程中，不可避免地要对设计空间进行有效探索。复杂系统的MDO问题，存在着计算复杂、组织复杂、模型复杂以及信息交换复杂等问题，直接将单学科设计优化中常用的设计空间搜索优化算法应用于多学科分析中是不切实际的［6］。

近似模型技术就是用现有的简单模型拟合原始的复杂设计空间，可以减少设计优化过程中的计算次数、预计输入输出参数之间的关系，避免算法陷入局部最优。同时，近似模型技术与优化算法的不同组合，还可以提供新的优化问题求解方法。近似模型技术作为学科分析和优化算法之间的接口，已得到了广泛的应用［7－8］。目前常用的近似模型包括响应面模型、径向基神经网络模型、泰勒序列逼近模型以及Kriging模型［9］。构建近似模型的一般流程如图1所示。

图1 构建近似模型的一般流程图

1.3 近似模型与BLISCO方法的结合

本文将近似模型与BLISCO方法相结合，提出了基于近似模型技术的BLISCO方法，算法结构如图2所示。

图2 基于近似模型的BLISCO方法基本结构

在图2所示算法结构中，包括子系统级优化、子系统级优化、子系统级分析及近似模型的建立。zshare是系统级共享设计变量；zy是系统级耦合设计变量；zi是系统级传递到第i个子系统的系统级设计变量目标值，zi∈ ｛zshare，zy｝；xi是该子系统的局部设计变量；yi，j是对应于系统耦合设计变量zyi，j的子系统i的第j个子系统耦合状态变量；D（f，）是系统级目标函数对耦合设计变量的导数，上标0代表初始耦合设计变量、x＊i是经过子系统优化后获得的状态变量和局部设计变量值是通过近似技术建立的子系统等式和不等式约束以及状态变量的函数模型；Ji为系统级耦合设计变量目标值与优化后的耦合状态变量值之间的一致性约束，为了加快收敛速度，以绝对值小于ε的不等式约束代替等式约束。其中子系统近似模型的构建在子系统级优化之前，这与BLISS2000对子系统优化的结果建立近似模型不同，不需要进行复杂的系统分析，不必针对优化结果扩展和收缩响应面边界；另外，在对子系统分析建立的近似模型中也包括约束条件，去除了约束的数值噪声，避免了系统级优化的结果在子系统级不可行的问题，同时减少了系统级循环的次数。流程中子系统分析的目的只是为了建立近似模型，故分析只针对设计空间中采集的少量样本点进行，与BLISCO方法相比，避免了每一次系统优化都要进行繁多的子系统分析，从而大大减少了计算量，提高了优化效率，同时对子系统建立近似模型消除了设计空间的数值噪声，可以更高效地找到系统全局最优方案。

2 算例分析

2.1 齿轮减速箱优化问题

齿轮减速箱优化问题（speed reducer problem，SRP）是 NASA（national aeronautics and space administration）评估 MDO方法性能的十大标准算例之一［10］。该问题包含齿轮设计和轴设计，目标是在满足齿轮的弯曲应力和接触应力以及轴的位移和应力等约束条件下使得减速箱的质量最小。它的数学模型［11］如下：

文献［12］给出了该问题的最优解x＊＝ （3.5，0.7cm，17，7.3cm，7.71cm，3.35cm，5.29cm）T，最优目标值f（x＊）＝2994kg。

根据基于近似模型的BLISCO算法，将该问题分为系统级和两个子系统级，分解如下。

系统级：

子系统2：

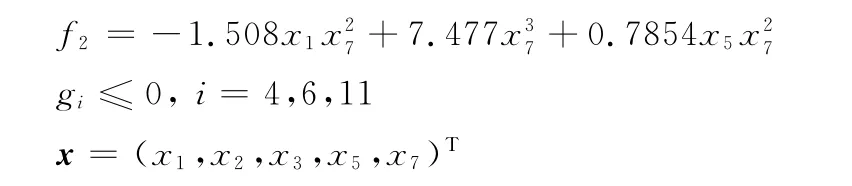
由于子系统的状态变量之间不存在耦合关系，故引入虚拟耦合设计变量。其中系统级设计变量Z＝｛x1，x2，x3，zy1，zy2｝，子系统1局部设计变量X1＝｛x4，x6｝，子系统2局部设计变量X2＝｛x5，x7｝。考虑到该算例函数并不复杂，且响应面模型具有较好的全局近似能力，计算量也不大，故选用二次多项式响应面作为近似模型，具体的算法结构如图3所示。选取五个不同的初始点，各点取值如表1所示。

图3 齿轮减速箱的优化算法结构图

表1 五个不同的初始点的取值

在子系统设计空间中，采用随机选取的方法，选取72个样本点，建立二次多项式响应面模型分别如图4和图5所示。

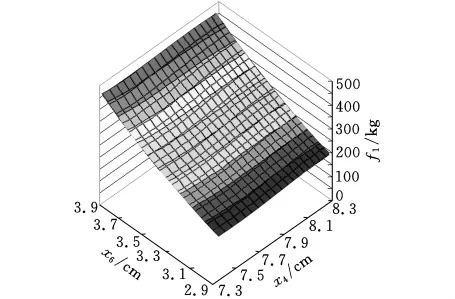
图4 子系统1的二次多项式响应面近似

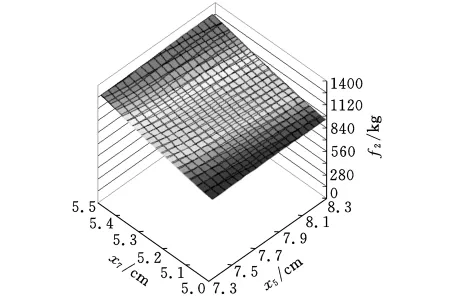
图5 子系统2的二次多项式响应面近似

用多学科设计优化软件iSIGHT建立优化模型，系统级和子系统级均使用序列二次规划优化算法，一致性约束的ε取为0.005。对于5个不同的初始点，用原BLISCO算法求得的优化结果如表2所示。选取同样的初始点和优化算法，响应面近似模型与BLISCO算法结合后求得的优化结果如表3所示。

表2 原BLISCO算法优化结果

表3 近似技术与BLISCO结合后的优化结果

比较分析表2和表3可以看出，无论使用原BLISCO算法还是使用基于近似模型的BLISCO方法，对于不同的初始值，该算例均收敛到稳定的优化解，充分证明了该优化方法的有效性。另外，使用近似模型的BLICO方法虽然系统迭代次数有稍许增加，但相比原BLISCO算法需要1000多次的子系统分析，而建立近似模型只进行了72次的子系统分析而言，优化速度得到了很大提高；由于对子系统的约束和状态变量均建立了近似模型，消除了设计空间的数值噪声，基于近似模型的BLISCO方法获得了比原算法更好的全局最优解，这又体现了该方法的高效性和准确性。且相比其他优化算法如 BLISS2000算法［13］（均值2994.355 955kg）、基于Kriging近似的ECO算法［14］（均值2997.117kg），基于近似模型的BLISCO方法的效果也更好。

以样本点E为例，基于近似模型的BLISCO方法获得系统级和子系统级目标的优化历程如图6所示。

为了考虑近似模型精度对优化结果的影响，对前面构造的近似模型增加了18个样本点，重新构造响应面模型，优化后得到的结果如表4所示。

图6 系统级和子系统级目标的收敛历程

表4 增加样本点后的优化结果

从表4可以看出：增加近似模型精度后，该优化策略获得全局最优解的能力更强，获得的优化解2994.065 23kg与文献［12］给出的最优解2994kg十分接近，这说明近似模型建立的精确度越高，该优化策略获得的结果越准确。

2.2 经典耦合函数优化问题

经典耦合函数是Sellar测试CSSO／RS优化过程的MDO算例［15］，它是一个典型的非线性强耦合优化问题，其数学模型的描述如下：

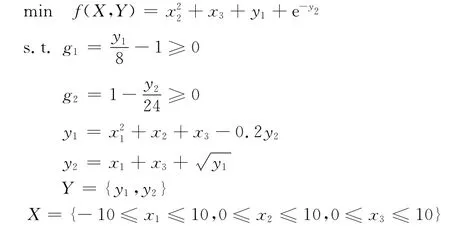
根据基于近似模型的BLISCO算法，首先确定系统级设计变量和子系统级局部设计变量。y1和y2中均含有x1、x3，且y1和y2之间存在耦合关系，故确定系统级设计变量Z＝｛x1，x3，zy1，zy2｝，子系统级局部设计变量为x2。因为y2中不含局部设计变量，不需要对其进行优化，可将其并入系统级优化，子系统1的设计变量X1＝｛x2｝。

最终算法分解如下。

系统级：

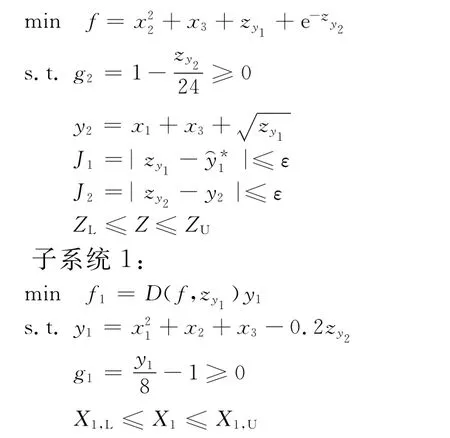
运用多学科设计优化软件iSIGHT对其建立优化模型，y1函数比较简单，故它的函数近似也采用响应面模型。选取4个初始点如表5所示。

表5 四个不同的初始点

用拉丁超立方试验设计方法选30个样本点，对子系统1建立二次响应面模型如图7所示。

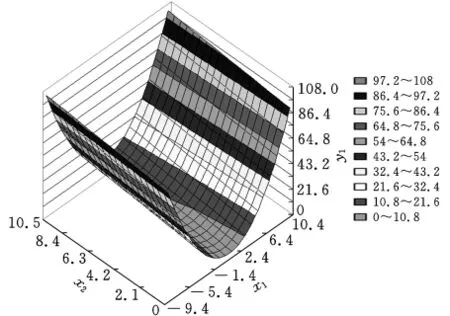
图7 子系统1的近似模型

选取15个样本点对子系统输出响应和约束进行近似误差分析，结果如图8所示。

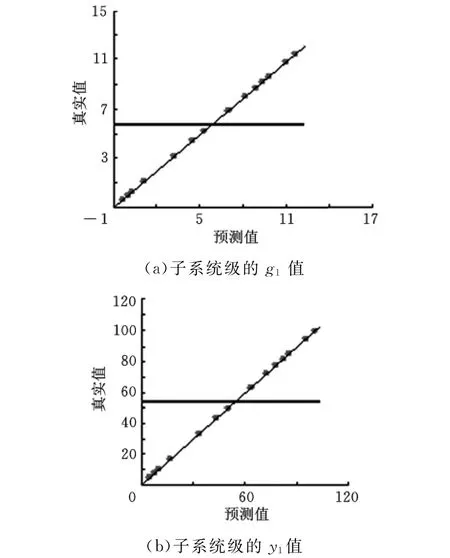
图8 子系统输出和约束真实值和近似值的误差分析

该响应面模型的预测值与实际值趋于一致，输出响应和约束的总误差数量级为10－17，故对子系统1建立的响应面近似模型完全满足精度要求。

系统级优化采用广义简约梯度法，子系统级优化采用NLPQL优化算法，一致性约束的ε取为0.005。对各初始点进行设计优化，用原BLISCO算法求得的结果如表6所示，将近似模型与BLISCO算法结合后获得的优化结果如表7所示。

表6 原BLISCO算法优化结果

表7 近似技术与BLISCO结合后的优化结果

由表7可知，建立近似模型后的系统迭代次数和优化结果同采用精确分析模型的BLISCO算法相同，但避免了反复的子系统分析过程，计算量大大降低，优化效率明显提高。

为了提高非线性约束问题的收敛速度，一致性约束中用含ε的不等式约束代替了严格的等式约束。本文选取了不同数值的ε来研究ε的取值大小对优化结果的影响，当ε取0.05、0.0005、0.000 005时，使用基于近似模型的BLISCO方法求得的优化结果分别如表8～表10所示。

表8 当ε＝0.05时，近似技术与BLISCO结合后的优化结果

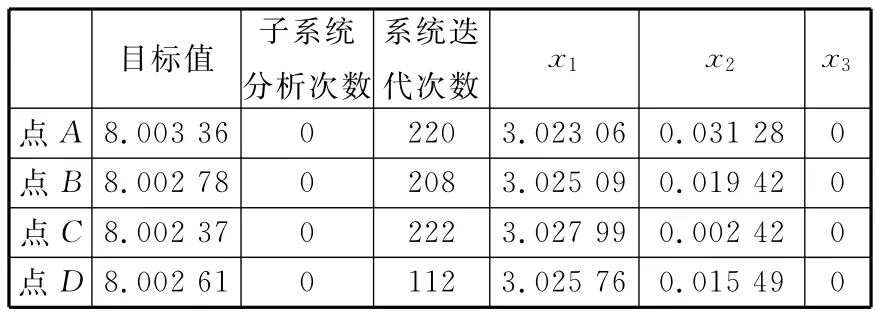
表9 当ε＝0.0005时，近似技术与BLISCO结合后的优化结果

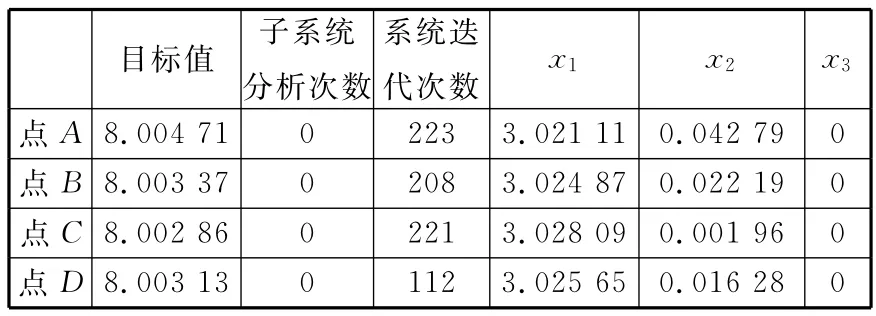
表10 当ε＝0.000 005时，近似技术与BLISCO结合后的优化结果

可以看出，对于不同的ε取值，系统都得到了收敛的优化结果，验证了一致性约束中用不等式约束代替严格等式约束的可行性。且当一致性约束的允许容差减小时，优化结构随初始值变化的波动降低，结果稳定性较好。另外从表中结果来看，进行优化得到最优解的计算量与容差值大小的选取没有太大关系，与初始值的选取相关。

3 结语

本文提出了一种基于近似模型的BLISCO方法，该方法不但保留了BLISCO方法的优点，而且通过用近似模型代替昂贵的子系统高精度仿真模型，达到了提高大规模复杂MDO问题优化效率的目的。通过齿轮减速器算例和经典耦合算例，验证了当子系统之间存在／不存在耦合，以及选取不同初始点条件下，基于近似模型的BLIS－CO方法的可行性和高效性，并获得了比原BLISCO方法以及相关文献所提出方法更好的优化结果。同时，本文对系统级一致性约束的不同允许容差进行了研究，验证了一致性约束中用不等式约束代替严格等式约束的可行性，且允许容差越小，收敛得到的最优解随不同初始点的波动越小，即优化结果更稳定。

目前，本文所采用的算例较为简单，从模型构建效率出发，采用了响应面模型作为近似模型。在以后的研究中，将根据问题特征采用精确度或效率更高的近似模型，并拟将所提出的基于近似模型的BLISCO方法应用到更复杂的工程系统设计中。

［1]Sobiesczanski－Sobieski J.A Linear Decomposition Method for Optimization Problem－Blueprint for Development［R］.Hampton：NASA Technical Memorandum，1982.

［2]Xu L，Yan L，Chen X Q，et al.Enhanced Bi－level Integrated System Synthesis 2000 （EBLISS 2000）［C］／／50th AIAA／ASME／ASCE／AHS／ASC Structures Structural Dynamics and Materials Conference.New York：American Institute of Aeronautics and Astronautics Inc.，2009：1－15.

［3]赵敏，崔维成.BLISCO方法在载人潜水器设计中的应用［J］.船舶力学，2009（2）：259－268.

［4]赵敏.两级集成系统协同优化方法及其在深海空间站总体概念设计中的应用［D］.上海：上海交通大学，2009.

［5]Barthelemy J F，Sobieszczanski－Sobieski J.Optimum Sensitivity Derivatives of Objective Function in Nonlinear Programming［J］.AIAA Journal，1983，21（6）：913－915.

［6]王振国，陈小前，罗文彩，等.飞行器多学科设计优化理论与应用研究［M］.北京：国防工业出版社，2006.

［7]Sakata S，Ashida F，Zako M.Structural Optimization Using Kriging Approximation［J］.Computer Methods in Applied Mechanics and Engineering，2003，192（7／8）：923－939.

［8]Gusciora P H，Foss A S.A Reduced－order Model of a Fixed－bed Reactor Based on a Novel Application of the Taylor Dispersion Approximation［C］／／American Control Conference.Atlanta，1988：1058－1063.

［9]钟毅芳，陈柏鸿，王周宏.多学科综合优化设计原理与方法［M］.武汉：华中科技大学出版社，2006.

［10]Padula S L，Alexandrov N M，Green L L.MDOTest Suite at NASA Langley Research Center，AIAA－1996－4028［R］.New York：American Institute of Aeronautics and Astronautics，1996.

［11]Kodiyalam S.Evaluation of Methods for Multidisciplinary Design Optimization（MDO），CR－1998－208716［R］.Hampton：NASA，1998.

［12]Azarm S，Li W C.Multi－level Design Optimization Using Global Monotonicity Analysis［J］.Journal of Mechanisms，Transmissions，and Automation in Design，1989，111（2）：259－263.

［13]蔡伟，陈小前，姚雯.基于加速收敛BLISS的不确定性多学科设计优化［C］／／高金伍，王国俊.第六届中国不确定系统年会论文集.香港：Global－Link Publisher，2008：25－30.

［14]Xiao M，Gao L，Qiu H B，et al.An Approach Based on Enhanced Collaborative Optimization and Kriging Approximation in Multidisciplinary Design Optimization［J］.Advanced Materials Research，2010，118／120：399－403.

［15]Sellar R S，Batill S M，Renaud J E.Response Surface Based，Concurrent Subspace Optimization for Multidisciplinary System Design，AIAA－1996－0714［R］.New York：American Institute of Aeronautics and Astronautics，1996.