确定非线性隶属度函数的单次聚类方法

王 杰，刘 琪，党勤华

(1.郑州大学电气工程学院，河南郑州450001;2.周口师范学院物理与电子工程系，河南周口466001)

0 引言

具有不确定性的现象与事物，普遍存在于自然界和人类社会中.如何表示和处理不确定性现象与事物，一直是自然科学研究的热点和重点，也是一个瓶颈性问题［1］.Zadeh 博士［2］1965 年发表了模糊集合的开创性成果，提出了利用隶属度来表示事物的亦此亦彼性，隶属度函数的形式主要包括分段线性函数和非线性函数［3］两种.

隶属度函数的确定方法［4］一直没有得到根本解决.实际应用中，隶属度的确定一般采用主观取值，是不可靠的，若采用统计的方法，往往成本很高，有时根本不可能做到.笔者提出了基于密度指标的单次聚类方法，通过曲线拟合，确定了非线性隶属度函数，方法简单，易于推广.

1 非线性隶属度函数

非线性隶属度函数主要有高斯型、sigmoid型、S型、抛物线型等.其中高斯型隶属度函数和sigmoid型隶属度函数具有很好的光滑性，图形没有零点而且具有比较清晰的物理意义，是描述不确定性最为常用的隶属度函数.

高斯型隶属度函数［3］表达式如式(1)，其主要参数是函数中心a和函数曲线的宽度σ，如图1所示.

图1 高斯型隶属度函数Fig.1 Gaussian membership function

sigmoid型隶属度函数［3］表达式如式(2)，适用于“很”、“很不”修饰的语言值的隶属度函数，由b，c两个参数确定，当b为正，sigmoid型隶属度函数曲线向右开口;当b为负，sigmoid型隶属度函数曲线向左开口，如图2所示.

图2 sigmoid型隶属度函数Fig.2 Sigmoid membership function

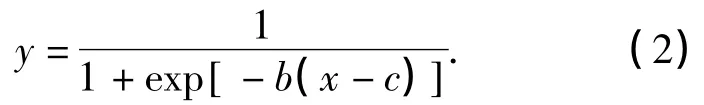
2 单次聚类方法

模糊聚类分析是许多分类和系统建模的基础.聚类的目的是从大量的数据中抽取固有的特征，以获得系统行为的简洁表示.Bezdek提出用隶属度确定数据点属于某个聚类程度的模糊C均值聚类(FCM)方法［5］是目前比较成熟的模糊聚类方法［6］，但算法结果严重依赖随机生成的初始聚类中心.笔者提出一种基于密度指标的单次算法，它的计算量与输入数据数目成线性关系.

对于 X={x1，x2，...，xn} ⊂ RS的样本点集合，单次聚类方法如下：

Step1：设定邻域半径ra、模糊指数b和聚类中心个数m;

Step2：计算每一个点xi的密度指标：

其中，

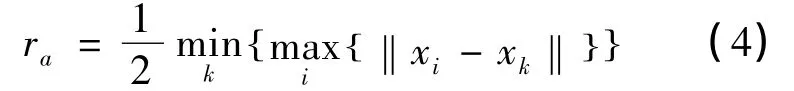
是该点的领域半径，选取最高的密度指标点xc1作为首个聚类中心;

Step3：对每个数据点的密度指标进行修正：

其中，rb是密度指标函数显著减小的邻域半径，一般为rb=1.2ra，取最高的密度指标点xck+1作为新的聚类中心;

Step4：再修订每个数据点的密度指标，直到得到m个聚类中心，将聚类中心定义为wk，k=1，2，...，m;

Step5：计算xi对wk的隶属度uik：

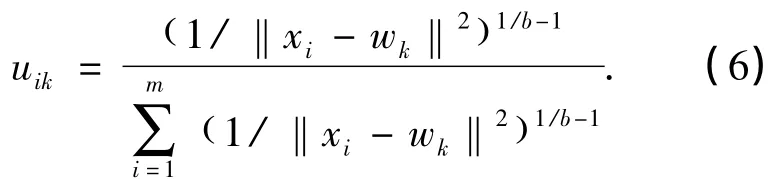
在上述方法中，领域半径ra是某点的密度贡献显著减小的度量，一般采用式(4)确定，实际分析中，只要能得到m个聚类中心，其值大小对聚类结果没有影响，其值越大聚类中心出现越早，但如果过大，得到的聚类中心数目将会小于m.模糊指数b的确定比较复杂，实际分析表明，聚类结果对模糊指数b的变化并不敏感，最佳选取区间为［1.5，2.5］，一般情况下可取 b=2.

3 实例仿真

单次聚类方法可以得到聚类中心和每个数据点对聚类中心的隶属度，这些参数可以确定隶属度函数，仿真实例选用鄂北石油钻井［7］现场总体积数据EB_Da51，确定总体积变化量的隶属度函数，总体积变化量是石油钻井井涌、井漏等事故的主要判别参数之一.EB_Da51中的200个数据分布如图3.

图3 石油钻井中EB_Da51数据Fig.3 Data EB_Da51 of the petroleum drilling

单次聚类方法预设定的聚类中心个数m、聚类得到聚类中心和数据点对聚类中心的隶属度等参数确定隶属度函数的具体方法如下：

Step1：数据统一论域，并根据实际情况确定语言值数目，笔者寻求石油钻井中总体积变化量的隶属度函数，将EB_Da51数据映射到统一的论域空间，取无、小、中、大4个语言值，即m=4.

Step2：单次聚类，求解聚类中心wk和数据对聚类中心的隶属度uik，如图4所示.可以看出，中间语言值基本服从正态分布，可用高斯型隶属度函数表征，两极语言值出现了边缘失真，用sigmoid型隶属度函数曲线表征可以避免这种失真.

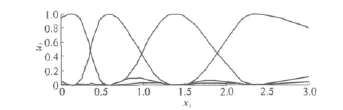
图4 数据变化量的隶属度Fig.4 Membership degree of data variable quantity

Step3：将中间语言值(本例中为“小”和“中”)的论域用高斯型隶属度函数曲线拟合，得到其参数.笔者采用Matlab7中曲线拟合工具箱(Curve Fitting)的Trust-Region方法进行拟合得到参数，如表1所示.

Step4：将两极语言值(本例中为“无”和“大”)的论域用sigmoid型隶属度函数曲线拟合，得到其参数.笔者采用Matlab7中曲线拟合工具箱(Curve Fitting)的Trust-Region方法进行拟合得到参数如表1所示.

表1 隶属度函数的参数Tab.1 Parameters of membership function

Step5：根据曲线拟合得到的参数，可以确定隶属度函数如图5所示.

图5 EB_Da51的隶属度函数Fig.5 Membership function of data EB_Da51

4 结论

经实例研究表明，笔者提出的单次聚类方法不需迭代，避免了模糊均值聚类方法容易陷入局部极小点的可能性，快速得到了聚类中心和数据的隶属度，它的计算量仅与输入数据数目成线性关系.采用单次聚类方法，通过曲线拟合确定了高斯型和sigmoid型隶属度函数，解决了非线性隶属度函数难以确定的难题.

［1］李德毅.知识表示中的不确定性［J］.中国工程科学，2002(10)：73-79.

［2］ZADEH L A.Fuzzy sets［J］.Information and Control，1965(8)：338-353.

［3］黄士涛，胡全义，马进元，等.自适应神经模糊推理系统在起重机稳钩控制中的应用［J］.郑州大学学报：工学版，2007，28(1)：21-25.

［4］陆建江，张亚非，宋自林.模糊关联规则的研究与应用［M］.北京：科学出版社，2008：43-51.

［5］刘琪，张鸿辉，黄贞贞.基于模糊C均值聚类方法的石油钻井工作状态分析［J］.周口师范学院学报，2009(5)：47-49.

［6］黎灿兵，曲芳，王晓宁，等.基于模糊聚类的电力系统负荷特性分析［J］.郑州大学学报：工学版，2010，29(1)：107-110.

［7］王杰，陈东海，朱晓东，等.基于分层模糊系统的石油钻井事故预警系统：中国，200710055178.6［P］.2007-06-01.