挠性航天器姿态机动时间最优控制研究

何海锋,曾海波

(1.北京控制工程研究所,北京100190；2.空间智能控制技术重点实验室,北京100190)

挠性航天器姿态机动时间最优控制研究

何海锋1,2,曾海波1,2

(1.北京控制工程研究所,北京100190；2.空间智能控制技术重点实验室,北京100190)

针对挠性航天器单轴姿态快速机动的控制问题，将系统的模型处理成非约束模型，采用极小值原理求解了问题的时间最优控制律，并结合边值条件推导了时间最优控制的切换时间应满足的充要条件.利用切换时间所满足的非线性方程组分析和证明了时间最优控制的对称性及满足的条件：在不考虑阻尼系数时，问题的时间最优控制是机动时间上的对称函数.利用这个规律，对刚体+1阶挠性模态的时间最优姿态机动问题进行了解析求解.针对挠性模态阶次较高时难以求解非线性方程组的问题，将模型离散化，把问题处理成一系列受约束的最小二乘优化问题来求解，数学仿真表明了该方法的有效性.

挠性航天器；姿态快速机动；时间最优控制

航天器在轨运行时,由于任务需要,需要具有姿态快速机动和稳定能力.最初,航天器被简化为刚体模型,由此得到了经典的时间最优“Bang-Bang”控制规律［1］.文献［2-4］对刚体的三轴姿态机动时间最优控制进行了研究,文中对时间最优的旋转轴进行了分析和讨论.文献［2］和文献［3］均对刚体模型转动惯量做了限制,以此消除动力学方程中的陀螺力矩非线性项,使得系统保持线性特性.文献［4］考虑了陀螺力矩非线性项,取得了较好的结果.

刚体航天器的时间最优姿态机动问题已经取得了较为成熟的成果,对挠性航天器姿态机动最优控制的研究,最早的成果见于文献［5］.文中考虑单轴挠性航天器模型的动力学特性,将其看作约束模型,为了不激起挠性模态的振动,根据所给的期望姿态角,结合动力学方程设计姿态角的变化曲线,按此完成姿态机动后,挠性模态的振动最小.之后,以一个中心刚体+挠性附件为模型的单轴旋转机动问题得到了广泛的研究［6-15］.文献［6-7］运用线性二次型调节器对以控制量和系统能量作为性能指标的问题进行了求解.文献［8］研究了以控制量和时间为性能指标的喷气推力最优控制问题.文献［9-10］则把机动时间和机动完成后的剩余能量作为性能指标,得出了近似最小时间控制的结果.

挠性航天器姿态机动的纯时间最优控制以文献［11］开始,文中用相平面方法来研究带有1阶挠性模态模型的时间最优问题.文献［12-13］针对无阻尼的挠性航天器,将其转化为非约束模型,利用极小值原理列出了时间最优控制满足的充分必要条件,且通过仿真曲线说明了控制输入的对称性.文献［14］研究了挠性航天器模型中挠性模态频率和阻尼系数这两个参数对机动时间的影响.最近的研究见于文献［15］,文中利用时间最优控制的规律来规划方波控制序列,对不考虑阻尼系数的挠性航天器姿态快速机动取得了较好的控制效果.

挠性航天器的姿态快速机动问题,仍然需要采用最优控制的方法实现姿态机动时间最优.因为挠性航天器的三轴姿态机动不仅有刚体姿态的非线性项,还有挠性模态的非线性项,为了便于研究,本文依然以挠性航天器的单轴姿态机动为研究对象.对于文献［12-13］中提出的控制输入的对称性,本文将给出其成立的条件和证明,利用这一规律可以简化两点边值问题的解析求解.对于挠性模态阶次较高的情形,本文引入了基于离散模型的约束线性最小二乘优化方法,完成了数学仿真,并得出了一般情况下切换次数与挠性模态阶次的对应关系、机动时间随挠性模态阶次增加的变化规律.

1 系统与问题描述

以俯仰轴姿态角θ为例,令挠性附件转动的角速度ωa=0,则单轴挠性航天器的动力学方程［16］为(考虑挠性附件自身阻尼)

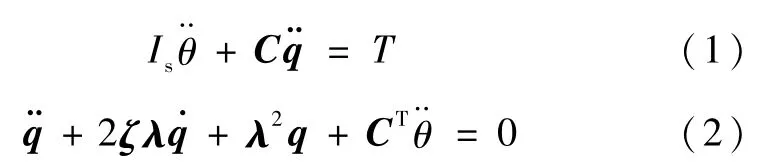
式中,Is为俯仰轴的转动惯量,θ为姿态角,q为模态坐标(考虑n阶)为模态藕合系数行为模态阻尼对角阵为模态频率对角阵T为作用在中心刚体上的姿态控制力矩.

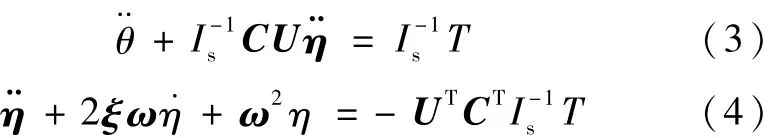
定义如下的状态和控制变量:

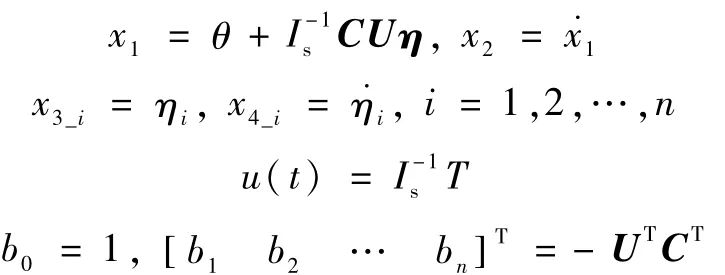
定义

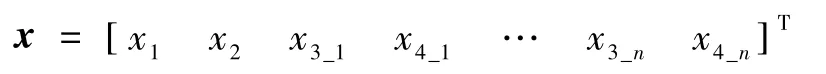
则,式(3)～(4)可写为如下形式:

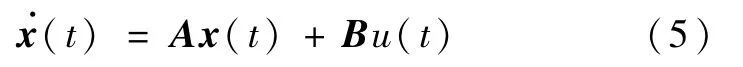
式中,A=block diag｛A0,A1,A2,…,An｝,block diag｛·｝表示以其中元素矩阵

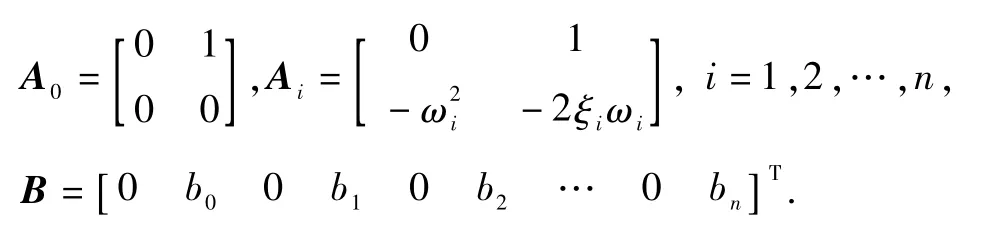
“静止到静止”的时间最优姿态机动问题,就是选择满足

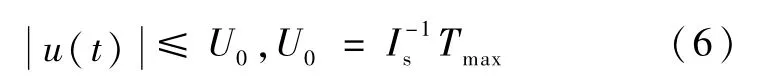
的标量控制函数u(t),使得式(5)描述的系统从初始状态

转移到最终状态

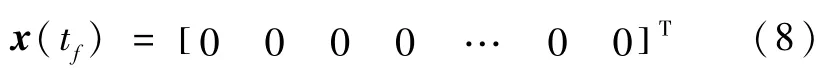
的机动时间tf最小,即最小化如下的性能指标函数

2 控制方法

上述系统(5)是线性定常,而且完全能控.

引理1.若线性定常系统(5)是完全能控的,则式(5)～(9)所描述的时间最优控制问题是正常的(即u( t)仅在有限个数的切换点处为0).

引理2.对式(5)～(9)所描述的时间最优控制问题,若矩阵A的特征值均具有非正的实部,则从任意初态转移到坐标原点的时间最优控制存在.

引理3.对式(5)～(9)所描述的时间最优控制问题,若问题是正常的,则时间最优控制是含有若干次切换的“Bang-Bang”控制.

引理4.若式(5)～(9)所描述的时间最优控制问题是正常的,且时间最优控制存在,则最优控制必唯一.

以上引理的相关证明参见文献［1］.

由以上引理可知,式(5)～(9)所描述的时间最优控制问题是含有若干次切换的“Bang-Bang”控制,且最优控制是唯一的.

由极大值原理,时间最优控制为

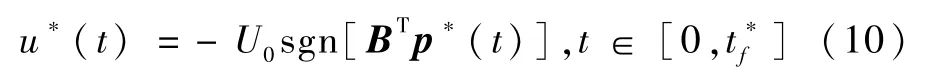
其中,*表示最优控制,符号函数定义为

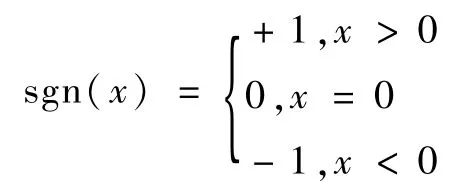
协态方程

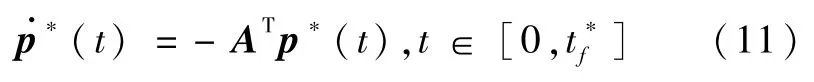
式中,协态向量

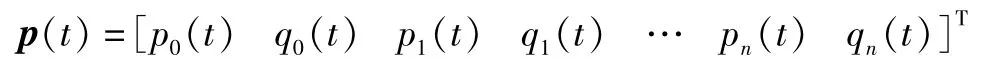
哈密顿函数

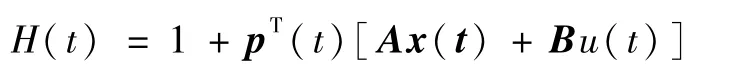
满足

由式(10)所描述的最优控制可知

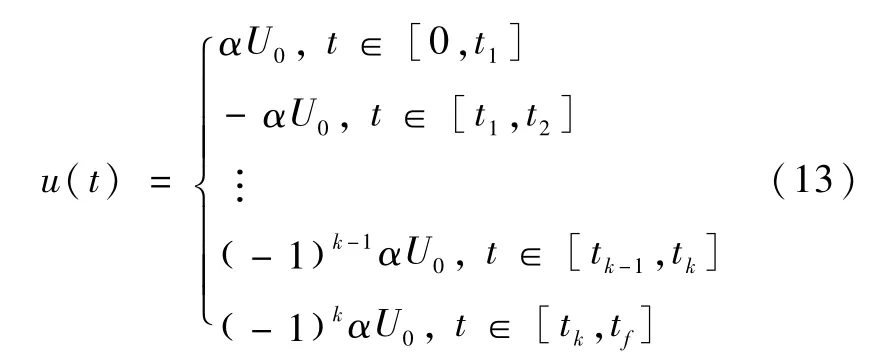
式中,t1,t2,t3,t4,…,tk表示切换时间,共有k次切换,tf表示机动时间,α表示初始时刻u()0的符号.

由式(5)可得

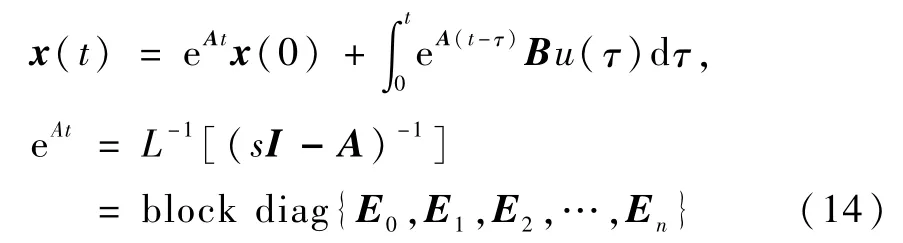
其中,L-1(·)表示求拉普拉斯反变换.

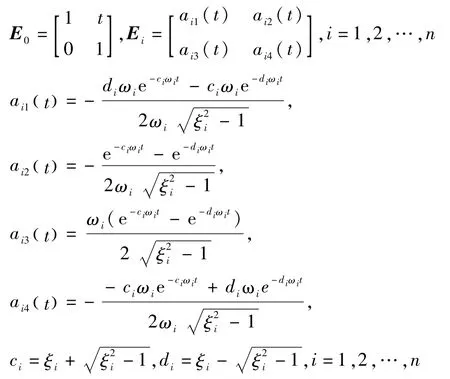
将边值条件(7)～(8)和控制输入(13)代入(14)整理得

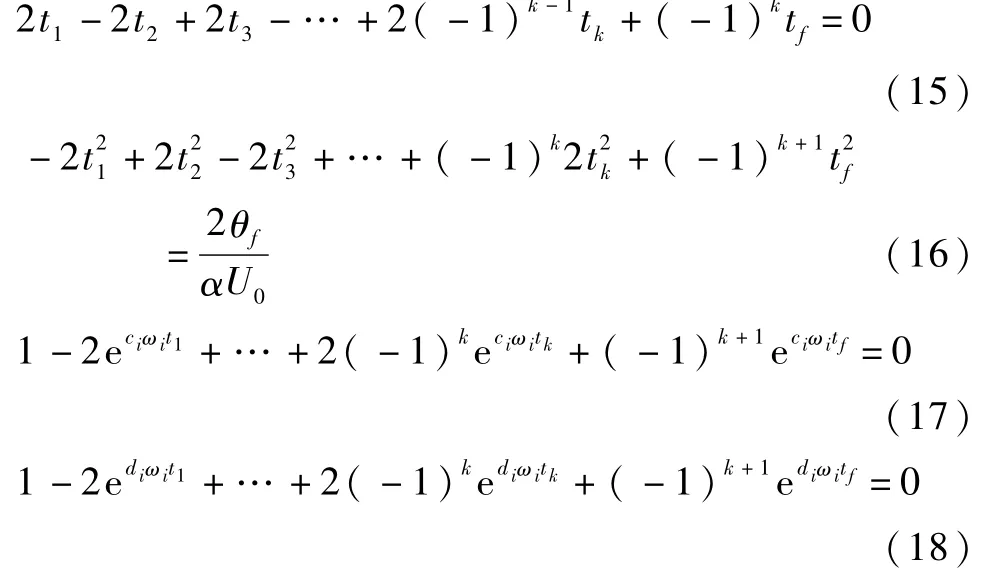
式(17)和(18)中i=1,2,…,n.

式(11)表明

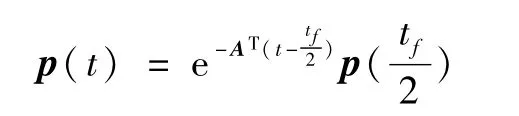
时间最优控制中符号函数的变量满足在切换时刻

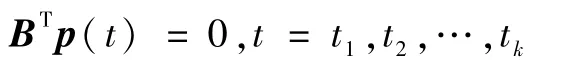
即

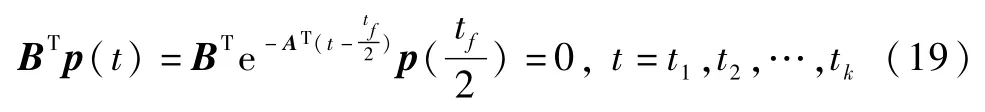
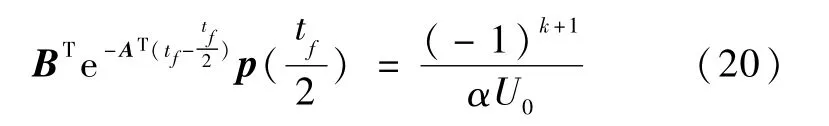
整理式(19)和(20),可得

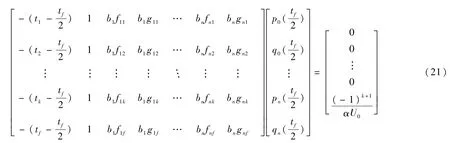
其中,

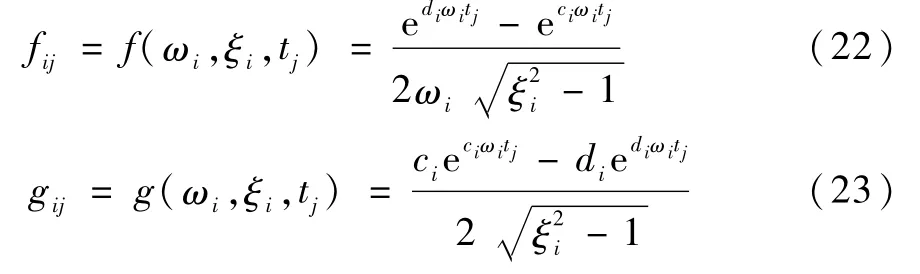
式(22)～(23)中i=1,2,…,n；j=1,2,…,k,f.

式(15)～(18)和(21)组成了2+2n+(k+1)个非线性方程.而未知量有:k+1个时刻t1,t2,…,+2n+(k+1)+1个.

此外,满足式(15)～(18)和(21)组成的非线性方程组的解还必须满足

式(15)～(18)、(21)和(24)构成了时间最优控制的切换时间的充分必要条件.

3 最优控制的对称性分析

3.1 阻尼系数ξi=0，i=1，2，…，n的情形

ξi=0,i=1,2,…,n时,式(17)～(18)化为

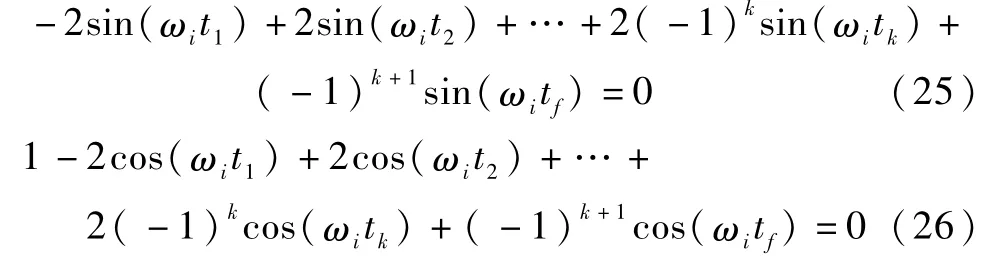
式(25)～(26)中i=1,2,…,n.

由式(10)～(11)可得ξi=0,i=1,2,…,n时,式(22)～(23)化为

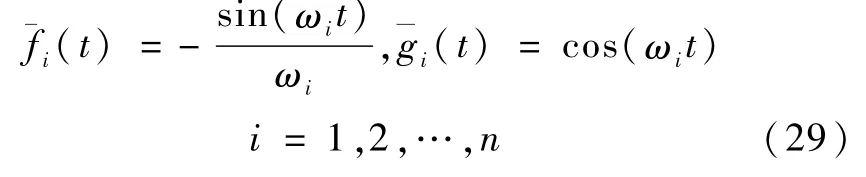
式(27)中

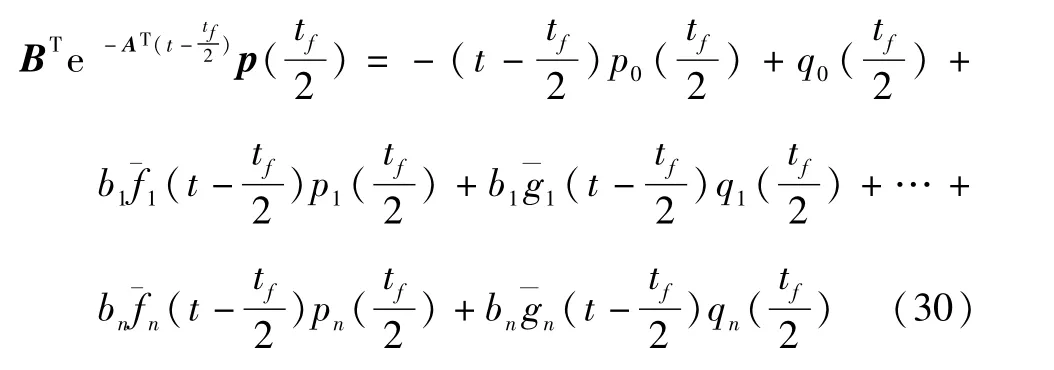
式(28)中

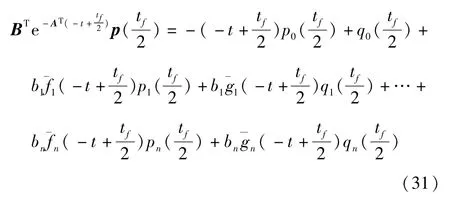
a)当k为奇数时,设k=2m+1,m=0,1,2,…,将式(21)前k行中的1,3,…,2m+1行分别乘以-1再与剩下的 2,4,…,2m行加在一起,并将式(15)～(16)、(25)～(26)代入,可得

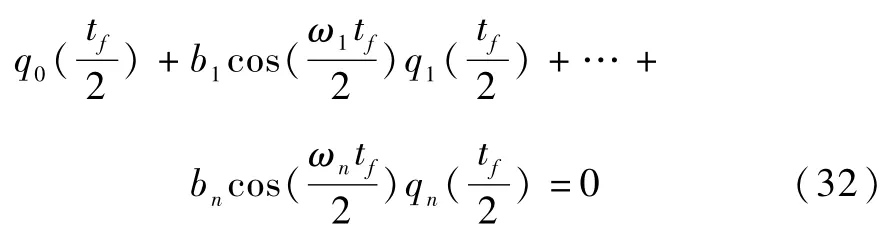
因为b1,b2,…,bn≠0,而tf是与任意给定的θf对应的,要式(32)恒成立,必要求

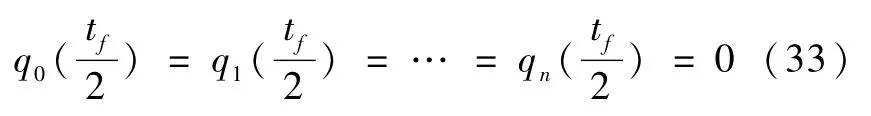
将(30)～(31)、(33)代入(27)～(28)得,t∈［0,

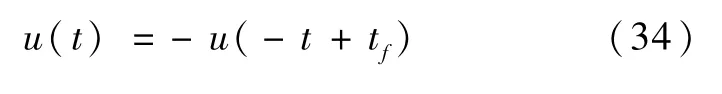
b)当k为偶数时,同以上方法可得

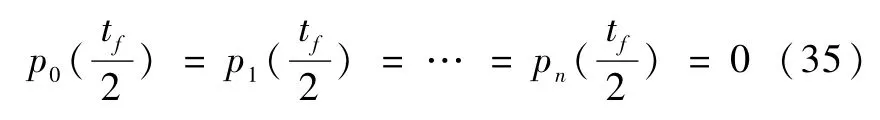
将(30)～(31)、(35)代入(27)～(28)可得,t∈［0,

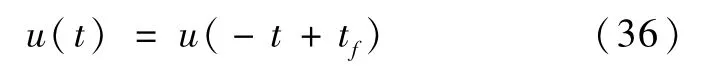
而由系统状态方程(5)可得

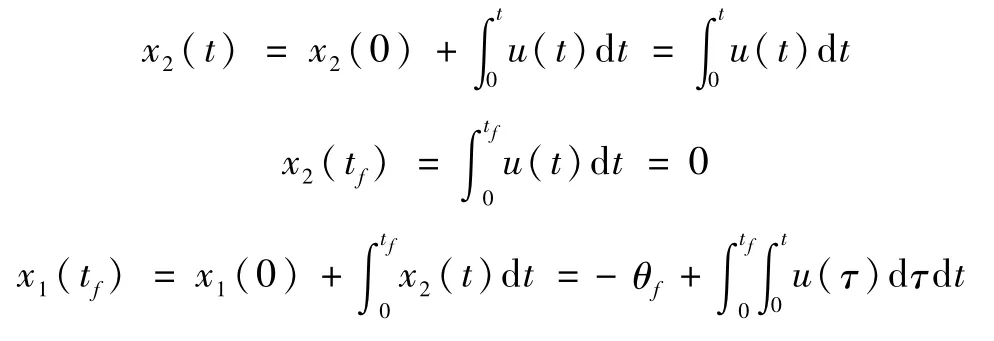
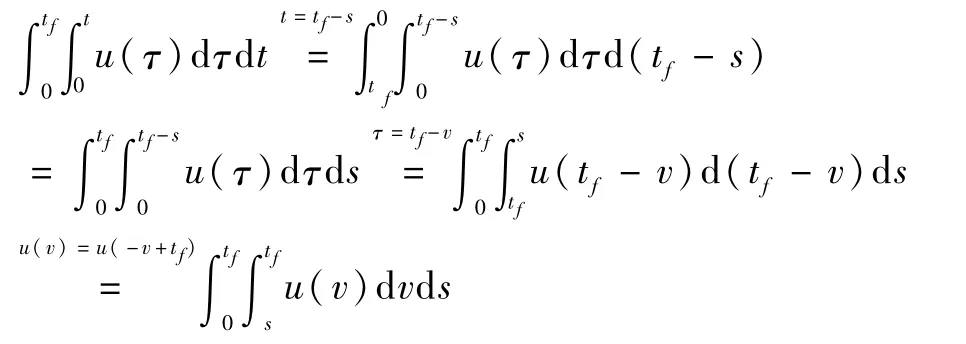
于是,

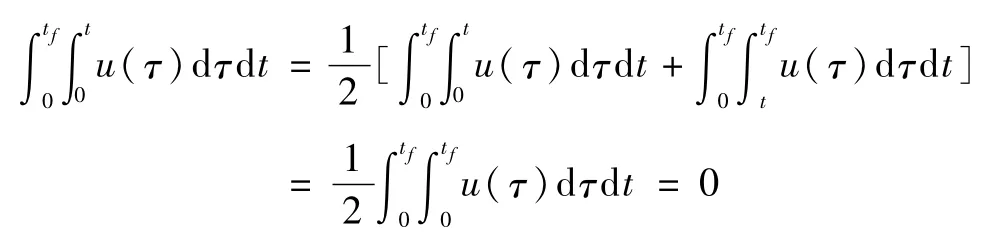
得到x1(tf)=-θf,这是与终端条件x1(tf)=0相矛盾的,故k为偶数不成立.因此,k必为奇数,u(t)具有对称性,且满足

3.2 阻尼系数ξi≠0，i=1，2，…，n的情形

此时u(t)和u(-t+tf)及相关项的表达式仍形如(27)～(28)、(30)～(31)所示,但因式(22)～(23)中fij(t)和gij(t)在时间t上均不具有对称性,所以,此时控制量u(t)也不具有对称性.

4 解析方法求解

利用上面的规律:当ξi=0,i=1,2,…,n时,k必为奇数,u(t)具有对称性.可以将关于切换时间的非线性方程组(15)～(16)、(25)～(26)中的未知量的个数减少一半.

取n=1,ξ1=0时,根据文献［12］的仿真结果,假设u(t)的初始符号α=sgn(θf),且有不多于3次切换.由u(t)的对称性知,第一次和第三次的切换时间t1、t3关于中间第二次切换时间可设t2-t1=t3-t2=ta,则t1、t2、t3表示为

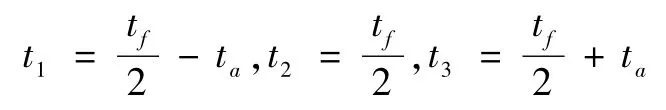
代入方程组(15)～(16)、(25)～(26),整理得

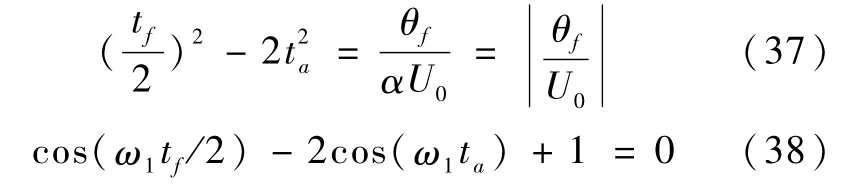
又由式(21)可得

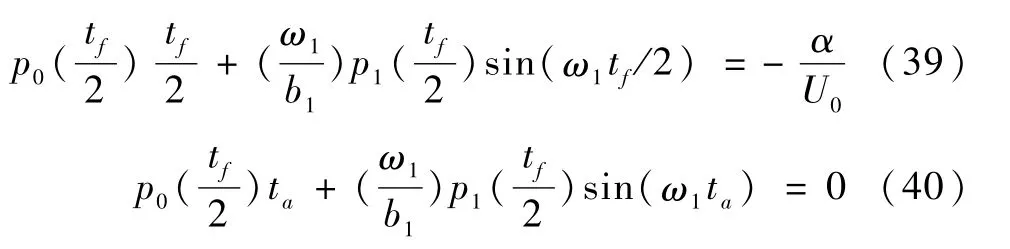
满足式(37)～(40)的解还必须满足

式(37)～(41)构成了时间最优控制的充要条件,因此,满足(37)～(41)的解必是时间最优控制所对应的切换时间.

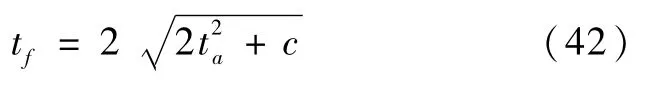
代入式(38)可得,

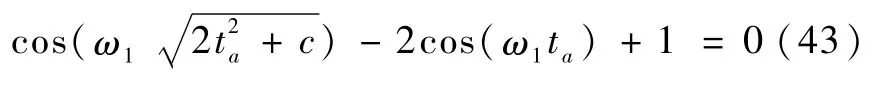
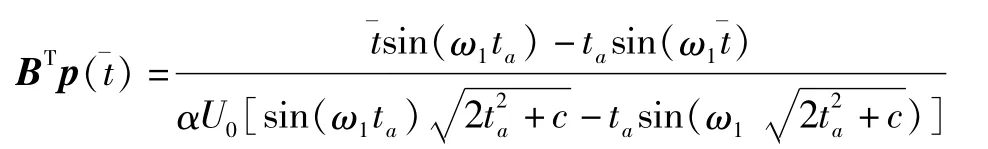
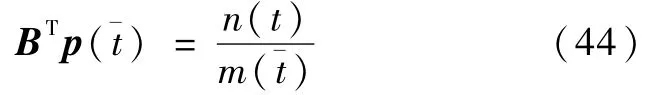
i)当ta=0时,t1=t2=t3,仅有一次切换,而且仅当=0时, BTp(=0,满足时间最优控制充要条件.此时,时间最优控制是类似于刚体模型的情形.

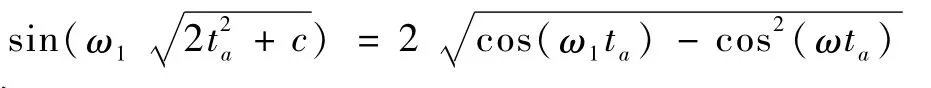
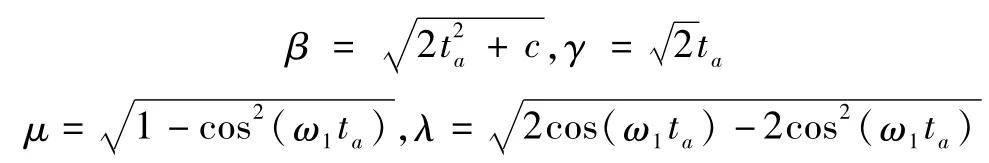
然而,对于模态阶次较高的情形,关于时间最优控制的切换时间和机动时间的非线性方程维数也相应较多,求解它们是一项很复杂的工作,需要寻找更高效的方法.

总结1.对于n=1,ξ1=0的情形,切换次数一般为3次.仅在期望姿态角满足条件

5 数值方法求解

［14］基于离散化的模型,将问题处理成一系列受约束线性最小二乘优化问题,给出了一种新的求解方法.

采用零阶保持器,将连续系统(5)化成如下的离散形式

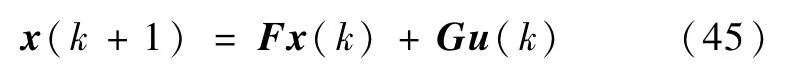
其中

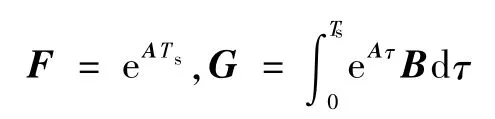
Ts是采样时间,于是,由递推式(45)可得

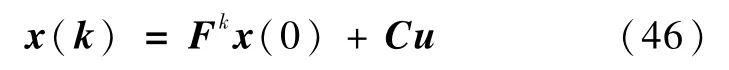
其中,C矩阵表示为

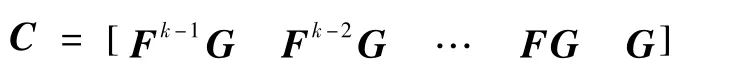
u是由各时刻控制量所组成的向量

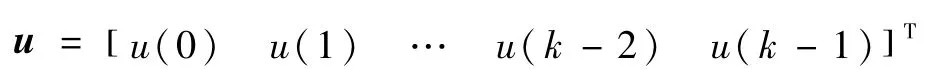
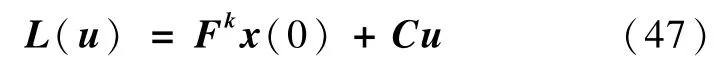
在式(46)中,x(k)为u的函数.故可设初始状态x(0)和终端状态x(tf)由式(7)～(8)给定.

于是,前面的时间最优控制问题可以描述为如下的一系列受约束的最小二乘问题:需要找到一个最小的k,并求取一个对应的控制向量 u(其tf=kTs.

6 数值仿真实例

仿真参数Is=1500kg·m2,力矩T≤150N·m,变换后对应(5)中的ω1=1.5rad/s,ω2=3.1rad/s, ω3=7.5rad/s(以三阶挠性模态为例分析),阻尼系数ξi=0,i=1,2,3,b0=1,b1=1,b2=0.3,b3=0.1,期望机动的姿态角θf=60°=1.047 rad.

为了节省仿真时间,先解析计算刚体的时间最优控制姿态机动时间.

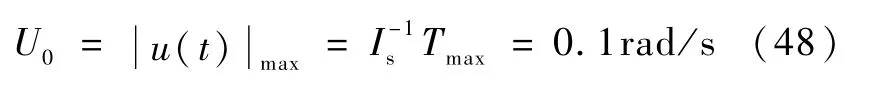
刚体的时间最优控制姿态机动为仅有一次切换的“Bang-Bang”控制.于是

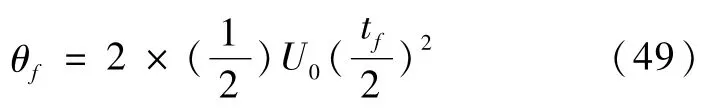
若取采样时间Ts=0.01s,刚体的机动时间是最小的,则k的值可以从小于刚体时间647的附近选,如可取k=600开始计算,这样就减少了600步的最小二乘优化步骤,节省了仿真时间.

图1～4是系统(5)分别以刚体、刚体+1阶、2阶、3阶挠性模态为模型时姿态机动时间最优控制随时间的变化曲线,从图中可以看出,控制量切换次数分别为1、3、5、7次,机动时间分别为tf=6.47s、6.67s、6.70s、6.71s.仿真结果表明,若考虑系统是刚体+n阶挠性模态的无阻尼模型,则问题的时间最优控制一般有2n+1次切换(不计t=0和t=tf时刻).而且,机动时间tf的增加量随模态阶次的增加越来越小.

系统(5)在图 1～4的控制量作用下姿态角θ(t)的响应曲线如图5所示,机动完成后的姿态响应曲线局部如图6所示,曲线表明,控制的挠性模态阶次越多,姿态机动完成后姿态的稳定度越高,在实

求解可得刚体的时间最优控制姿态机动时间为际工程中应该根据稳定度的要求,确定需要控制的挠性模态阶次.

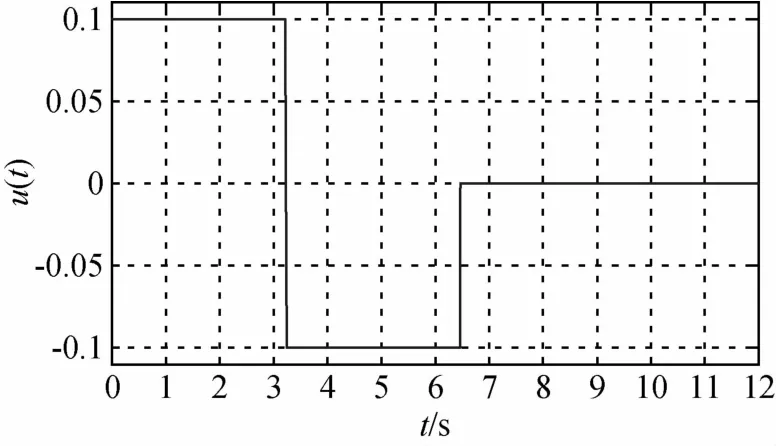
图1 刚体的姿态机动时间最优控制Fig.1 Time-optimal control for attitude maneuver of rigid body

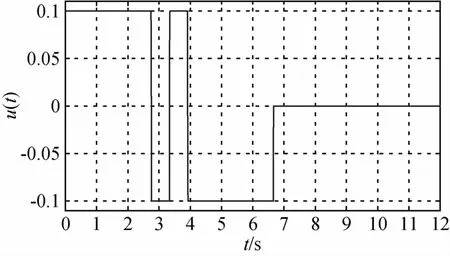
图2 刚体+1阶挠性姿态机动时间最优控制Fig.2 Time-optimal control for attitude maneuver of rigid body with one flexible mode

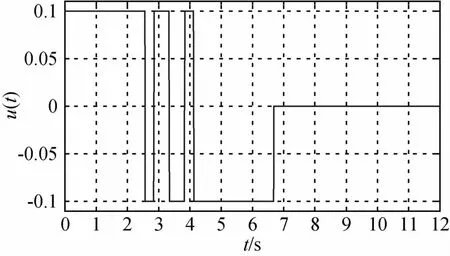
图3 刚体+2阶挠性姿态机动时间最优控制Fig.3 Time-optimal control for attitude maneuver of rigid body with two flexible modes

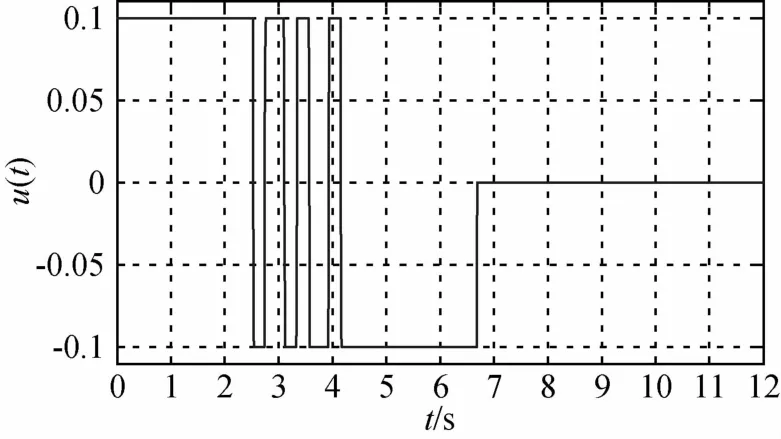
图4 刚体+3阶挠性姿态机动时间最优控制Fig.4 Time-optimal control for attitude maneuver of rigid body with three flexible modes

当阻尼系数不可忽略时,如取ξi=0.2,i=1, 2,3,为了对比方便,不妨取刚体+3阶挠性模态的模型,姿态机动时间最优控制随时间变化曲线如图7所示,对比图4可知,其在机动时间上不具有对称性.

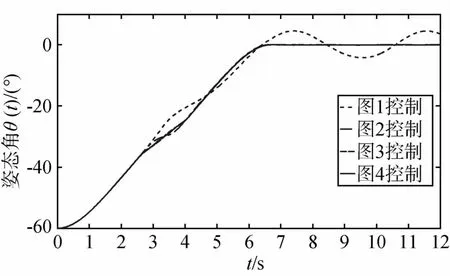
图5 控制量作用下的姿态角θ(t)响应曲线Fig.5 Attitude-time historiy under optimal control

图7 阻尼系数ξi=0.2,i=1,2,3时,刚体+3阶挠性姿态机动时间最优控制Fig.7 Time-optimal control for attitude maneuver of rigid body with three flexible modes,damping factorξi=0.2,i=1,2,3

7 结 论

对挠性航天器单轴姿态快速机动的控制问题,本文利用极小值原理,求解了时间最优控制律.结合边值条件推导了时间最优控制的切换时间应满足的充要条件,并利用其所满足的非线性方程组分析了控制量的对称性及满足的条件.在不考虑阻尼系数时,利用控制量的对称性可以将非线性方程组的未知量个数减半,极大地简化了求解的难度.然而,考虑高阶挠性模态时,求解非线性方程组的计算量仍然很大,更高效的求解方法还有待寻求.为此,文中引入了离散模型的约束最小二乘优化方法完成数值仿真,仿真结果也验证了控制量的对称性.同时,仿真结果显示了一般情况下切换次数与挠性模态阶次的对应关系、机动时间随挠性模态阶次增加的变化规律,这些规律还有待进一步地分析和证明.机动完成后的姿态响应曲线表明:控制的挠性模态阶次越多,机动完成后姿态的稳定度越高.如何给出其精确的定量描述,这也有待解决.

参 考 文 献

［1］ 解学书.最优控制理论与应用［M］.北京:清华大学出版社,1986,167-189 Xie X S.Optimal control theory and application［M］. Beijing:Tsinghua University Press,1986,167-189

［2］ Bilimoria K D,W ie B.Time-optimal three-axis reorientation of a rigid spacecraft［J］.Journal of Guidance, Control,and Dynam ics,1993,16(3):446-452

［3］ Bai X L,Junklins JL.New results for time-optimal reorientation of a rigid spacecraft［J］.Journal of Guidance,Control,and Dynam ics,2009,32(4):1071-1076

［4］ Andrew F,Pooya S,Ross IM.M inimum-time reorientation of a rigid body［J］.Journal of Guidance,Control, and Dynam ics,2010,33(1):160-170

［5］ Farrenkopf R L.Optimal open-loop maneuver profiles for flexible spacecraft［J］.Journal of Guidance,Control,and Dynam ics,1979,2(6):491-498

［6］ Turner JD,Junkins JL.Optimal large-angle single-axis rotationalmaneuvers of flexible spacecraft［J］.Journal of Guidance,Control,and Dynamics,1980,3(6): 578-585

［7］ Turner JD,Chun H M.Optimal distributed control of a flexible spacecraft during a large angle maneuver［J］. Journal of Guidance,Control,and Dynamics,1984,7 (3):257-264

［8］ Velde V,He W J.Design of space structure control system using on-off thruster［J］.Journal of Guidance, Control,and Dynamics,1983,6(1):53-60

［9］ Thompson R C,Junkins J L,Vadali S R.Near-m inimum time open-loop slewing of flexible vehicles［J］. Journal of Guidance,Control,and Dynamics,1987,12 (1):82-88

［10］ Byers R M,Vadali S R,Junkins J L.Near-minimum time,closed-loop slewing of flexible spacecraft［J］. Journal of Guidance,Control,and Dynamics,1990,13 (1):57-65

［11］ Barbieri E.Rest-to-rest slewing of flexible structures in m inimum time［C］.The 27thConference on Decision and Control,Texas,USA,December 1988

［12］ Singh G,Kabamba P T,McClam roch N H.Planar, time-optimal,rest-to-rest slewing maneuvers of flexible spacecraft［J］.Journal of Guidance,Control,and Dynam ics,1989,12(1):71-81

［13］ Asher B J,Burns JA,Cliff E M.Time-optimal slewing of flexible spacecraft［J］.Journal of Guidance,Control,and Dynamics,1992,15(2):360-367

［14］ Pao L Y.M inimum-time control characteristics of flexible structures［J］.Journal of Guidance,Control,and Dynamics,1996,19(1):123-129

［15］ 张洪华,黎康,赵宇.挠性卫星姿态快速机动控制［J］.中国空间科学技术,2005,25(1):53-59 Zhang H H,Li K,Zhao Y.Fast maneuver control of flexible satellites system［J］.Chinese Space Science and Technology,2005,25(1):53-59

［16］ 章仁为.卫星轨道姿态动力学与控制［M］.北京:北京航空航天大学出版社,1998 Zhang R W.Dynamics and control of spacecraft orbit and attitude［M］.Beijing:Beijing University of Aeronautics and Astronautics Press,1998

Tim e-Op tim al Control for Flexib le Spacecraft A ttitude M aneuver

HE Haifeng1,2,ZENG Haibo1,2
(1.Beijing Institute of Control Engineering,Beijing 100190,China；2.Science and Technology on Space Intelligent Control Laboratory,Beijing 100190,China)

The problem of single-axis fast attitude maneuver for a flexible spacecraft is considered in this article.By converting the system into unconstrained model and applying the Minimum Principle,the solution for time-optimal control is obtained,while the necessary and sufficient condition for the controlswitching time are also established under boundary value conditions.By analyzing the nonlinear equations of the switching time,it is found that if the damping coefficient can be negligible,the control input for time-optimal attitudemaneuver will be a symmetrical function of the maneuver time,and the complexity of solving the nonlinear equations could be reduced greatly.Based on this kind of symmetry,an analytic solution for the rigid body with only one flexible mode is obtained.To overcome the difficulty in solving the nonlinear equations with large number of flexible modes,the system is then transformed into a discrete-timemodel and further simplified to a set of constrained least-squares problems.Finally,numerical simulation is conducted to demonstrate the effectiveness of the method.

flexible spacecraft；fast attitude maneuver；time-optimal control

V448

A

1674-1579(2012)01-0010-08

何海锋(1986-),男,硕士研究生,研究方向为航天器姿态控制；曾海波(1972-),男,研究员,研究方向为航天器智能控制.

2011-09-29

DO I:10.3969/j.issn.1674-1579.2012.01.002