基于突变理论的城市配水系统脆弱性评价模型

牛志广，姜 巍，陆仁强，张宏伟

(天津大学环境科学与工程学院，300072天津)

城市配水系统是一个极其复杂的系统，很容易受到蓄意破坏、系统事故、自然灾害等多种威胁.根据以往研究成果可知［1］，城市供水风险的大小由威胁发生的概率、严重程度及系统自身脆弱性3个因素决定.配水系统面临威胁(本文以地震灾害为例)的严重程度和发生概率是人为无法控制的，但是，供水部门可以改变结构参数使配水系统的脆弱性降低，达到对供水风险的控制.另一方面，配水系统脆弱性是其在特定的威胁发生时，由于社会、经济、自然等多个因素的作用，所表现出的固有敏感性和人类应灾能力，因此，配水系统的脆弱性是针对特定威胁的.以往在配水系统脆弱性评价方面的研究，多借助于数值分析模型，以机理性研究为主［2－3］，但是，配水系统脆弱性由管径、管材、接口形式和周边环境等多个控制变量决定，配水系统的复杂性使得这些机理性研究不太适合实际管理的需要.为此，根据地震发生时配水系统供水功能转变的突变特征，结合以往的研究基础，建立了基于突变理论的配水系统脆弱性综合评价数学模型.

1 突变理论基础

在社会或自然现象中，如地震的发生、水的沸腾等，这种由量变、渐变的过程发展到突变、质变的过程随处可见.为有效解决上述非连续的突变过程，法国数学家Rene Thom基于拓扑学、结构稳定性等数学基础提出了突变理论.Rene Thom证明，当系统的控制变量ui的个数不多于4，状态变量xi的个数不超过2时，最多有7种基本突变形式［4］.突变理论在研究某种过程从某一稳定态跃迁到另一稳定态时，首先假设系统的状态可以用一组参数表征，当系统处于某一稳定态时，对应这一稳定态的函数便取唯一的极值，而当参数在一定范围变化，其函数的极值大于1个时，该系统便处于不稳定态.当系统从一种稳定态进入某个不稳定态时，参数的微小变化便可使系统从不稳定态转入一种新的稳定态，系统的状态便在这一瞬间发生突变.突变理论的主要优势就是通过对临界点附近非连续变化现象的分析来实现对突变过程的解释.因此，突变理论在物理、化学及社会科学等多学科都得到广泛应用［5-6］.

2 基于突变理论的配水系统脆弱性综合评价模型

2.1 配水系统脆弱性评价指标体系

根据上述脆弱性的定义可知，配水系统的脆弱性指数(V)由灾损敏感性(Vs)和应灾能力(Vd)两个评价指标共同决定.灾损敏感性由配水系统的自身结构特征决定，是其遭受某一特定威胁后的损失程度，而配水系统应灾能力是供水部门为保障配水系统在特定威胁作用下的供水安全而采取的措施，反映了供水部门应对威胁发生时的主观能动性.

根据大量历史地震资料及刘遂庆等对2008年“5.12”特大地震现场调研资料分析可知［7－8］，配水系统的抗震能力主要由管径、管材、连接方式、管龄及所在区域的土壤环境5个因素决定，因此，本文从这几个方面对配水系统面临地震威胁时的灾损敏感性进行评价.而与配水系统相伴的人类应灾能力从人力、财力、物力等3方面进行评价，考虑到这几个因素均与配水系统所在城市的经济地位有直接关联，通常配水系统所属城市的经济实力越雄厚，用于防震减灾及灾后重建的资金就越有保障，配水系统恢复正常供水功能的时间就越短，建立如下配水系统脆弱性评价指标体系(见表1、2).

表1 配水系统脆弱性评价指标体系1

表2 配水系统脆弱性评价指标体系2

2.2 配水系统控制变量的选择及尖点突变模拟

根据突变理论可知，配水系统不连续构造的个数只由控制变量ui的个数确定，而与状态变量xi无关.本文将配水系统的整体脆弱性指数V作为状态变量，将灾损敏感性指数Vs、应灾能力指数Vd作为配水系统的控制变量.根据历史资料分析可知，配水系统脆弱性主要由Vs决定，而Vd的贡献次之，因此，将Vs作为主控制变量u1，Vd作为次控制变量u2.

根据突变理论，对于配水系统尖点突变现象，描述该配水系统的势函数为

因此，配水系统的供水功能状态可以用3维空间中的相点(V，Vs，Vd)表示，为避免Vs、Vd出现负值，可得到如下配水系统供水功能的尖点突变模型［9］:

势函数:F(V)=(V-V0)4+(Vs-Vs0)×(V-V0)2+(Vd-Vd0)×(V-V0)，

突变流形M:4(V-V0)3+2×(Vs-Vs0)×(V-V0)+(Vd-Vd0)=0，

分叉集 B:8×(Vs-Vs0)3+27×(Vd-Vd0)2=0.式中V0、Vs0、Vd0为配水系统固有的特征参数.

根据一元三次方程求根公式和盛金判别法可知，上述配水系统的分叉集方程便是配水系统尖点突变模型的稳定判据，方程4(V-V0)3+2×(Vs-Vs0)×(V-V0)+(Vd-Vd0)=0可以有1个或者3个实根，实根的数目可由判别式Δ=8×(Vs-Vs0)3+27×(Vd-Vd0)2的值来确定:(1)当Δ＜0时，配水系统位于不稳定的状态区域，有可能发生突变;(2)当Δ＞0时，配水系统控制参数的稳定变化使得状态参数V也随之稳定变化，配水系统功能是稳定的，不会发生突变;(3)当Δ=0时，配水系统处于临界平稳状态.

根据上述突变模型的分叉集方程还不能对配水系统的脆弱性进行评价，需借助归一公式对配水系统脆弱性的主次关系进行演算［10］，目的是将控制变量及状态变量的取值范围限制在［0，1］内，尖点突变模型的的归一公式为

其中:VVs，VVd分别表示灾损敏感性指数Vs、应灾能力指数Vd对配水系统整体脆弱性指数的贡献度.

2.3 配水系统脆弱性的突变评价准则

在采用突变理论对城市配水系统脆弱性进行综合评价时，需考虑“非互补”准则和“互补”准则.当主次控制变量ui对于状态变量x的贡献不可相互替代时，按照上述归一公式(2)确定状态变量x的值，要依据“非互补”的取值原则，即将突变级数值xui中的最小值作为配水系统的x值.当主次控制变量ui对于状态变量x的贡献可以互相弥补不足时，则依据“互补”的取值原则，即取各xui的平均值作为配水系统的x值.而根据上述配水系统突变模型的主、次控制变量之间关系可知，表1、2中的脆弱性评价指标之间遵循“互补”原则.

2.4 配水系统脆弱性分级标准

根据上述分析可知，配水系统整体脆弱性的大小由灾损敏感性指数Vs和人类应灾能力指数Vd共同决定，由于Vs和Vd对于V值的贡献具有相反的作用，在计算V值时，首先对Vs和Vd作同向归一处理，V值便介于［0，1］内，V值越大表示配水系统的脆弱性越高，即越容易被破坏.同时，基于以往的研究结果，根据V值的大小可确定如表3所示的配水系统脆弱性分级标准.依据上述计算的脆弱性指数V值及表3，可对城市配水系统的脆弱性等级进行评价.

表3 配水系统脆弱性分级标准

3 实例分析

3.1 研究对象

以华北某区配水系统为例，该区配水管网共56.975 km，最大管径为 DN1 000，最小管径为DN50，共包括108个节点和125根管段，管段分别用1～125表示.根据该区供水部门提供的数据统计分析可知，该区配水管道的材质种类较单一，主要是灰口铸铁管和球墨铸铁管.球墨铸铁管采用承插式楔型接头和柔性接口，灰口铸铁管采用石棉水泥刚性接头和承插式接口.该区配水管网按照不同管材、管龄、管径的累计管长及所占比例见表4～6.根据勘察资料可知，该区配水管网所在地区的地层场地属于III类土［11］，为抗震不利地段.

表4 华北某配水管网不同管材管长的统计结果

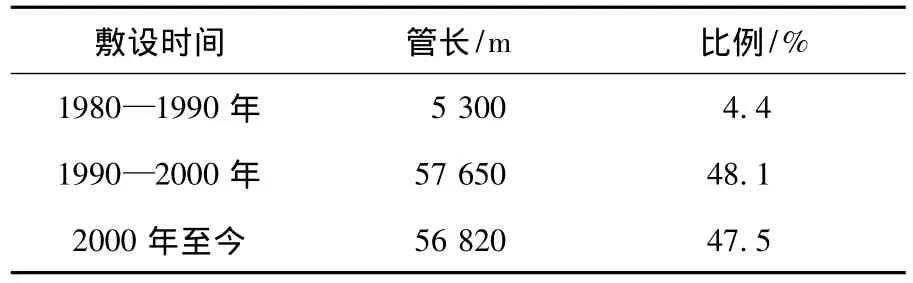
表5 华北某配水管网不同管龄管长的统计结果

表6 华北某配水管网不同管径管长的统计结果

3.2 配水系统脆弱性评价结果

根据华北某区供水管理地理信息系统统计资料可得每一根管段的管材、管径、管龄、管道连接方式，该区配水系统所处地区地层场地为III类土，同时该区为省会级城市.根据表1和2确定上述灾损敏感性评价指标及应灾能力评价指标的值，利用尖点突变模型分别计算灾损敏感性指数Vs和人类应灾能力指数Vd后，便可以根据式(2)得出该区配水系统的整体脆弱性指数V为0.1637，根据表3可知，该区配水系统的脆弱性等级为B类.

4 结语

针对配水系统面临地震威胁时其供水功能转变的突变性特征，提出一种新的城市配水系统脆弱性评价方法.首先，根据历史震害资料及配水系统抗震机理分析结果，提出配水系统脆弱性评价指标体系及分级标准;通过对配水系统状态变量及主次控制变量的确定，建立配水系统尖点突变模拟模型，并通过归一公式的导出及取值原则的确定，提出配水系统整体脆弱性指数的计算方法.应用结果表明，提出的城市配水系统脆弱性评价数学模型具有实际可行性，可作为供水管理部门进行配水系统的安全设计或改造时的决策依据.

［1］陆仁强，牛志广，张宏伟.城市供水系统风险评价研究进展［J］.给水排水，2010，36(增刊):4－8.

［2］LEE M，MCBEAN E A，GHAZALI M，et al.Fuzzy-logic modeling of risk assessment for a small drinking-water supply system ［J］.Journal of Water Resources Planning and Management，2009 135(6):547 －552.

［3］OGAWA Y，KOIKE T.Structural design of buried pipelines for severe earthquakes［J］.Soil Dynamics and Earthquake Engineering，2001，21(3):199－209.

［4］FORBES G J，HALL F L.The application of catastrophe theory in modelling freeway traffic operations［J］.Transportation Research Part A:General，1990，24(5):335－344.

［5］KNEMEYER A M，ZINN W，EROGLU C.Proactive planning for catastrophic events in supply chains ［J］.Journal of Operations Management，2009，27(2):141-153.

［6］YANG Kun，WANG Tongxu，MA Zhitao.Application of cusp catastrophe theory to reliability analysis of slopes in open－pit mines［J］.Mining Science and Technology，2010，20(1):71－75.

［7］王绍伟，王永，钱正华，等.“5.12”地震灾区供水系统受损及恢复调研与分析［J］.中国给水排水，2009，25(20):1－5.

［8］熊易华，罗万申，陈洵.汶川“5.12”地震给排水设施震损情况与启示［J］.给水排水，2009，35(10):21－24.

［9］康宇虹，徐照宇.股票价格突变模型的建立与分析［J］.哈尔滨理工大学学报，2007，12(1):100-104.

［10］BARUNIK J，VOSVRDA M.Can a stochastic cusp catastrophe model explain stock market crashes［J］.Journal of Economic Dynamics and Control，2009，33(10):1824-1836.

［11］彭艳菊，唐荣余，吕悦军，等.天津滨海场地土类别特征及其对地震动的影响［J］.地震工程与工程振动，2004，24(2):46－52.