基于正演分析的模型参数修正

张石磊，陈少峰，王焕定，王 伟

(1.哈尔滨工业大学土木工程学院，150090哈尔滨;2哈尔滨工业大学交通科学与工程学院，150090哈尔滨)

为了保证交通干线的高效运行，对架设其上的大型桥梁进行模型修正继而评定其安全性能是极其必要的.

基于正演分析的模型修正是建立包含真实结构模型及其反应的数据库，把实测反应与数据库中各个模型对应的反应进行匹配，从中寻找真实结构模型的过程［1-2］.若建立的数据库是完备的，则此数据库将包含待修正结构所有可能的状态，那么就一定包含结构的真实模型;此时，通过匹配结构反应的方式，一定可以从此数据库中找出结构的真实模型.基于正演分析的模型修正的优点和意义就在于它不需要求解反演识别方程，相应的反演识别方程的约束优化求解问题也就得以解决.已有一些利用正演模型修正思路与神经网络相结合进行的研究.Cheng Jin［3］改进了神经网络和遗传算法来推导近似极限状态函数和确定破坏概率，评估了一个悬索桥的数值模型.滕军等［4］利用支持向量机修正了有限元模型.李端有等［5］利用改进的遗传算法训练神经网络，识别了大坝的弹性模量等特性参数.费庆国等［6］利用神经网络识别了一个非线性梁模型，并进行了有限元模型修正.何浩祥等［7］利用遗传算法优化神经网络权值，修正了一个网壳结构的弹性模量.Lu Yong等［8］研究了两步模型修正法，利用频率修正模型参数.以上研究证实了基于正演分析的模型修正方法是可行的，但正演分析法亦有它的瓶颈.

假如有m个因素制约结构的模型、每个因素有n种可能的水平，那么完备的数据库将具有mn个模型［7，9］;此时正演方法需要计算 mn次以得到各种状态下结构的反应，进而为匹配响应、寻找结构的真实模型做准备.当因素和水平较多时，正演方法的计算工作量将是极其巨大的［10-13］.为了减少计算量，将均匀设计引入到基于正演的模型参数修正，构建了基于均匀设计的正演方法.

基于均匀设计的正演方法的完备性和有效性已经通过数值模拟的方式被验证，并通过模糊层次分析法评定包括振型、频率和位移等多种指标对模型修正的影响［14］.本文的目的:探索在实际结构实验信息存在不确定、不完整等因素影响下，基于均匀设计的正演方法是否仍适用.

1 静载试验数据处理

为检验基于均匀设计的正演方法，设计一个钢桁架静载试验.钢制桁架3m×0.8 m×0.5 m，模型被安装在一台500 kN压力实验机上，见图1.利用5个灵敏度为200 με/mm的数显百分表测量模型单侧下弦杆5个节点的竖向位移，位移测点编号为B1～B5.

在得到实验数据后，根据“去伪存真”的思路，剔除测量数据中的随机误差，具体步骤:

1)确定数据的基准.按照结构力学简图计算各个测点的位移，确定理论计算值与测量值之间的偏差，利用式(1)确定测量结果的基准.

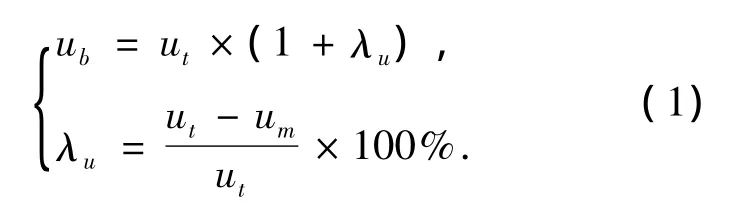
式中:ub、ut和um分别是位移的计算基准、理论计算值和实测值;λu是位移的基准调整系数.

图1 钢桁架加载示意

2)剔除随机误差.由于随机误差一般服从正态分布，误差绝对值大于3σ的概率仅为0.3%［15］.因此，令μu和σu分别为位移的均值和标准差，以［μu-3σu，μu+3σu］为取值范围，剔除不合理数据.

图2绘制了B1测点的荷载-位移曲线，图中实线为测量位移，点划线为处理后的位移.可以看出，原始记录本身就很好地满足线性和稳定性，处理后的数据与原始数据几乎重合，表明“去伪存真”后的位移记录是稳定和可靠的.

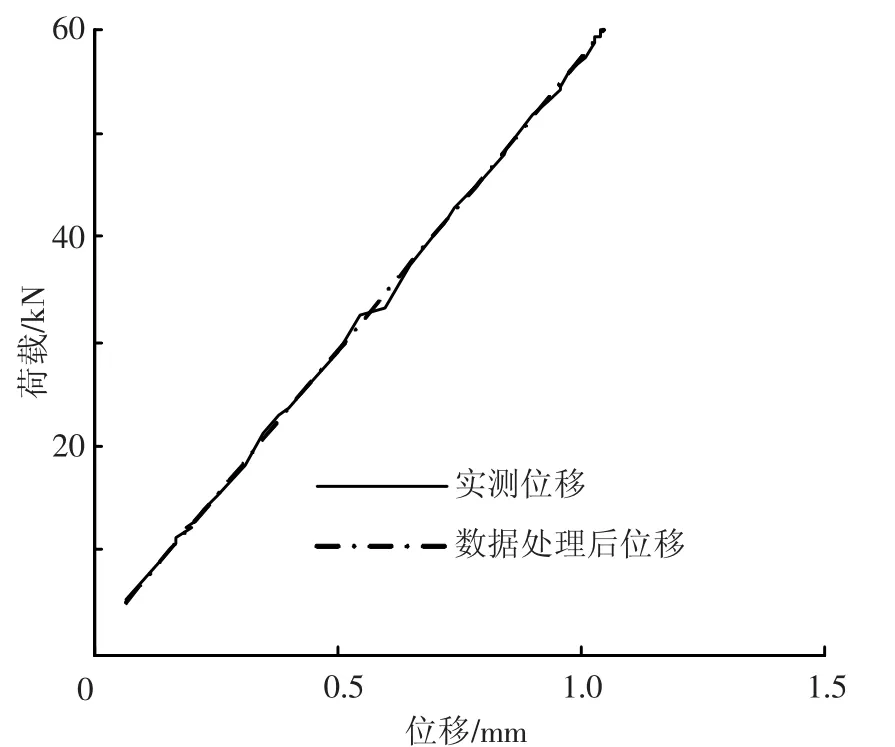
图2 B1测点位移数据处理结果

2 模型修正因素的确定

用于检验正演方法的钢桁架的节点板和对应杆件连接部位均开缝，然后用螺栓联接.当杆件受力时，由于缝隙的作用使得节点部位传递弯矩的能力下降，试图近似模拟理想桁架的力学特性.同时，为了保证节点板和对应杆件连接部位的开缝处不因较大受力而使缝隙张开，造成节点破坏，故在节点板与杆件连接部位施加轻微的角焊，具体构造见图3.

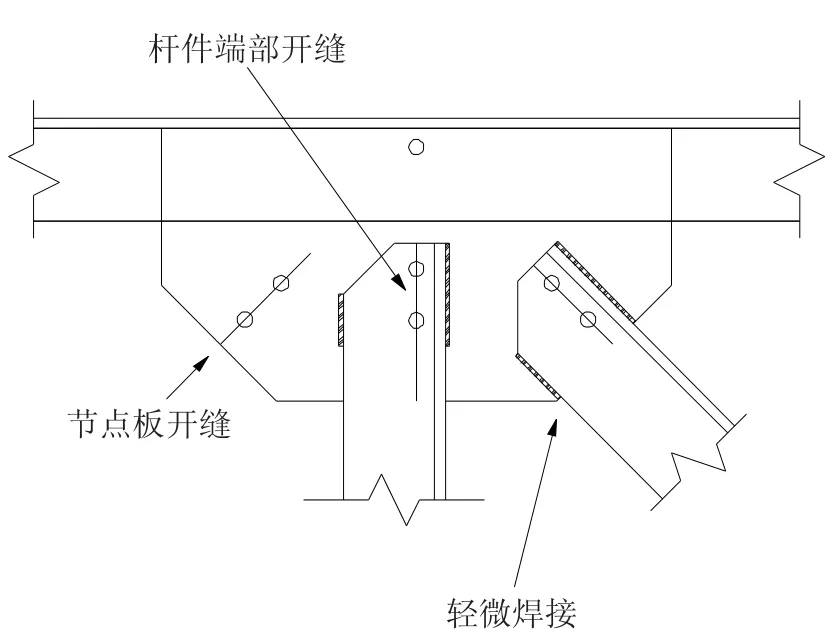
图3 模型节点构造

这种即开缝又加焊的节点，能够传递轴力，同时也能够传递一定的弯矩.以上构造导致用桁架模型和刚架模型均不能有效模拟此钢桁架.所以，将模型的节点刚度作为模型修正的主要因素.

2.1 变截面梁模拟节点力学性能

针对此模型节点的实际构造，考虑用图4的变截面梁单元来模拟节点力学性能.假设:模型的节点域对应变截面梁单元的起始段L1和终止段L3，“变截面梁单元”两端变截面部位的刚度与“待修正的节点刚度”一致，“变截面梁单元”中间段为不变截面部分.

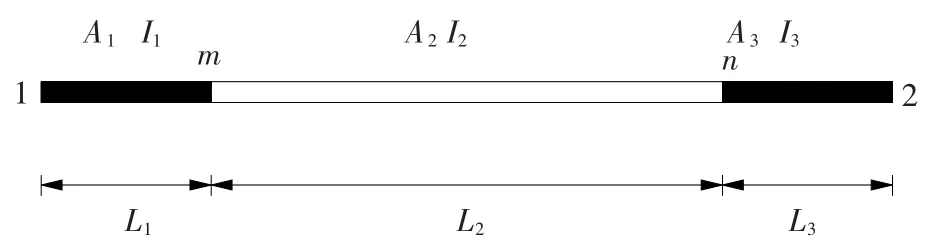
图4 变截面梁单元

“变截面梁单元”的单元刚度方程:第i子单元的单元刚度可表示为

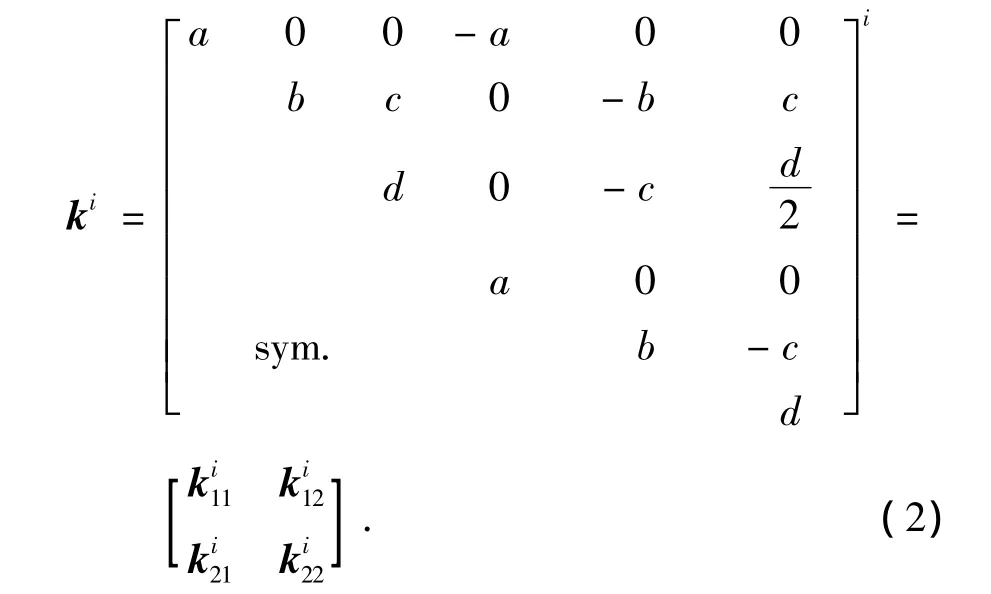
式中:a=EAi/li;b=12EIi/l3i;c= 6EIi/l2i;d=4EIi/li，(i=1，2，3).

因此上述变截面梁的总刚度方程为

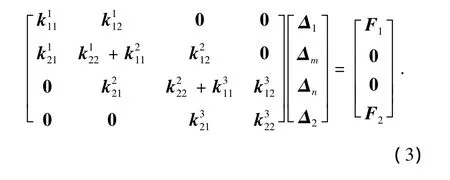
利用端节点位移表示变截面内部节点位移，并化简可得变截面杆件无梁上荷载的单元刚度方程

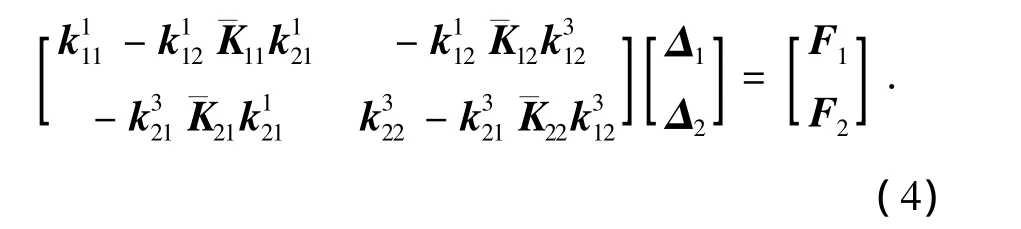
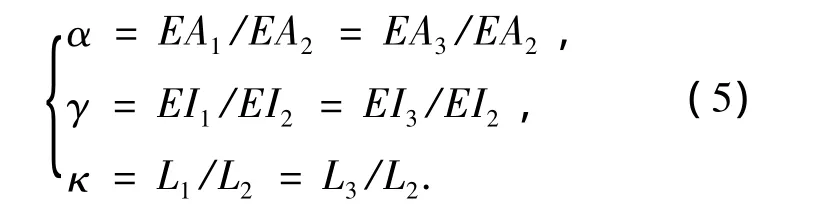
式中:α，γ，κ分别为变截面部位与不变截面部位的轴向刚度比例系数、抗弯刚度比例系数和节点作用长度比例系数.式(5)表示用变截面部位的刚度代替节点刚度，而变截面杆件的整个长度等于原来的节点域长度与实际杆件长度之和.

2.2 识别结果的区间估计

由于对实际结构进行模型修正时，一般会采集多组数据，即使没有噪声的作用，各组数据之间也会存在随机偏差.通常的处理方式是只取测量结果的均值作为模型修正的依据，但是只用均值是不能全面反映全部测量信息的，所以利用测量数据的均值和标准差求得实测结果具有95%置信概率的置信区间，然后在此置信区间内随机选取一定数量的样本作为输入，来训练Back-propagation(BP)网络，并求取对应网络输出的置信区间作为识别结果，以此来提高模型修正的准确度.

正态分布是现实世界中样本分布的最一般形式之一，土木工程结构的样本信息多数服从或近似服从这一规律［15］.故假设此模型修正的实测结果近似服从正态分布.基于概率与数理统计，令、S、μ、n分别为试验数据的均值、标准差、期望和总数，1-α为置信概率，则期望的置信区间为［16］

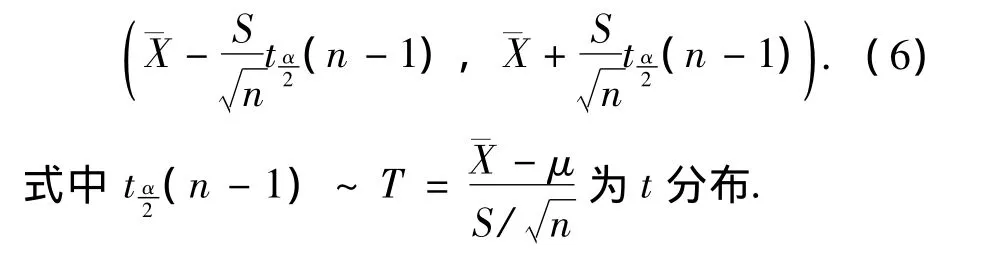
3 分步均匀设计方案修正模型参数

利用前述试验获得的数据，分别采用全因素、嵌套和分步3种均匀设计方案修正了此钢桁架模型.

3.1 分步均匀设计方案的形成

全因素均匀设计方案:把模型所有杆件对应的变截面系数均作为修正因素，建立一个大规模的均匀设计方案，非常细化地修正所有因素.其修正后的模型计算的反应与实测结果吻合非常好，但暴露出的一个问题是修正后同类杆件之间的差别较大、与实际结构不一致.分析产生这一问题的原因是均匀设计方案中各个因素是完全独立的［17］、而实际结构同类杆件之间的构造是相似的.这导致所构造的均匀设计方案中不包括接近真实情况的解，而反问题的解非唯一，通过全因素均匀设计方案得到了一个伪解.它的计算结果与实际情况非常吻合，但不是结构的真实解.

嵌套均匀设计方案:首先，把所有构件按照类型归类，用小规模均匀设计表，简要的构建各类构件、不同水平的整体均匀设计方案;然后，根据实际构造，对同类杆件的同一水平的修正因素施加适当的约束条件，使其在小范围变化，构建各个水平的细化方案;最后，把各个水平的细化方案嵌套在整体均匀设计方案之中，形成嵌套均匀设计方案.这样做实际是把小规模的均匀设计方案嵌套在整体方案的各个水平之内，实现与大规模均匀设计方案相同的作用，而约束条件将限制同类杆件相同因素之间的差异，使得修正结果趋于合理.计算结果显示此方案比全因素均匀设计方案得到的结果更合理，但依旧存在同类杆件之间留有一定差异的现象.分析其原因为嵌套方案只约束了同一个水平的杆件特性，没有约束各个水平间的差异.所以，导致结果依旧不完全合理.针对以上问题，最后采用了分步均匀设计方案.

分步均匀设计方案:根据结构特点，确定影响结构各因素的重要性依次为轴向刚度、抗弯刚度、节点作用范围.把杆件按照类型归类，用小规模均匀设计表分两步修正模型.第一步利用位移作为人工神经网络的输入参数，主要修正各类杆件的轴向刚度、附带修正其他次要因素;各参数的初始取值区间为α∈［0.8，1.2］、γ∈［0.8，1.2］、κ∈［0.18，0.22］.选取均匀设计表 U*29(296)的第1、3、4列安排均匀设计方案，此均匀设计方案的偏差为0.0914;然后利用U*4(44)交换各因素的排列位置，拓展均匀设计方案试验次数为116.并建立了一个三层BP神经网络，其输入层神经元数为5，隐含层神经元数为11，输出层神经元数为3;利用含有动量项的最速下降算法训练神经网络的权值，训练目标误差为0.001，最大迭代次数为10000.神经网络整个训练过程的均方误差绘制于图5中，神经网络在第271次迭代收敛.最后，利用式(6)确定实测位移的置信区间，并从中随机抽取45组样本，输入训练好的神经网络，得到45组结构参数的预测值，并取45组参数预测结果的平均值作为第一步模型修正的最终结果.第一步模型修正的最终结果是α=0.9074、γ=0.883 0、κ=0.194 1.

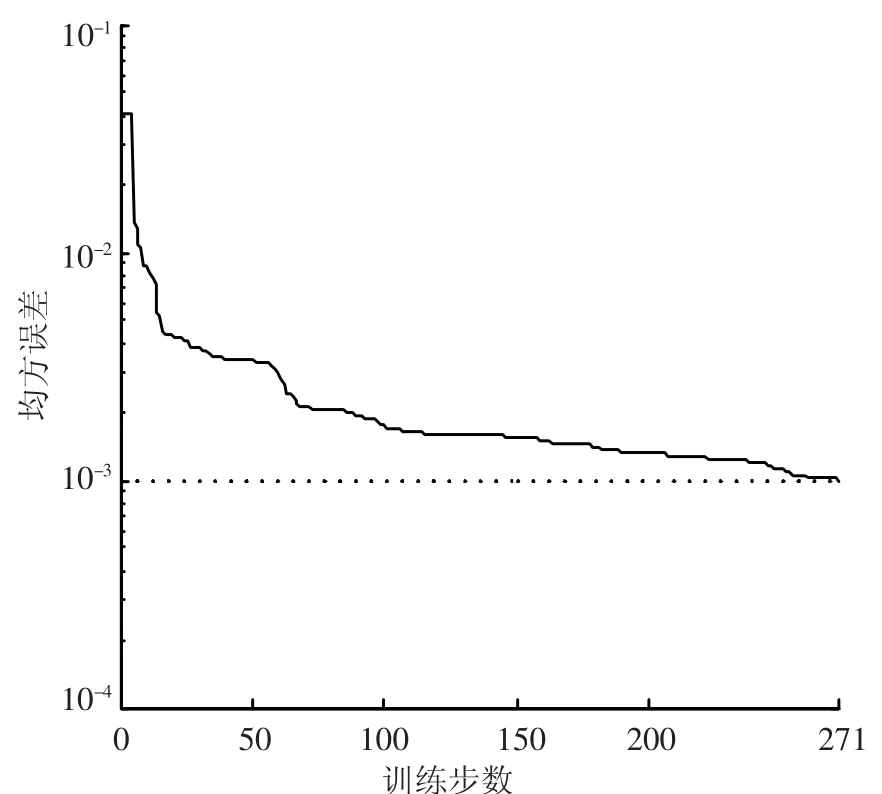
图5 第一步模型修正训练误差曲线

在第二步修正方案中，考虑修正因素之间的约束关系，令各类杆件的变截面比例系数在第一级修正基础上做适当变化，修正因素调整为第一级与第二级修正的变截面比例系数的比值c1～c12，其中

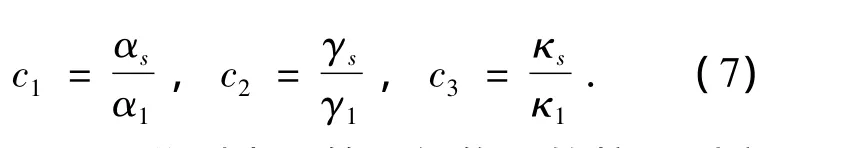
式中:α1，γ1，κ1分别表示第一级修正的抗压刚度比例系数、抗弯刚度比例系数和节点作用域长度比例系数的修正结果，s表示杆件类型为上弦杆，c1～c3为上弦杆的前后两次修正结果的比值.

根据结构的实际构造，确定修正因素的初始取值区间为 c1∈［1.0，1.2］、c2∈［1.0，1.2］、c3∈［0.9，1.1］，其他的9个比值c4～c12的意义和取值方法与c1～c3相似.同时，利用自制的均匀设计表U*24(2412)建立均匀设计方案，再次按照第一级修正中相同的方式修正各个因素.第二级模型修正中神经网络的均方误差绘制于图6中，按照均匀设计方案训练的神经网络在第5808次迭代时收敛.表1给出了第二步模型修正的结果.

表1 c1～c12的修正结果

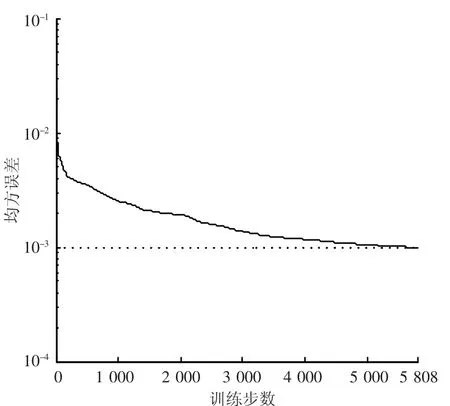
图6 第二步模型修正训练误差曲线

3.2 模型修正结果

分布均匀设计方案的最终修正结果示于表2和表3.从修正结果看，上弦杆和下弦杆的变截面轴向刚度和抗弯刚度均大于1，表明弦杆的节点区域的刚度大于非节点区域;竖腹杆和斜腹杆的变截面轴向刚度和抗弯刚度均小于1，这与实际模型节点部位开缝的构造相吻合;弦杆和腹杆的节点域长度系数为0.2～0.25，与实际模型节点的尺寸趋于一致.

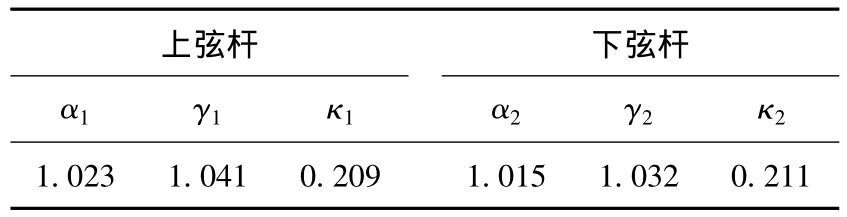
表2 弦杆修正结果

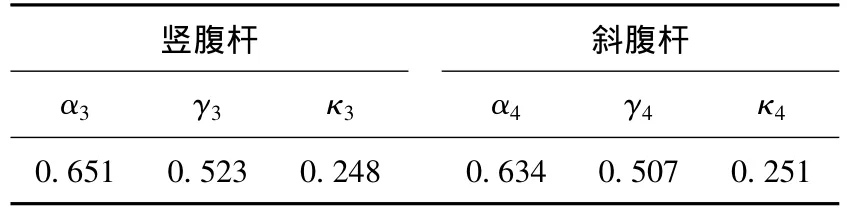
表3 腹杆修正结果

为了验证模型修正结果，计算了修正后模型跨中承受60 kN集中力时各个测点的挠度，与实测结果进行比较示于图7(a).图7(a)显示修正后模型的计算结果明显优于修正前的，它更加接近真实值.为了进一步确定模型修正结果的正确性，又测量了模型在三分点对称加载工况下的节点挠度，并再次比较修正前后的挠度，结果示于图7(b).结果显示:改变加载工况后修正结果和实测结果保持一致，即本次模型修正结果是可靠的.

3.3 基于均匀设计的正演方法向复杂结构的推广

实际需要修正的工程项目通常为大尺度的复杂空间结构.前述研究的对象是小型的桁架，它与复杂结构之间的模型修正有区别.复杂结构较之小型结构模型修正之间的最大区别是待修正因素的种类更多和数量更庞大.当待修正因素规模众多时，第一个困难是建立大规模均匀设计方案.现有可以获得的均匀设计表，可修正的因素的规模不超过50.笔者曾经研制了大规模的均匀设计表及其使用表，并采用中心化L2偏差度量均匀设计的好坏.在第3节建立的全因素方案就是基于大规模均匀设计表制定的.但是大规模的均匀设计方案不一定能够得到好的结果，因为均匀设计各个因素之间是独立的、充分均匀分散的，而实际结构的修正因素之间是有约束关系的，第3节的计算也证明了这一点.

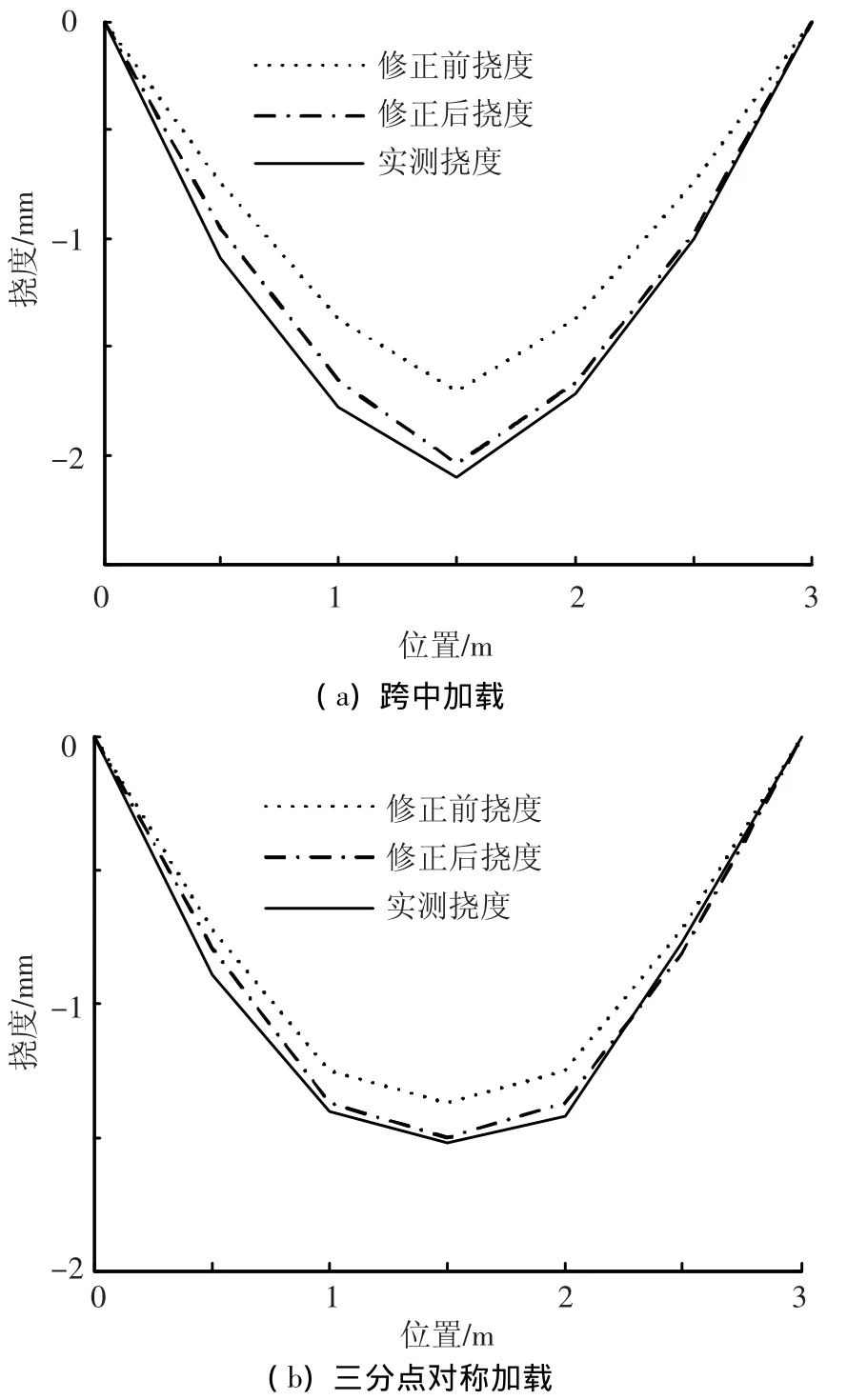
图7 修正前后挠度比较

复杂结构的模型修正不单单是修正因素增加了，它需要修正的因素类型也扩大了.模型修正实际上包含修正两大类因素:设计参数和刚度、阻尼、质量矩阵中的元素.复杂结构的力学模型不准确的原因:可能为设计参数不准确;也可能为力学假设、简化建模和边界条件不清楚导致力学模型中的矩阵元素不正确造成的.在多数情况下，只修正设计参数或者只修正矩阵元素是不能达到模型修正要求的.把主因素分析、分步修正和优选法［18］融入到基于均匀设计的正演分析法是一条可行的道路.假设大型复杂结构的设计参数为p、刚度矩阵为K.ω和u为有限元模型的计算频率和变形;和为结构的测量频率和实际变形.

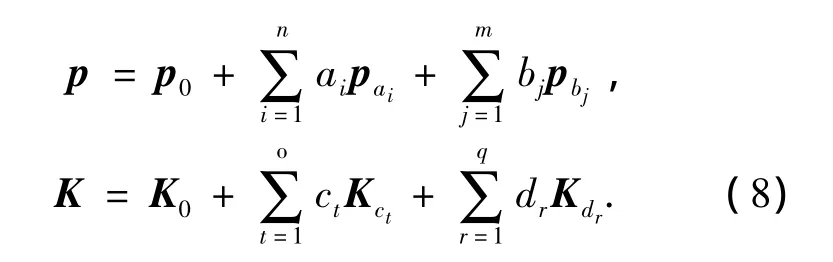
式中:ai、bj、ct和 dr为待修正的因素;p0和 K0为初始的设计参数和刚度矩阵;pai和Kct是待修正因素发生单位变化时相应的设计参数和刚度矩阵的敏感性矩阵;pbj和Kdr为前一步模型修正结果与后一步模型修正结果之间的差值矩阵.

1)首先，利用摄动法确定 ai、bj、ct和 dr的重要性顺序，即确定主要因素.

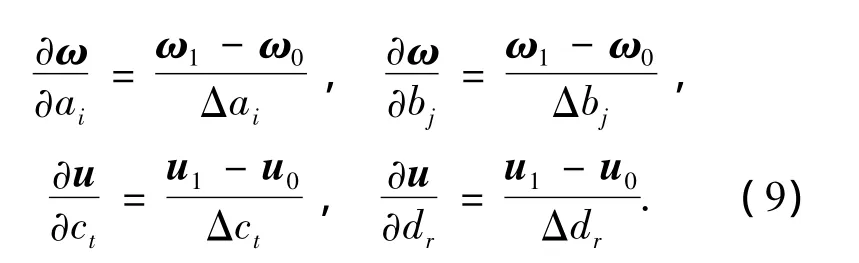
具体计算方法是按照式(9)使以上因素发生摄动，求取频率和变形的变化率，变化率大者为主因素.

2)按照上述求得的因素重要性次序，依次建立小规模的均匀设计方案.在因素的取值上，应考虑结构的实际构造加以适当的约束;同时因素的取值范围应尽量大以便覆盖待修正因素的真实解;然后分多步修正各个因素.

3)在每一步模型修正中，在实测频率和变形的置信区间内，随机抽取一定数量的样本输入训练好的神经网络，辨识多组结果，并求取它们的平均值作为本步的修正结果.

4)当所有的因素均修正完毕之后，比较修正的精度是否满足要求.如果不满足要求，则重复1)～3)步骤，直至满足精度为止.

5)当复杂结构需要修正的因素特别多的时候，应该采用优选法里固定次要因素，按照1)～4)的步骤只修正最主要的因素.当第一主因素修正完毕之后，再修正第二主因素，逐个因素轮换修正，最终达到修正复杂结构有限元模型的目的.

4 结语

当合理地确定了模型修正因素和水平后，本文所提出的基于均匀设计的正演分析方法可以克服测量信息不确定、不完整等因素的影响，能够修正模型参数.即，在实际结构的模型修正中应考虑修正因素的相关性，采用分步均匀设计方案修正模型参数.

［1］张德文，魏阜旋.模型修正与破损诊断［M］.北京:科学出版社，1999:1-2.

［2］CHANG C C，CHANG T Y P，XU Y G，et al.Selection of training samples for model updating using neural networks［J］.Journal of Sound and Vibration，2002，249(5):867-883.

［3］CHENG Jin.An artificial neural network based genetic algorithm for estimating the reliability of long span suspension bridges［J］.Finite Elements in Analysis and Design，2010，46(8):658-667.

［4］滕军，朱焰煌，卢云军，等.基于多输出支持向量回归机的有限元模型修正［J］.振动与冲击，2010，29(3):9-12，47.

［5］李端有，甘孝清，周武.基于均匀设计与遗传神经网络的大坝力学参数反分析方法［J］.岩土工程学报，2007，29(1):125-130.

［6］费庆国，李爱群，张令弥.基于神经网络的非线性结构有限元模型修正研究［J］.宇航学报，2005，26(3):267-269，281.

［7］何浩祥，闫维明，王卓.基于子结构和遗传神经网络的递推模型修正方法［J］.工程力学，2008，25(4):99-105.

［8］LU Yong，TU Zhenguo.A two-level neural network approach for dynamic FE model updating including damping［J］.Journal of Sound and Vibration，2004，275(3/4/5):931-952.

［9］ATALLA M J，INMAN D J.On model updating using neural networks［J］.Mechanical Systems and Signal Processing，1998，12(1):135-161.

［10］UNGER J F，KÖNKE C.An inverse parameter identification procedure assessing the quality of the estimates using Bayesian neural networks［J］.Applied Soft Computing，2011，11(4):3357-3367.

［11］朱劲松，肖汝诚.大跨度PC斜拉桥结构快速分析神经网络模型［J］.中国铁道科学，2007，28(1):33-39.

［12］SAATY T L，VARGAS L G.Estimating technological coefficients by the analytic hierarchy process［J］.Socio-Economic Planning Sciences，1979，13(6):333-336.

［13］ZADEH L A.Fuzzy sets［J］.Information and Control，1965，8(3):338-353.

［14］ZHANG Shilei，CHEN Shaofeng，WANG Huanding，et al.Evaluating identification indices on damage detection by a fuzzy analytical hierarchy process［C］//2011 International Conference on Structures and Building Materials.Guangzhou:TTP，2011:2934-2940.

［15］姚振纲，刘祖华.建筑结构试验［M］.上海:同济大学出版社，2009:252-253.

［16］罗敏娜.概率论与数理统计［M］.北京:科学出版社，2008:153-156.

［17］QIN Hong，ZHANG Shangli，FANG Kaitai.Constructing uniform designs with two-or three-level［J］.Acta Mathematica Scientia，2006，26 B(3):451-459.

［18］华罗庚.优选法平话及其补充［M］.北京:国防工业出版社，1971:9-11.