山岭隧道水压力分布对围岩稳定性及结构受力影响研究

高新强，刘志春，韩现民

(石家庄铁道大学土木工程学院，河北石家庄 050043)

山岭隧道水压力分布对围岩稳定性及结构受力影响研究

高新强，刘志春，韩现民

(石家庄铁道大学土木工程学院，河北石家庄 050043)

采用平面有限元数值模型分析透水衬砌、排水系统和墙脚排水3种排水形式下，无水压、衬砌水压力在均布和非均布时蛋形断面和圆形断面山岭隧道围岩的稳定性及结构受力特征。研究了衬砌水压力不同分布对隧道位移、塑性区和结构受力的影响规律，并对衬砌水压均布与非均布的结果进行了对比分析。分析结果表明:水压力的存在使隧道位移、塑性区范围和塑性应变最大值显著增加，对围岩的稳定性不利，特别是对结构受力的影响更加显著。水压力较大时，从围岩稳定性和结构受力来讲采用圆形断面优于蛋形断面。水压力不均匀分布时对围岩稳定性和结构受力均产生不利影响。

山岭隧道 均布水压 非均布水压 围岩稳定性 结构受力

国内外隧道工程中由于地下水的涌出和水压力对围岩稳定性和结构产生破坏性影响的实例屡见不鲜。如圆梁山隧道[1]过高的水头压力和大量涌水直接威胁施工人员、设备的安全及隧道衬砌结构的可靠性，施工进入高压富水区段时，遭遇了多次突发性、大规模的高压涌(突)水、突泥(含泥量达到50%以上)。日本东海道干线旧丹那隧道[2](长7.84 km)，最大的一次断层涌(突)水量达2.85×105m3/d，水压高达1.4～4.2 MPa。隧道的涌水、突泥严重影响了施工进度和周围环境。部分隧道运营后由于高水压而导致衬砌开裂破坏[3]。因此，高水压富水区隧道围岩的稳定性、地下涌(突)水和衬砌水压力是关系到高水压富水区隧道能否修建成功的关键。

1 工程背景

以渝(重庆)怀(怀化)铁路圆梁山深埋特长隧道毛坝向斜段为工程背景，隧道总长11.068 km，隧道最大埋深为780 m。隧道地质条件异常复杂，主要地质构造为毛坝向斜和桐麻岭背斜及其伴生或次生断裂等构造。高水压力问题是该隧道遇到的主要工程地质问题之一[4]。隧道毛坝向斜段属于高水压富水区，水头高度为450 m，静止水压为4.5 MPa。研究分析注浆圈和衬砌上水压力的大小及分布对隧道围岩稳定性和衬砌结构受力的影响及其规律，对高水压富水区隧道的设计和施工具有重要的应用价值。

2 水压力确定方法

2.1 水从衬砌渗流进隧道时

将作用在衬砌内的水荷载等效成作用在衬砌外表面的水压力荷载。由图1可以得到作用在衬砌外表面的等效水压力荷载Fl为

式中，r1为衬砌内半径;rl为衬砌外半径;Pl为衬砌背后水压力;P1为衬砌内表面水压力(铁路、公路隧道取0，水工引水隧道取内水压力)。

将作用在注浆圈内的水荷载等效为作用在注浆圈外表面的等效水压力荷载，由图1可以得到作用在注浆圈外表面的等效水压力荷载Fg为

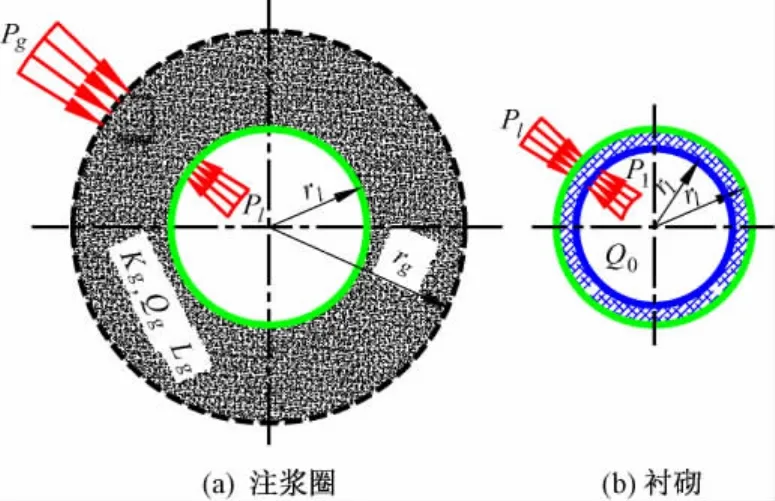
图1 水压力荷载计算图示

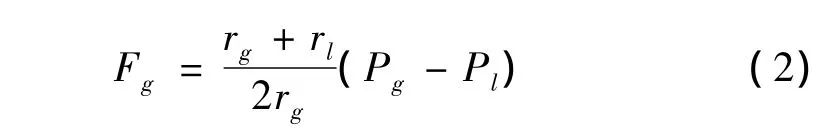
式中，rg为注浆圈半径;Pg为注浆圈外表面水压力。

2.2 水通过衬砌背后的排水系统排出时

Pl值采用模型试验[1]的结果。

作用在注浆圈外表面的等效水压力荷载采仍用式(2)计算。

当衬砌断面为蛋形时，采用等效半径进行近似计算。

3 计算工况

根据水压力作用系数、隧道模拟排水形式、隧道控制排水量、衬砌断面形式进行组合，分7种工况计算，工况的划分见表1。工况3，工况6分别为蛋形断面和圆形断面无水时的情况，用于计算结果的比较分析。

圆梁山隧道高水压段采用3～8 m的注浆圈堵水，注浆的主要目的是减小注浆圈内围岩的渗透系数。以注浆圈厚度5 m为例进行计算分析，其他注浆圈厚度可参照此方法进行[5]。

作用在注浆圈外表面和衬砌外表面的等效水压力荷载见表1[1]。表中，工况7衬砌上等效水压力荷载为平均值，参照试验得出的水压力施加[1]，如图2所示。其余等效水压力荷载在断面上按均匀分布施加。

图2 工况7衬砌外表面施加的水压力分布(单位:MPa)

表1 平面有限元计算工况及等效水压力荷载取值

4 计算模型和计算参数

有限元计算分析采用大型商用有限元软件ANSYS进行，分析模型采用弹塑性平面应变模型，围岩(包括注浆圈部分)采用弹塑性材料模拟，屈服准则采用Drucker-Prager准则，衬砌采用弹性梁单元进行模拟。有限元分析模型和网格划分如图3所示。根据圆梁山隧道工程地质勘测报告[4]和铁路隧道设计规范[6]，隧道围岩主要为Ⅱ级围岩(灰岩为主)，因地下水丰富，地下水会降低围岩的黏聚力、内摩擦角和弹性模量，因此黏聚力、内摩擦角和弹性模量按围岩稳定性低一级即Ⅲ级围岩选取。隧道衬砌结构按设计的C40钢筋混凝土(蛋形断面)，C30-X型钢混凝土(圆形断面)参数选取。注浆圈的计算参数通过提高(提高10%)围岩的变形模量E值来模拟，注浆圈的黏聚力和内摩擦角分别采用1.2 MPa和45°，注浆圈厚度为5 m。具体计算参数见表2。

图3 有限元分析模型和网格划分

表2 围岩和衬砌计算参数

边界条件:模型下边界上施加法向位移约束(Y方向位移等于0)，下边界中间点约束X方向位移。左右边界和上边界按地质勘查报告分别施加14.45 MPa，15.78 MPa初始地应力。

隧道开挖方式为全断面开挖，开挖模拟是通过杀死开挖部分的单元实现的，即把死单元相关的刚度和荷载变为一小值(如1×10-6)。衬砌施作通过激活单元和改变材料属性来实现，水压力按等效节点荷载大小施加在衬砌和注浆圈周边节点上。

5 计算结果与分析

工况1～工况7隧道位移、塑性应变最大值见表3，衬砌内力最大值见表4。

表3 各工况下隧道位移、塑性应变最大值

表4 各工况下衬砌内力最大值

5.1 有水压与无水压时的比较

采用蛋形断面时，有无水压隧道的位移和衬砌内力分布形状相似、最大值位置相同，只是数值不同。以工况3(无水压)为基准，将工况1(透水衬砌)和工况2(排水系统)与工况3比较，结果见表5。

采用圆形断面时，有无水压隧道的位移和衬砌内力分布形状相似、最大值位置相同，只是数值不同。以工况6(无水压)为基准，将工况4(透水衬砌)、工况5(排水系统)和工况7(墙脚排水)与工况6比较，结果见表6。

表5 蛋形断面有水压与无水压比较结果

表6 圆形断面有水压与无水压比较结果

由表5和表6可以看出:水压力的存在使隧道位移增加，塑性区加大，对隧道的稳定性是不利的，特别是对结构受力(轴力、弯矩和剪力)的影响更加显著。

5.2 衬砌渗出与排水系统排出的比较

采用蛋形断面时，以工况1(透水衬砌)为基准，将工况2(排水系统)与工况1比较;采用圆形断面时，以工况4(透水衬砌)为基准，将工况5(排水系统)与工况4比较。结果见表7。

表7 衬砌渗出与排水系统排出的比较结果 %

由表7可以看出:水压力作用系数相同时，地下水从衬砌背后的排水系统排出时，隧道位移、塑性应变、衬砌内力的最大值比从衬砌渗出时要稍大，但增加量非常小，所以得到水压力作用系数后用两种情况计算均可。

5.3 蛋形断面与圆形断面的比较

水从衬砌渗出时，以工况4(圆形断面)为基准，将工况1(蛋形断面)与工况4比较;水通过衬砌背后的排水系统排出时，以工况5(圆形断面)为基准，将工况2(蛋形断面)与工况5比较，结果见表8。

表8 蛋形断面与圆形断面的比较结果 %

由表8可以看出:水压力作用系数相同时，蛋形断面比圆形断面隧道竖向位移、位移矢量、衬砌轴力最大值有所减小(15% ～40%)，主要是由于采用圆形断面时为满足隧道限界要求，开挖断面积比蛋形断面积大所致。但是，蛋形断面比圆形断面隧道水平方向位移、塑性应变、衬砌弯矩、剪力最大值都要增加，塑性区范围增大约0.3 m，塑性应变明显增大，特别是弯矩和剪力增加很显著。另外，蛋形断面最大弯矩部位，轴力较小，引起截面偏心矩增大，会对结构受力产生显著的不利影响。因此水压力较大时，从围岩稳定性和结构受力来讲采用圆形断面优于蛋形断面。

5.4 水压不均匀分布与均匀分布比较

衬砌背后盲管排水系统局部堵塞后，可能造成衬砌背后水压力分布不均匀，以工况4(水压均匀分布)为基准，将工况7(水压不均匀分布)与工况4比较，结果见表9。

表9 水压不均匀分布与均匀分布比较结果 %

由表9可以看出:水压力不均匀分布比均匀分布隧道位移、塑性应变、衬砌内力的最大值都要增加，特别是塑性应变和弯矩的最大值增加很显著，水压不均匀分布时塑性区宽度增加约0.1 m。另外，水压不均匀分布时弯矩最大值位置的轴力还较小，引起截面偏心矩增加，对结构受力不利。因此水压力不均匀分布时对围岩稳定性和结构受力均产生不利影响。

6 结论

1)衬砌水压力的存在使隧道位移增加，塑性区加大，对隧道围岩的稳定性不利，特别是对结构受力(轴力、弯矩和剪力)影响更加显著。

2)衬砌水压力作用系数相同时，地下水通过衬砌背后的排水系统排出时，隧道位移、塑性应变、衬砌内力的最大值比从衬砌渗出时要稍大，但增加量很小，所以得到水压力作用系数后用两种情况计算均可。

3)衬砌水压力较大时，从围岩稳定性和结构受力来讲采用圆形断面优于蛋形断面。

4)水压力不均匀分布时对围岩稳定性和结构受力均产生不利影响。

5)高水压隧道衬砌截面上的轴力、弯矩和剪力都很大，因此建议当衬砌上的水压力＞3.0 MPa时，必须进行排水或增大隧道的控制排水量。

[1]高新强.高水压山岭隧道衬砌水压力分布规律研究[D].成都:西南交通大学，2005.

[2]王建秀，朱合华，叶伟民.隧道涌水量预测及工程应用[J].岩石力学与工程学报，2004，23(7):1150-1153.

[3]代峪.云雾山隧道突泥灾害工程地质特征与防治[J].铁道建筑，2009(10):33-35.

[4]铁道第二勘测设计院.圆梁山深埋特长隧道工程地质勘测报告[R].成都:铁道第二勘测设计院，2000.

[5]高新强，仇文革，高杨.山岭隧道高水压下衬砌结构平面数值分析[J].岩土力学，2005，26(3):365-369.

[6]中华人民共和国铁道部.TB 10003—2001 铁路隧道设计规范[S].北京:中国铁道出版社，2001.

U451

A

1003-1995(2012)06-0074-04

2012-01-10;

2012-03-14

铁道部科技发展计划项目(2001G009-2);河北省自然科学基金项目(E2010001060);石家庄铁道大学土木工程学院基金项目(52704706)

高新强(1970— )，男，山东邹平人，副教授，博士。

(责任审编 葛全红)