均匀分布的区间估计方法及应用

徐晓岭，朱灵芝

（1.上海对外贸易学院 商务信息学院，上海 200234；2上海师范大学 数理学院，上海 200234）

均匀分布的区间估计方法及应用

徐晓岭1，朱灵芝2

（1.上海对外贸易学院 商务信息学院，上海 200234；2上海师范大学 数理学院，上海 200234）

文章给出了均匀分布在全样本场合下参数的三种区间估计方法，通过大量Monte-Carlo模拟考察了各种区间估计方法的精度，并通过实例说明了这些区间估计方法的应用。

均匀分布；全样本；区间估计；MonteCarlo模拟

设总体X服从区间[θ1,θ2]上的均匀分布，记为X～U[θ1,θ2]，X1,X2,…,Xn为来自X的一个样本，可以证明：θ1，θ2的极大似然估计分别是：=X(1)，=X(n)，其中X(1)，X(n)分别为最小和最大次序统计量。

1 全样本场合下参数θ1,θ2的区间估计

设 X1,X2,…,Xn为来自总体X～U[θ1,θ2]的容量为n的一个简单随机样本，X(1)≤X(2)≤…≤X(n)为其次序统计量。下面通过三种方法来求参数θ1,θ2的置信水平1-α的区间估计。

为考察全样本场合下上述三种区间估计方法的优劣，给定样本容量n=10(5)30，参数真值θ1=2,θ2=5，置信水平为1-α=0.95，通过1000次Monte-Carlo模拟得到参数θ1,θ2的区间估计的平均下限、平均上限、平均区间长度和包含参数真值的个数，结果列于表1、表2、可以看到，从平均区间长度来看，方法一较好。

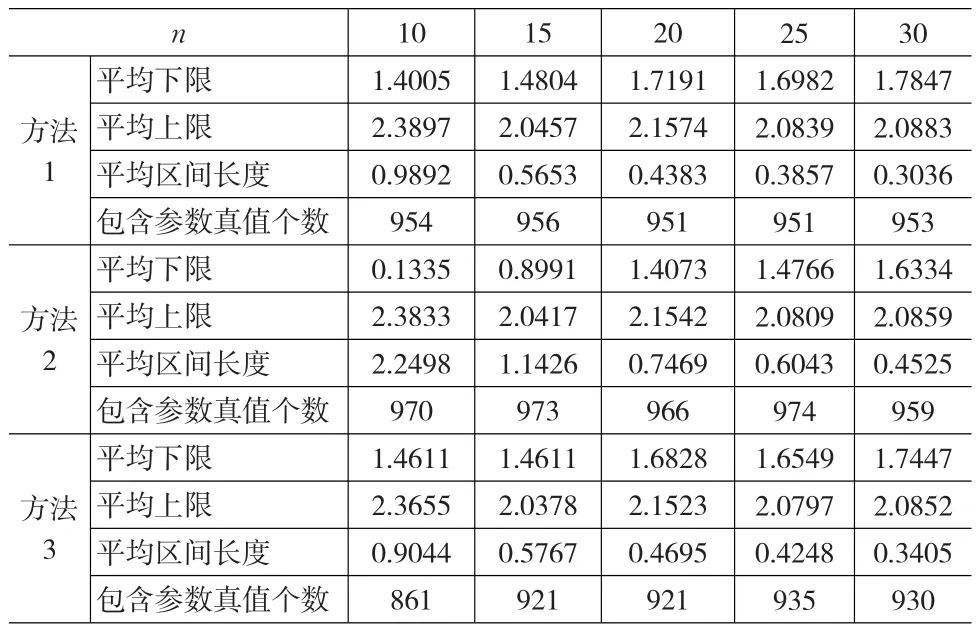
表1 全样本场合下参数θ1的区间估计的模拟结果

表2 全样本场合下参数θ2的区间估计的模拟结果

例：给定样本容量为n=20，参数真值为θ1=6,θ2=8，通过Monte-Carlo模拟产生一组服从均匀分布的随机样本：7.5048,6.9629,6.8739,7.1731,7.1797,7.3868,7.2132,7.1207,7.9245,6.4690,6.6101,6.3016,7.0824,6.7201,6.3803,6.7344,7.8960,7.3130,7.5301,6.0425.

在全样本场合下，利用本文三种区间估计方法可得：参数θ1的置信水平为95%的区间估计分别为：方法1[5.7210,6.0425]，方法 2[5.4924,6.0401]，方法 3[5.6944,6.0387]；参数θ2的置信水平为95%的区间估计分别为：方法1[7.9245,8.2459]，方法 2[7.5813,9.0208]，方法3[7.9269,8.4745]，其中方法一的区间长度最短。

2 结论

在全样本场合下，从平均区间长度来看，本文所给出的均匀分布的参数θ1,θ2的三种区间估计方法中，方法一精度最高。

[1]E.L.Lehmann.Elements of Large-sample Theory[M].New York：Spring er,2010.

[2]王秀丽.均匀分布参数的最短置信区间[J].数学的实践与认识，2008，（9）.

[3]顾蓓青,徐晓岭.关于均匀分布统计分析的一些思考[J].统计与信息论坛，2010，（12）.

O212

A

1002-6487（2012）24-0023-03

国家自然科学基金资助项目（11141002）；上海对外贸易学院085重点学科专业建设项目；上海市星系与宇宙学半解析研究重点实验室项目（SKLA1101）

徐晓岭（1965-），男，江苏宜兴人，博士，教授，研究方向：可靠性统计。

朱灵芝（1985-），女，湖北枝江人，硕士研究生，研究方向：可靠性统计。

（责任编辑/亦 民）