基于独立特征提取的MPCA方法在人脸识别中的应用
张锦华
(周口师范学院 计算机科学与技术学院,河南 周口 466001)
基于独立特征提取的MPCA方法在人脸识别中的应用
张锦华
(周口师范学院 计算机科学与技术学院,河南 周口 466001)
为了弥补传统MPCA(ModularPrincipalComponentAnalysis)方法在人脸识别中忽略子图像之间差异的缺陷,本文提出了一种基于独立特征提取的MPCA方法(ModularPCABasedonIndependentFeature,IFMPCA).首先选取人脸训练样本中具有相似光照、表情和姿态的图像进行分块,然后将训练样本的子图像和测试样本的子图像进行最优投影,得到子特征矩阵.最后,求得样本间的距离,利用最小距离分类器进行样本的分类.在Yale人脸数据库上的实验结果表明:IFMPCA算法在人脸正确识别率方面优于传统PCA算法.
MPCA;IFMPCA;人脸识别;独立特征提取
人脸识别作为生物识别的重要组成部分,在智能人机交互、身份鉴别、身份证明、刑侦破案和安全监控等方面有着广泛的应用[1],同时,它也是模式识别领域中较为典型的多类型判断问题.在人脸识别的众多方法中,基于特征脸的PCA方法(PrincipalComponentsAnalysis,主成分分析方法)又称为K-L变换,是目前主流也是最为成功的线性鉴别分析方法之一[2].从本质上来说,PCA方法是图像压缩的一种最优正交变换,用低维子空间来描述人脸特征,实现在最小均方意义下寻找最能代表原始人脸数据的投影[3].需将人脸图像矩阵预处理为一维向量,然后以此向量为人脸原始特征进行识别.但是,该方法在对人脸数据进行降低维度处理之后,仍然存在大量的冗余信息,严重影响了PCA方法的效率.另外,由于PCA以全局方式抽取人脸特征,识别过程易受到光照、表情和姿态等因素的影响[4].实际上,当光照、表情和姿态变化时,人脸仅部分区域变化明显,因此采用分块的方法对图像进行鉴别分析可以有效捕捉人脸局部特征信息,有利于提高人脸识别的效度和精度[5].
陈伏兵[6]等人提出了一种分块的PCA方法,即MPCA方法.这种方法首先根据图像中人脸表情和光照等基本参数对图像进行分块,然后对子图像利用PCA方法进行线性鉴别分析.MPCA方法的优点是能够充分考虑图像的局部特征.但缺点是使用同一个投影矩阵对分块后的图像进行投影,未考虑测试样本子图像和训练样本子图像之间的差异.
为了提高传统MPCA算法的人脸识别性能,本文在以上方法的基础上提出基于独立特征提取的MPCA算法.首先,从原有数字图像模式出发,将所有人脸图像训练样本按照光照、表情和姿态进行划分,使各个子模块更接近高斯分布.然后,充分考虑训练样本子图像和测试样本子图像之间的差异,求出子模块图像的散布矩阵和最优投影矩阵,通过投影得到子模块图像的独立特征矩阵.最后,利用最小距离分类器进行测试样本的分类.在著名的Yale人脸数据库上的实验结果表明:IFMPCA算法在识别性能上优于传统的MPCA算法.
1 PCA的基本原理
1.1 PCA人脸识别方法
主成分分析法(PrincipalComponentsAnalysis,PCA)是由M.Turk和A.Pentland提出的一种基于特征点的人脸识别方法.将PCA方法应用于人脸识别,其前提是假设处理的人脸位于低维线性空间,且不同的人脸具有可分性.该方法的基本原理是首先将人脸看成一个整体,借助正交变换,将人脸相关的P个随机向量转化成分量不相关的K个(K≤P)随机向量,实现高维向量到低维向量的转换,形成低维线性特征子空间[7].识别人脸时,将单张人脸图像投影到此低维空间,用所得投影坐标系数与目标样本集中的投影系数进行比对,以确定最佳特征脸.
PCA人脸识别步骤主要包括:
(1)人脸图像进行几何归一、光照补偿等预处理.
(2)读入特定人脸数据库,将人脸样本形成特征空间.
(3)将训练样本图像和测试人脸图像进行正交变换、投影等步骤.
(4)选择合适分类方法判断训练样本和测试人脸是否同类.
1.2 PCA人脸识别具体流程
从本质上来说,PCA方法是在最小均方下查找最能代表原始数据的投影方向,从而达到对特征空间降低维度的目的.PCA假设每张人脸图像Ri由n=k×l个像素组成,则此人脸图像可以构成一个k×l的矩阵,矩阵向量化后表示为
选择相似光照、表情和姿态的部分将人脸训练样本分为S类,第i类有m个人脸图像样本,组成的训练矩阵为:
X=[x11,x12,…,xij]T,i∈1,2,…,s,j∈1,2,…,m
根据平均脸计算所需m个样本的协方差矩阵为:

假设A=[x1-ψ,…,xi-ψ,…,xm-ψ],则C=A AT
考虑到使用协方差矩阵求特征值和特征向量所需数据量较大,不利于直接进行人脸特征分类,因此需要对原始人脸图像数据进行降低维度.如何找出最合适且最能代表原始人脸图像的低维度数据则是进行人脸分类的关键所在,所以,在此引入S V D(s i n g u l a r v a l u e d e c o m p o s i t i o n,奇异值分解定理)降低人脸识别维度.
最优投影向量的前i个向量可以用于人脸特征映射,令li(i=1,2,…,p)为矩阵ATA的p个非零特征值,vi为对应于li的特征向量,求得协方差C的正交归一特征向量(i=1,2,…,p),这样就实现将原始k l维的数据降低到p维数据的目的.最后,得到特征脸空间w为:w=(v1,…,vp)
通过上述过程,将每个人脸图像xij对应1个特征向量,利用最小距离分类器对人脸图像进行分类.假设人脸训练样本有C类,第i类有样本图像D个,得到

如果p(Yij,Yx)=m i n(p(Yij,Yx))则训练图像与测试图像同类.
2 IFMPCA算法
2.1 I F M P C A算法思想
虽然传统的P C A算法可以根据S V D进行奇异值分解求得特征脸,然而由于算法所需图像维数较高,整个计算过程仍然需要较长时间.另外,P C A算法受到一定的限制,在某些场合会降低效果甚至失效.场合会降低效果甚至失效.由于算法实现过程中要求人脸训练样本矩阵只有在符合高斯分布的条件下才能使用方差和协方差较好降低数据冗余度.因此,为了在降低计算维数的同时提高人脸识别率,利用子图像之间的差异和关联提高人脸识别效率,采用I F M P C A算法.
I F M P C A算法的基本思想是将一个m×n的标准人脸图像矩阵X分为p×q模块图像矩阵,即

其中,各个子模块分别为人脸样本中具有相似姿态、表情或亮度的图像合集.由于各个子块包含的外在因素较标准训练样本少,所以容易符合高斯分布,能够较好地使用方差和协方差描述噪声和冗余.对每个子模块使用传统P C A算法计算得到满足标准正交的最优投影矩阵Q=[K1,…Li,…,Kr](r 2.2 人脸特征提取 (1)分别对训练样本图像和测试图像分块 人脸训练样本图像Aij的p×q分块矩阵可以表示为: 测试样本图像B的p×q分块矩阵可以表示为: (2)对分块后的子图像进行处理 令(η)kl=V e c(X)kl,其中k=1,2,…,p;l=1,2,…,q,则最优投影向量组Q可提取最大样本特征值所对应的标准正交的向量,表示为: 然而,由于模块P C A方法对人脸数据进行分块处理,引起数据K1,…Ki,…,Kr之间彼此独立,因此,利用模块数据之间的相关性改善特征向量的方法. 首先,求解人脸样本中子模块样本与测试图像子模块之间的距离d((Xtest)kl,(Xij)kl)为: 然后,将样本与测试样本所有子图像的距离进行求和,得到距离D为: 最后,利用这些距离与原有特征向量进行融合,得到新的具有数据相关性的特征向量. 2.3 样本分类 通过分块提取特征,使得每个模块对应一个特征矩阵,利用最小距离分类器进行分类,如果d(Bi,B)=m i n(d(Bi,B)),则样本属于第i类的范畴. 为了证明I F M P C A算法的优越性,实验在Y a l e人脸数据库库上进行.Y a l e人脸数据库是由耶鲁大学计算视觉与控制中心创建,包括15个人的图像,且每个人由11幅姿态、表情、光照变化的图像组成.每幅图像分辨率为100×100.实验选择每个人的前6幅图像作为训练样本,如图1所示,后5幅图像作为测试样本,则训练样本总数为90个,测试样本为75个. 图1 Yale人脸数据库中某一人的6幅图像训练样本 首先,使用传统的PCA算法,计算出人脸识别率.然后,使用IFMPCA算法,对图像进行4×2和4×4分块后分别进行实验得到的结果如图2所示. 图2 IFMPCA和PCA、MPCA人脸正确识别率对比图 从图2中可以看出,对于4×2和4×4两种分块人脸识别情况,IFMPCA方法明显优于传统PCA和MPCA方法. 为了进一步说明IFMPCA算法的性能,将得到最高人脸正确识别率时的最优投影轴的数量、最优特征矩阵维数、特征提取时间及样本识别时间与传统PCA和MPCA算法进行对比,得到实验结果如表1所示. 表1 IFMPCA和PCA、MPCA算法实验结果对比情况 表1中所得到数据表明,在人脸正确识别率方面,对于IFMPCA4×2和4×4两种分块方式以及传统的PCA和MPCA方法进行比较,本文方法的结果明显优于另外两种方法.其中,人脸最高识别率方面,IFMPCA(4×4)的结果是99.1%,PCA的结果是88.9%,MPCA的结果是93.6%,IFMPCA明显优于PCA和MPCA.最优特征维数方面,IFMPCA采用4×2和4×4两种分块方式,最优特征矩阵维数分别为84、200,明显优于PCA和MPCA的最优特征维数.当达到最高识别率时,IFMPCA方法的识别时间分别为0.12和0.17,均大于PCA和MPCA的识别时间分别是0.06和0.11.其原因在于,IFMPCA由于分子模块进行图像识别,花费时间需要计算散布矩阵的特征想念,花费时间较多.PCA由于使用SVD奇异分值理论,节省了大量时间.从总体上讲,IFMPCA方法是PCA和MPCA方法的改进,通过对原始人脸数字图像进行按照光照、姿态等属性进行分块,抽取到每个子图像模块的局部特征,这些局部特征与使用PCA和MPCA方法所提取的人脸图像全局特征相比较更能反映图像各个部分的差异,因此,它的人脸最高识别率优于PCA和MPCA方法,提高了工作效率. 4 结束语 为了弥补传统MPCA忽视训练样本子图像和测试样本子图像之间差异的缺陷,改善人脸识别性能,提出IFMPCA人脸识别算法.IFMPCA方法是一种基于子图像独立特征提取的线性鉴别分析方法,与传统MPCA方法相比,它的突出优点是按照人脸数字图像上相似属性的光照、表情和姿态对人脸标准训练矩阵进行分块,充分考虑训练样本子图像和测试样本子图像之间的差异.实验证明,IFMPCA方法能够有效降低人脸数据维数,减少光照、表情和姿态等因素的影响,较好地提取数据图像的局部特征.但是,如何选择人脸训练样本的最佳分块方式和减少特征提取时间是值得进一步研究的问题. 〔1〕秦宏伟,孙劲光,王强,等.基于自适应预处理和PCA的人脸识别方法的研究 [J].计算机工程与应用,2011,47(14):186-198. 〔2〕Kwak K C,Pedrycz W.Face Recognition Using an Enhanced Independent Component Analysis Approach[J]. IEEE Trans Neural Networks,2007,18(2):530-541. 〔3〕Turk M,Pentland A.Eigenfaces for Recognition[J].Journal of Cognitive Neuroscience,1991,3(1):71-86. 〔4〕Gottumukkal R.Asari V K.An Improved Face Recognition Technique Based on Modular PCA Approach[J]. Pattern Recognition Letter,2004,25:429-436. 〔5〕〔6〕陈伏兵,谢永华.分块PCA鉴别特征抽取能力的分析研究[J].计算机科学,2006,33(3):155-159. 〔7〕Kirby M,Sirovich L.Application of the KL Procedure for theCharacterization of Human Faces[J].IEEE Trans Pattern Analysis and Machine Intelligence,1990,12(1):103-108. TP391.4 A 1673-260X(2012)09-0027-03 2012年度周口师范学院青年科研基金项目(No.J2012QNB03);2012河南省科技攻关项目(No.122400450356)



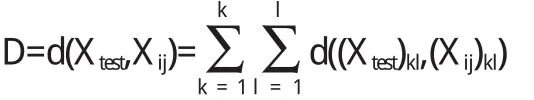
3 实验结果与分析




