光学课程中一个数值仿真例子：光折变离散孤子

陈桂华，谭穗妍，庞 玮

（1.东莞理工学院 电子工程学院，广东 东莞 523808；2.华南农业大学 应用物理系，广东 广州 510642；3.广东工业大学 实验教学部大学物理实验中心，广东 广州 510006）

光学课程中一个数值仿真例子：光折变离散孤子

陈桂华1，谭穗妍2，庞 玮3

（1.东莞理工学院 电子工程学院，广东 东莞 523808；2.华南农业大学 应用物理系，广东 广州 510642；3.广东工业大学 实验教学部大学物理实验中心，广东 广州 510006）

本文用改进的Peaceman-Rachfor（PR）的差分方案对二维非线性薛定谔方程进行研究，通过结合虚时间方法，以缺陷离散系统模型为例子，分别对带缺陷和不带缺陷光折变晶格波导中的离散孤子进行了模拟，所涉及的内容为目前非线性光学及其它非线性物理领域内的前沿问题.此外，这些内容也可以为计算物理课程、量子力学课程以及光学各类数值仿真模块的例子或习题.

二维非线性薛定谔方程；4步Peaceman-Rachfor差分方案；离散系统；离散孤子

1 引言

差分方法作为求解偏微分方程的基本方法有着直观、明、白容易上手的作用.在物理学中，许多的基本方程，如力学中的拉格朗日方程和哈密顿方程，电磁学或光学中的麦克斯韦方程以及量子力学中的薛定谔方程等，其本质都是一系列的偏微分方程.因此，对偏微分方程的构造和求解，成为物理学中间的一个核心内容，同时也是物理学科教学和学习的主要任务.在以往的教学实践中，许多教材以及教师的讲解往往过分注重于数学上解析方法的讲述，使得很多学生在繁重数学公式面前迷失了物理的本质，并由此产生了不知道自己到底在学物理还是在学习数学的困惑.特别现在许多高校在数学、物理等基础课程学时数遭到压缩的时候，不少学生数学和物理素养不够扎实，这一现象就更为凸显.因此，如何结合目前高校物理学课程设置的现状，探索更有效的教学模式，缓解学生在学习过程中产生不必要的困惑以及提高学习效率，成为了物理学教学环节研究中的一个重要问题.

近年来，随着计算机技术和计算机课程的普及，许多基础类或工程类的学科都引入了计算机仿真等模块进行教学，这些模块的引入，使得学生可以更加直观明白有效地理解他们所学习的内容，同时，学生在这些课程和环境的熏陶下，普遍都具有较好的计算机能力.因此，在物理课程中适当引入计算机仿真的模块，对舒缓学生在学习过程中迷失于枯燥的数学公式有一定的作用，而且，引入仿真模块也使得学生更深入地理解数学背后的物理本质有积极的意义.

目前，国内对于物理计算机仿真的课程也逐步增多，例如很多高校都开设了计算物理课程的选修或者必修课程.在这些课程中，我们除了讲解一些基本的算法知识，其核心内容就是介绍各类物理学偏微分方程仿真和求解的数值方法.我们在开展这类课程的时候，需要许多实际的例子或者习题对学生进行讲解和训练.而这些例子或者习题，如果能够和前沿领域挂钩，则既可增加学生的科研能力和学习兴趣，又可以让学生快速地了解和把握物理前沿问题.

本论文这里所讲的4步差分格式Peaceman-Rachfor差分方案，是在简单的Crank-Nicolson差分方案的思路上,基于最简单的差分格式延伸而来的二维差分方案[1].该差分格式通过把二维问题化成一维问题，具有较好的运算效率，而且直观明白，适合课堂中进行讲解及课后进行实践.下面，我们将以离散系统中的非线性薛定方程为例子，讲述这个差分格式与虚时间方法结合在求解二维非线性薛定方程中的仿真运用.

众所周知，光波在线性周期离散系统中传播时会出现一些反常衍射、反常折射及分立衍射等反常现象.这些现象在连续，均匀介质中是从来未有遇见到的[2-3].在传播过程中，当光波与相邻波导之间的线性耦合以及非线性效应平衡的时候，就会形成自局域态.这种自局域态也叫做离散孤子（Discretesoliton）[4-7].在许多科学领域中，离散孤子的研究都是非常热门的研究课题[8].长期以来，人们对离散系统的研究都局限在一维的系统中，近年来通过利用全息技术，在光折变晶体中产生二维的周期的阵列波导并产生离散孤子，使得二维离散系统得以在实验建立[7].由于二维系统要比一维系统展示出更加强大的优越性，使它得到了越来越多科学工作者的关注.特别是近年来，随着全息技术在光子晶体制造方面的技术突破，例如可以通过全息技术制造带缺陷的功能型光子晶体材料[9-10].缺陷的存在对阵列波导中离散孤子的影响和潜在应用也进入了人们的视线[11-12].由于缺陷的种类是多样的，这使得二维非线性薛定谔方程的有效求解也成为了其中一个重要的问题.一般来说，求解二维的薛定谔方程要比一维困难得多，而且耗费机时，占据内存，运算时间长.本文通过对传统的求解二维问题PR差分格式的修改，化成四步，用于求解非线性薛定谔方程，并且应用于模拟二维光折变离散孤子的研究.由于该方法不仅得到比较精确的结果，而且节约计算机时间和无条件稳定，这给人们提供了多一个研究此问题的有效手段，同时，该例子也是目前非线性物理学界的前沿问题，有助于学生通过学习，更多地接触到前沿的物理知识.

24 步PR差分方案的介绍

标准形式的非线性薛定谔方程如下所示：

如图1所示，我们把2维空间（x,y）进行离散化.差分格式从传统P e a c e m a n-R a c h f o r（P R）格式出发，传统的P R差分格式如下：

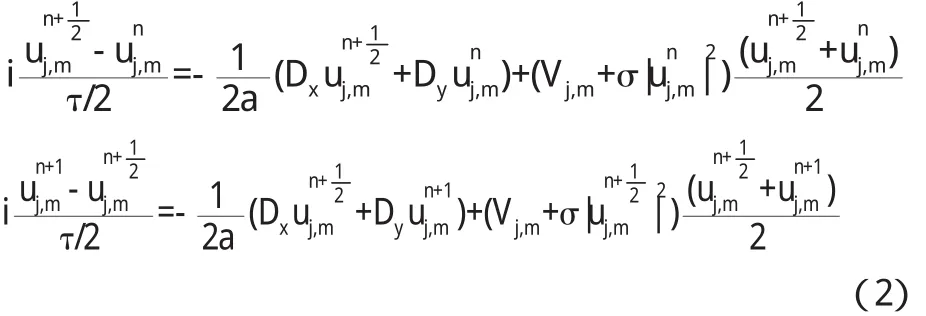
其中：

图1 x，y离散网格

为x，y方向上的二阶分差分格式.

我们把上式化成以下的四步：

以上每一步对于未知的u都是一维求法，其中（3），（5）式为显式，（4），(6)式为隐式.这样的交替差分格式，可以大大的节约了计算时间.同时它和传统的P R格式一样，也是一个具有二阶精度，无条件稳定的差分格式.

假如我们令：方程（1）就会变成标准形式的非线性薛定谔方程，在实际的运行中，我们只需要把步长τ变成τ=-i·c（其中c为一个实数），然后在每一步的演化中都把波函数按照初始功率进行归一化，则是虚时间方法.实践表明，虚时间的收敛性要比松弛法相对较为容易控制.

3 利用4步PR差分方案研究光折变阵列波导中的离散孤子

描述离散孤子在光折变晶体中传播方程的表达形式如下：

在这里，我们已经略去了光折变效应中的光生伏打效应和载流子扩散效应，只保留其中的屏蔽光折变非线性效应.（9）式中的光强I(x,y)=|u|2+|V(x,y)|2，它是用暗辐照Id归一化的光强.V为产生周期阵列波导的光场，一般通过全息技术产生，它的偏振方向和晶体中o光的偏振方向一致（垂直于c轴）.由于光折变晶体一般具有较高的电光各向异性（r13<

在方程里面，ke=k0ne，ne为晶体中e光的折射率.在这里u的偏振方向取作与晶体中e光的偏振方向相一致（平行于c轴）.同时：

图2 无缺陷下离散孤子的光强分布图

（a）用全息技术产生的无缺陷阵列波导的（X Y）示意图

（b）在该阵列波导中离散孤子的（X Y）示意图

（c）离散孤子3维示意图

图3 带缺陷阵列波导下离散孤子的示意图

我们选取具有光折变效应的铁电氧化物S B N作为我们数值模拟的样本，晶体的电光张量系数r33=1340 p m/V，e光折射率ne=2.2229，其横向尺寸取为l=m=5 m m.假设产生周期阵列波导的光场利用全息技术产生，由于目前在全息技术中，可以产生缺陷的全息图像的技术已经出现和被报道，如多光束相位控制技术就是其中一种重要的可以产生缺陷的全息技术[10]，该技术已经被广泛应用于功能性带缺陷的光子晶体的制造中.在这里，我们假设该技术也用于产生带缺陷的周期阵列波导.我们取干涉光强分布为正方格子，其的表达式为：|V(x,y)|2=|V0/2|2K(x,y)[c o s(πx/D)+c o s(πy/D)]2，其中K(x, y)为缺陷函数，在模拟中，我们取|V0|2=4，D=10 μm.加在光折变晶体上的横向电压我们假设为UV=800 V，则横向电场=357 v/m m[7].以下是我们运用该数值方法模拟的一些结果.其中图2描述在无缺陷（K(x,y)=1）的阵列波导及相应的离散孤子的光强分布，而图3则描述阵列波导在负点缺陷情况下（K(x,y)=1-e x p[-(x2+y2)/(0.5 D)2]）的图及其离散孤子的光强分布图.稳定性分析表明，这些孤子解都是稳定的.

以上的模拟是在M a t l a b平台上进行的，现在不少的学科仿真也都基于M a t l a b平台开展[13].同时，M a t l a b软件的编程和应用，是许多高校理工类学生必修、选修或者自学对象.因此，本文的模拟，可以作为计算物理及相关课程的例题或者习题，供学生进行学习和练习.

4 结论

本文利用4步P R算法和虚时间方法相结合，研究了二维阵周期列波导中的离散孤子进行了研究，从模拟的结果来看，算法和传统方法得出的结果相一致，由于4步法把二维化为一维问题去进行计算，所以非常节省计算资源.同时本文所论述的例子，可以作为一些专业课程如计算物理课程、量子力学课程以及光学各类课程数值仿真模块的例子或者习题.通过这一学习和练习，学生既可以掌握利用4步P R算法和虚时间方法相结合的方式处理二维系统的方法，又可以了解到什么是离散系统，什么是离散孤子以及光折边晶体的一些基本知识.对拓展学生的物理知识面有积极的作用.

〔1〕陆金甫，偏微分方程的数值解法(第二版)[M].北京：清华大学出版社，2004.

〔2〕H.S.Eisenberg,and Y.Silberberg, “Diffraction Management,”, Phys.Rev.Lett.85,1863(2000).

〔3〕D.N.Christodoulides,F.Lederer,and,Y.Silberberg,“Discretizing lightbehaviourin linearand nonlinear waveguide lattices”,Nature,424,817(2003).

〔4〕F.Lederer,C.I.Stegeman,et.al. “Discrete solitons in optics”,Physics Reports,463,1-126(2008).

〔5〕H.S.Eisenberg,and Y.Silberberg, “Discrete Spatial Optical Solitons in Waveguide Array”,Phys.Rev.Lett. 81,3383(1998).

〔6〕N.K.Efremidis,S.Sears,et.al. “Discrete solitons in photorefractive optically induced photonic lattices”,Phys. Rev.E.66,046602(2002).

〔7〕J.W.Fleischer,M.Segev,et.al. “Discrete solitons in optically induced nonlinear photonic lattices”,Nature, 422,147(2003).

〔8〕S.Flach,A.V.Gorbach, “Discrete breather-Advances in theory and applications”,Physics Reports,467,1-116(2008).

〔9〕X.S.Xie,M.Li,et.al. “Phase manipulated multibeam holographic lithography for tunable optical lattices”,Optics Express,15,7032(2007).

〔10〕Juntao Li,Yikun Liu,et.al. “Fabrication of photonic crystals with functional defects by one-step holographic lithography”,Optics Express,16,12899(2008).

〔11〕I.Makasyuk,and Zhigang Chen, “Band-Gap Guidance in Optically Induced Photonic Lattices with a Negative Defect”,Phys.Rev.Lett.96,223903(2006).

〔12〕B.Freedman,G.Bartal,et..al.“Wave and defect dynamicsin nonlinearphotonic quasicrystals”,Nature, 440,1166(2006).

〔13〕黎永耀,麦志杰,吴剑雄,付神贺,刘岩.基于Matlab平台下量子力学课中的“实验”课[J].赤峰学院学报,2011,27 (10):13-14.

O43

A

1673-260X（2012）09-0010-03

国家自然科学基金项目（10947140，11104083）