偏微分方程数值解法的研究

王海林，徐 珊，宋论兵，高全归

（玉溪师范学院 物理系，云南 玉溪 653100）

偏微分方程数值解法的研究

王海林，徐 珊，宋论兵，高全归

（玉溪师范学院 物理系，云南 玉溪 653100）

本文将从两个方面来讨论偏微分方程的数值解法，其一为网格比对数值解法的影响，其二为不同差分格式对偏微分方程数值解法的影响，这两个方面都会影响偏微分方程数值解的结果.

偏微分方程；数值解；稳定性

随着科学技术和社会的发展，大量复杂的计算问题不断出现在人们面前.在计算机没有问世之前，为了解决某些复杂的计算问题，不少科学家献出了大半生，甚至毕生的精力，1867年法国天文学家达拉姆尼（D a l a m n y）花了整整20年的时间，求解了一个天体运动的摄动级数展开式[1].但这并不是解决复杂问题的好方法，于是人们开始研究解决复杂计算问题的方法，为了解决一些复杂的计算问题，数值计算方法便出现了.而偏微分方程的数值解是其中一个非常重要的分支，例如要准确预测天气的变化情况，就要求解成千上万个偏微分方程组[1]，人工求解是很不现实的，因而，偏微分方程的数值解就显得相当重要了.偏微分方程的数值解法主要有三种，有限差分法，变分法，有限元方法，使用最普遍的是有限差分法.而有限差分法在求解偏微分方程的时候会存在不稳定性，所以，需要分析有限差分法求解偏微分方程的稳定性，差分方程的稳定性是指研究差分方程在右端自由项无误差的情况下，初值干扰对差分方程解的影响，它反映了差分解是否连续依赖于初值的情形[2]，有限差分法又存在很多种差分格式.本文将从两个方面讨论偏微分方程的数值解法.本文的第一部分将对有限差分法做个简单介绍，第二部分将给出网格比对稳定性的影响，第三部分将给出具体的差分格式对数值解的影响，第四部分内容为本文的结论与讨论.

1 有限差分法简介

考虑偏微分方程中最简单的一维对流方程的初边值问题：

要利用数值方法求解上述定解问题，首先需要对定解区域离散化，用平行直线族xj=j h，tk=k τ，把区域D划分成若干个小矩形，其中h，τ称为空间步长和时间步长，τ称为网h格比（如果为二阶的网格比可表为等）.接下来对微分方程离散化，由泰勒级数展开可知，在接点(j,k)处微商和差商存在如下关系[3]：

最后将边界条件和初始条件离散化后就可以做数值计算了.

2 网格比对偏微分方程数值解的稳定性影响

为了计算方便，取方程（1）中的a=1，这样方程（1）对应的差分方程可以写为：

图1 其中实线代表网格比为=1.1，虚线代表网格比为=0.9，点线代表网格比为=1.0

由上面的计算可知网格比会影响方程数值解的稳定性.这里只是直观的给出方程数值解的稳定性的状况.数值解的稳定性的分析可以采用F o u r i e r方法，H i r t启示性方法，能量不等式方法等[3].

3 不同差分格式下的偏微分方程数值解

对于不同的差分格式下的偏微分方程的数值解依然采用方程（1），分别采用下面的四种差分格式做差分：

（1）迎风格式的差分方程可以写为：

（2）L-F（L a x-F r i e d r i c h s）格式的差分方程可以写为：

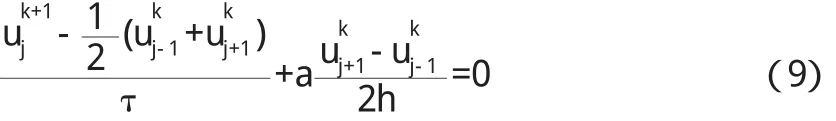
（3）L-W(L a x-We n d r o f f)格式的差分方程可以写为：

（4）B e a m-Wa r m i n g格式的差分方程可以写为[4]：

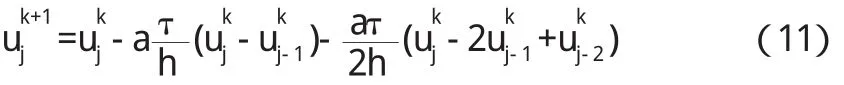
图2 迎风格式

图2、图3、图4、图5分别为上述四种差分格式对应的数值解的函数图象.计算过程中取h=0.01，网格比取=0.5，上图为对时间计算100步后所得到的函数图象，由图可知，图4，图5出现了震荡，图2，图3比较平滑，这是由于差分格式不同所导致的.

图3 L-F格式

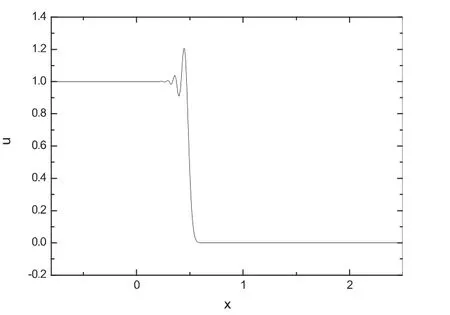
图4 L-W格式

图5 B e a m-Wa r m i n g格式

4 结论与讨论

从上面的计算可知，运用有限差分法求解偏微分方程，网格比会对方程的解的稳定性存在影响.而不同的差分格式会使得方程的解存在微小差异，并且其稳定状况也不一样，因而，在解决实际问题的过程中，求解偏微分方程的需要注意选择合适的网格比及适当的差分方法，这样对于偏微分方程的求解是有帮助的.

〔1〕周煦.计算机数值计算方法及程序设计[M].北京:机械工业出版社,2004.

〔2〕徐长发,李红.偏微分方程数值解法[M].武汉:华中科技大学出版社,2000.

〔3〕陆金甫,关治.偏微分方程数值解法[M].北京:清华大学出版社,2004.

〔4〕LeVequeR J.NumericalMethodsforConservation Laws.Basel:Birkhauser Verlag,1990.

O 175.2

A

1673-260 X（2012）09-0001-02

玉溪师范学院大学生创新性实验计划项目（2011B17）