集值映射空间与超空间的继承稠密度和继承Lindelöf度

杨春梅，李祖泉

（杭州师范大学理学院，浙江杭州310036）

集值映射空间与超空间的继承稠密度和继承Lindelöf度

杨春梅，李祖泉

（杭州师范大学理学院，浙江杭州310036）

利用连续集值赋值映射和弱拓扑讨论了集值映射空间的继承稠密度和继承Lindelöf度，获得了点态收敛拓扑空间（X）上hd（（X））和hl（（X））与基本空间X的对偶性以及紧开拓扑空间（X）上hd（X））和hl（X））与基本空间X的对偶性，推广了单值连续集值映射空间（X）的相关结论.

集值映射空间；超空间；继承稠密度；继承Lindelöf度；弱拓扑

0 引 言

Zenor P［1］和McCoy R A［2-3］对函数空间（X）在赋予紧开拓扑下的继承稠密度和继承Lindelöf度进行了系统研究，腾辉，林寿［4］对点态收敛函数空间Cp（X）给出了继承稠密度和继承Lindelöf度的等价刻画，并且指出了McCoy R A的证明中的错误.本文研究了点紧连续集值映射空间（X）和（X）与基本空间X和的继承稠密度和继承Lindelöf度的对偶不等式定理，给出了（X）上hd（（X））和hl（X））以及（X）上hd（k（X））和hl（X））的两个对偶性证明.

本文中，拓扑空间X是Hausdorff空间，K（X）表示X的所有非空紧子集族，ω表示可数序数，ℕ表示自然数集，ℝ表示实直线，（X）为X到ℝ上的所有点紧致的连续映射族，p（X）为（X）赋予点态收敛拓扑，k（X）为（X）赋予紧开拓扑.文中未定义的术语和符号均以［3］，［5］和［6］为准.

1 预备知识

对于X的子集K，ℝ的子集U，V，记W＋［K；U］＝｛f∈k（X）：f（K）⊂U｝；W-［K；V］＝｛f∈k（X）：f（x）∩V≠φ，x∈K｝.

定义1 以所有形如W＋［x；U］，W-［x；V］的集为子基作为（X）的拓扑，其中x∈X，U，V为ℝ的开子集.该拓扑称为点态收敛拓扑，记为p（X）.

定义2 以所有形如W＋［K；U］，W-［K；V］的集为子基作为（X）的拓扑，其中K∈K（X），U，V为

的集生成，其中K∈K（X），k∈ℕ，V1，V2，…，Vk为ℝ中的开集.证明 由定义，k（X）的基开集由形如W＋［K，U］，W-［K，V］的集的有限交

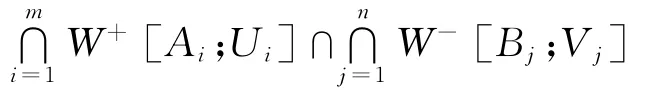
生成，其中Ai，Bj∈K（X），开集Ui，Vj⊂ℝ，1≤i≤m，1≤j≤n，m，n∈ℕ.容易证明∩mi＝1W＋［Ai；Ui］∩∩nj＝1W-［Bj；Vj］＝∩mi＝1W［Ai；Ui］∩∩nj＝1W［Bj；Vj，X］.另一方面，对于任意K∈K（X），开集Vi⊂ℝ，1≤i≤k，k∈ℕ，W［K；V1，V2，…，Vk］＝∩ki＝1W-［K；Vi］∩W＋［K；∪ki＝1Vi］.

2 主要结果

设X是拓扑空间，X的继承稠密度hd（X）定义为：（hd）（X）＝ω＋sup｛d（A）：A⊂X｝.特别地，若hd（X）＝ω，则称X是继承可分空间.X的继承Lindelöf度hl（X）定义为：hl（X）＝ω＋sup｛L（A）：A⊂X｝.特别地，若hl（X）＝ω，则称X是继承Lindelöf空间，其中d（A）和L（A）分别代表子集A⊂X的稠密度和Lindelöf度.

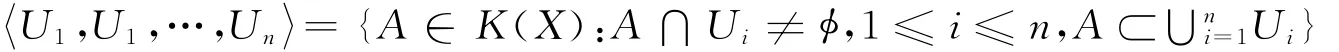
空间X上的紧子集超空间K（X）的基为形如形式，其中n∈ℕ，Ui（1≤i≤k）是X中的开集.由［7］命题4.5.1，有w（K（X））＝w（X）.

定义4 设X，Y和Z是拓扑空间，f：X×Y→Z是点紧致的集值映射.对于y∈Y，定义集值映射fy：X→Z为fy（x）＝f（x，y）；类似地，对于x∈X，定义集值映射fx：Y→Z为fx（y）＝f（x，y）.若对于每一个y∈Y，fy是连续的，则称f是在X上的连续的；同理，若对于每一个x∈X，fx是连续的，则称f是在Y上连续的.

定理1 设X，Y和Z是拓扑空间，f：X×Y→Z是点紧致的集值映射.f是在Y上连续的，且X具有使得f是在X上连续的弱拓扑，则下列结论成立：（a）hd（X）≤hl（Y）·w（K（Z））；（b）hl（X）≤hd（Y）· w（K（Z））.

（a）设A⊂X，因为f是在Y上连续的，对于n∈ℕ，Ui∈，1≤i≤n，令

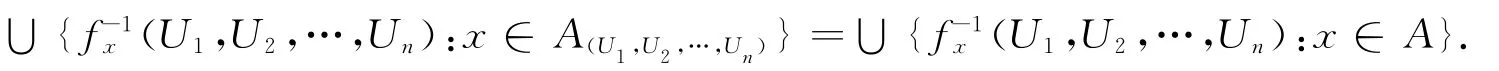
令A′＝∪｛A（U1，U2，…，Un）：（U1，U2，…，Un）∈＃｝，则｜A′｜≤hl（Y）·w（K（Z））.下面证明＝A.设x∈A，V为含x的开邻域，因为X具有使得f是在X上连续的弱拓扑，则是X的基.从而存在y∈Y，（U1，U2，…，Un）∈＃，使得.而U2，…，Un），所以存在使得.从而，即x′

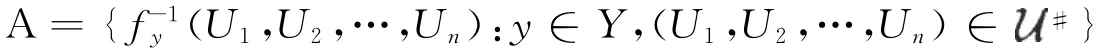
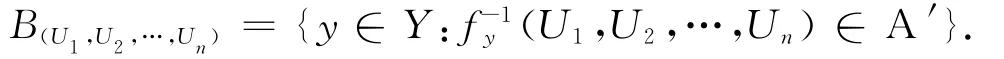
则对于B（U1，U2，…，Un）的每个稠密子集B′（U1，U2，…，Un），有｜B′（U1，U2，…，Un）｜≤hd（Y）.令

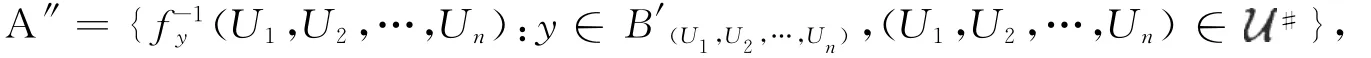
则｜A″｜≤hd（Y）·w（Z）.下面证明：∪A′＝∪A″.显然有∪A″⊂∪A′.设x∈∪A′，那么存在（U1，使得.从而U2，…，Un），所以存在.因此，故x∈∪A″.

推论1 设f：X×Y→ℝ是点紧致的集值映射.X，Y上的拓扑是使得f在X和Y上均是连续的弱拓扑，则hd（X）＝hl（Y）且hl（X）＝hd（Y）.

证明 因为w（ℝ）＝ω，由w（K（ℝ））＝w（ℝ）＝ω，则hd（X）≤hl（Y）·w（K（ℝ））＝hl（Y）且hl（X）≤hd（Y）·w（K（ℝ））＝hd（Y）.由X和Y的对称性，有hd（Y）≤hl（X）且hl（Y）≤hd（X）.从而hd（X）＝hl（Y）且hl（X）＝hd（Y）.

定理2 对于拓扑空间X，下列结论成立：（a）hd（X）≤hl（p（X））；（b）hl（X）≤hd（p（X））.

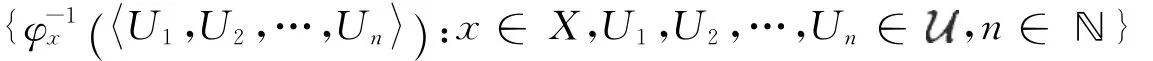
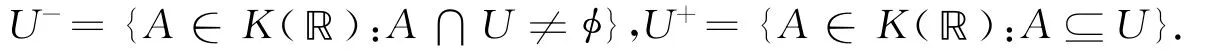
则形如U-，U＋的集是K（ℝ）的子基开集.由

可知φf为X上的连续集值映射.从而由定理1知hd（X）≤hl（p（X））·w（K（ℝ））＝hl（p（X））及hl（X）≤hd（p（X））·w（K（ℝ））＝hd（p（X））.

定理3 对于拓扑空间X，下列结论成立：（a）hd（X）≤hl（k（X））；（b）hl（X）≤hd（k（X））.

设f∈W＋［K；U］，则f（K）⊂U.对于x∈K时，有f（x）⊂U.因为f是连续映射，则f（x）为紧集，从而存在包含f（x）的开集W，使得f（x）⊂W⊂W⊂U.所以存在K的开子集Vx，使得x′∈Vx，且有是闭集，有，即.对于任意.因为K是紧的，存在x1，x2，…，xn∈K，n∈ℕ，使得

设f∈W-［K；U］，对于x∈K，有f（x）∩U≠φ.设y∈f（x）∩U，则存在包含y的ℝ中的开集W，使得.因为f是连续映射，所以存在K的开子集Vx，使得当x′∈Vx时，f（x′）∩W≠φ，即Vx⊂f-（W），从而由）为闭集，有.对于任意，有φ（x′，f′）⊂U.因为K是紧的，存在x1，x2，…，xn∈K，n∈ℕ，使得.从而W-.

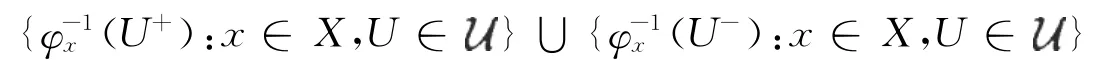
推论3 对于拓扑空间X，有：

［1］Zenor P.Hereditary m-seperability and the hereditary m-lindelöf property in product spaces and functions［J］.Fund Math，1980，106：175-180.

［2］McCoy R A.Countability properties of function spaces［J］.Roc Moun Jour Math，1980，10（4）：717-730.

［3］McCoy R A，Ntantu I.Topological Properties of Spaces of Continuous Functions［C］／／Lecture Notes in Math，Berlin：Springer-Verlag，1988：1315.

［4］腾辉，林寿.函数空间的遗传稠密度和遗传Lindelöf度［J］.科学通报.1993，38（1）：1-4.

［5］林寿.度量空间与函数空间的拓扑［M］.北京：科学出版社，2004.

［6］Engelking.General Topology［M］.Warszwa：Polish Scientific Publishers，1977.

［7］Michael E.Topologies on spaces of subsets［J］.Trans Math Soc，1951，71：152-182.

On Hereditary Density and Hereditary Lindelöf Degree of Multifunction Spaces and Hyperspaces

YANG Chun-mei，LI Zu-quan

（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

This paper discused the hereditary density and the hereditary Lindelöf degree of multifunction spaces by means of evaluation multifunction and weat topology，obtained two dualities of point-wise convergent topological spacek（p）with basic Xand compact-open topological spacek（X）with basic Xabout hd（p（X）），hl（p（X））and hd（k（X）），hl（k（X））.These results extended related conclusions of function spaceκ（X）.

multifunction space；hyperspace；hereditary density；hereditary Lindelöf degree；weak topology.

11.3969／j.issn.1674-232X.2012.02.018

O189.1 MSC2010：54A25

A

1674-232X（2012）02-0185-04

2011-09-17

李祖泉（1963—），男，教授，主要从事一般拓扑学研究.E-mail：hzsdlzq＠sina.com