直升机起落架机轮轴载荷分析与强度校核

李 兵，魏 敏，刘振江，朱英杰，张东波

（1.石河子大学机械电气工程学院，新疆 石河子 832003；2.69008 部队，新疆 五家渠 831300）

直升机作为能垂直起降的飞行器，对着陆起降场地要求不高，被人们广泛应用在各种场合，起落架在其日常使用中发挥了重要的作用，因其起降频繁，起落架与地面的常态化刚性碰撞，起落架的关键部位较容易损坏，给直升机的安全使用带来隐患。而机轮轴是连接机轮系统与摇臂及缓冲减震装置的纽带，是起落架的关键零件，在起落架的着陆和地面滑行中要承受很大的交变冲击载荷[1]，对起落架设计方案的决策起着重要的参考作用，机轮轴对保证起落架功能的正常使用发挥着举足轻重的作用。鉴于此，对机轮轴展开载荷分析，进行强度校核以及有限元仿真有非常重要的实践指导意义。

1 设计要求及其着陆过程受力分析

起落架要求是直升机以一定速度着陆时，起落架的结构强度达标，且直升机的垂直过载Ω 小于2[2]。起落架外观如图1 所示。

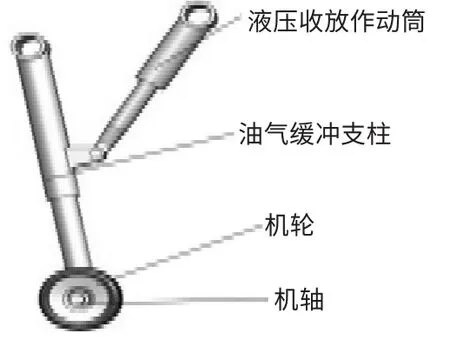
图1 起落架系统结构示意简图

起落架载荷分析过程如下：假定起落架触地瞬时直升机动能为W，重力势能为H，直升机着陆速度为ν，当速度由ν 降为零时，起落架的应力应变在这个瞬间达到最大。直升机向下位移的距离为h，此时直升机的动能W 和重力势能H 变为零。

其重力势能的变化量为：

动能变化量为：

其中，

m 为直升机机体品质，等于3 500 kg；ν 为触地前速度，轮式直升机着陆速度一般小于10 m/s，取ν=12 m/s。

在直升机降落的过程中，其旋翼升力做功减少了由重力势能所带来的能量转化，同时这个过程中升力小于直升机重力，取升力为

则升力做功

设直升机下降速度变为0 时，地面的反作用力为F，其变形程度在线弹性范围内，同时材料受力与变形成正比关系，变形所吸收的能量等于地面反作用力所做的功。

由以上各式可得：

式中F 和h 为未知参数，因为变形在线弹性范围，F 与起落架的变形成正比，可设

根据材料力学中单位载荷方法[3]，在对称结构的一端施加1 N 竖直方向上的单位载荷进行分析即可，根据此方法算出起落架机轮轴的变形，就可以得出线性系数的λ 的数值，再把上式代入（6）式中就可以得到一个以h 为未知量的一元二次方程，可以求出h，进一步可得到地面最大反作用力F 和垂直过载Ω。

2 载荷计算

起落架机轮轴采用直径为50 mm 的30CrMnSiE材料，其受力简图如图2 所示。

图2 起落架受力简图及坐标系参数

地面反作用力引起的力矩为

单位力1N 所引起的力矩为

机轮轴截面的惯性矩

机轮轴在数值方向上的变形为

把（7-11）各式代入上式中，计算可知

δ=0.017 326 f=1.732 6×10-2F，单位：mm

当单位作用力F 为1N 时，变形δ =1.732 6 ×10-5m

因此，线性系数为

进而，F=λh=5.771 7×104h

将F=λh 代入机械能守恒方程

可得关于h 的一元二次方程式

解得，h=1.111 3 m

则地面最大反作用力为

所以垂直过载为

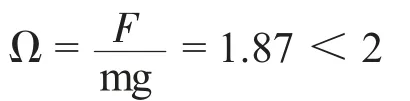
根据计算可得出垂直过载小于2，满足过载要求。

3 应力分析及强度校核

只要考察最大载荷下的应力与强度，即为前飞降落时[4]，只要屈服力小于最大许用力则可。

取竖直方向载荷F1=2/5 F，水平方向载荷F2=1/2 F1，则

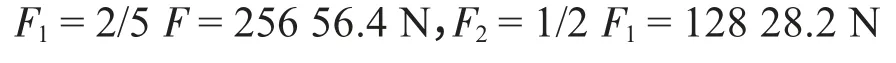
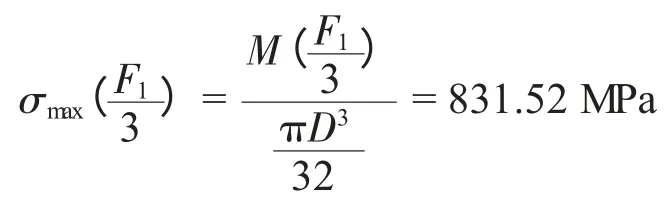
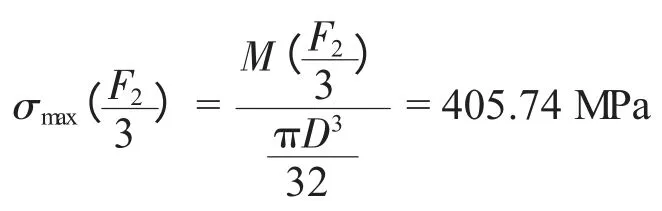
机轮轴中央截面处附近的正应力为

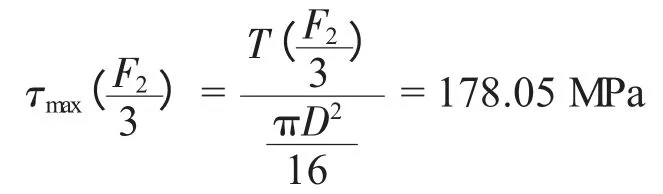
机轮轴中央截面中最大应力单元体的应力状态如图3 所示。

图3 最大应力处单元的应力状态

由最大主应力计算公式计算，可知

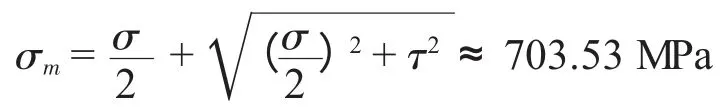
材料30CrMnSiA 的屈服极限为885 MPa[5]，取安全系数为1.2，则许用应力为

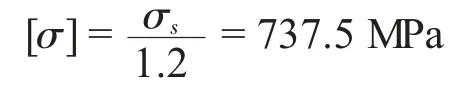
可知，最大正应力σm＜[σ]，故满足强度要求。

4 结束语

通过对起落架机轮轴的过载分析，并进行了强度校核，从力学角度完整的研究了机轮轴工作情况。机轮轴的材料具有其特点，有着特定的要求，一方面,其需要有足够的强度，须承受得住足够大的应力施加；另一方面，其要求具有一定程度的弹塑性，能根据受力情况的不同产生变形提供缓冲能力，以达到减弱地面反作用力与垂直过载，故在其设计中，要考虑到这些潜在要求。

在计算中发现，机轮轴中间部分承受应力较大，可以考虑适当增大此部分的横截面面积。这样的设计，首先最大限度地利用了材料，达到减轻质量的目的；其次制造工艺难度增加，导致生产成本增加。鉴于此应整体考虑，统筹兼顾的决策起落架机轮轴的设计方案。

[1]罗漳平，向锦武. 直升机起落架抗坠毁性能的有限元仿真评估[J].航空学报，2003，24：216-219.

[2]王 昂，毛德华，等.飞机设计手册[M].北京：航空工业出版社，2005.

[3]单辉祖.材料力学[M].北京：高等教育出版社，2004.

[4]杨嘉陵,吴卫华. 武装直升机抗坠毁设计研究[J]. 机械工程学报，2001，37：78-82.

[5]闻邦椿. 机械设计手册（第5 版）[M]. 北京：机械工业出版社.2010.