低速重载行星齿轮传动啮合特性分析
柳忠良,陈 刚,钟 明,李 虎
(上海振华重工(集团)股份有限公司,上海 200125)
与普通齿轮传动相比,行星齿轮传动具有质量小、体积小、传动比大及效率高等优点。因此,行星齿轮传动,已广泛应用于工程矿山机械、冶金机械、起重运输机械、海洋工程机械等各个领域[1~3]。行星传动不仅适用于高转速、大功率传动,而且也被应用在低速重载的传动装置上。目前,行星传动技术已成为世界各国机械传动设计研发的重点之一[4]。
随着行星传动技术的迅速发展,行星齿轮传动装置所传递的载荷也在不断增大。据相关资料介绍,目前传递功率已达到2 000 kW,输出转矩已超过4 500 k N·m。低速重载行星齿轮传动装置,是目前齿轮传动技术的重点发展方向之一[5]。
1 行星传动基本组成概述
行星传动结构主要由图1中的太阳轮、行星轮、轴承、齿圈、行星轮轴、行星架等6个部件组成。其中太阳轮和齿圈又可称做中心轮,在载荷传递中,太阳轮、齿圈及行星架这3个部件,可互为输入输出。

图1 行星传动基本组成图
在行星传动中,沿齿宽方向的载荷,称为齿向载荷分布;沿齿轮半径方向的载荷,称为径向载荷。
2 行星传动齿轮啮合特性
2.1 齿轮齿向载荷分布特性
依据材料本身特性,材料所承受的载荷小于屈服应力值时,会出现弹性变形,而且载荷越大,变形越大,行星传动机构,通常采用的结构布置如图1所示。
机构在承受载荷后,由于材料弹性变形,行星架会出现扭转变形(如图2所示),行星轮轴会出现弯曲变形(如图3所示),使得传动机构在运行过程中,任意行星轮的回转轴线和中心轮的回转轴线出现偏差Lxi,Lxi可近似用图4表示。
并可用下述公式表达

其中,
Fi'为任意行星轮承受的外部载荷;
ki'为经过任意行星轮的输入及输出路径上的综合弹性系数(ki'不包含该行星轮和中心轮的啮合弹性系数)。

图2 行星架扭转变形示意图

图3 行星轮轴弯曲变形示意图
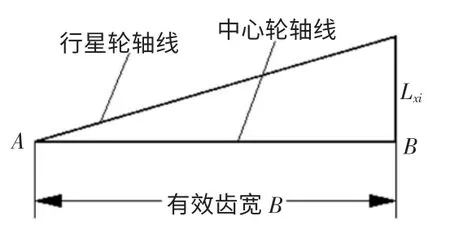
图4 行星轮和中心轮轴线偏差示意图
由于行星轮轴线和中心轮轴线不平行,在载荷的作用下,行星轮与太阳轮啮合时,齿部首先会在图4所示的A 点接触。随着载荷力的增大,齿面弹性变形增大,最终B 点也接触。如继续加载,此时增加的载荷,会均匀分布在有效齿宽B 上。
因此,在此条件下的行星传动中,A 点的受力Fxmax最大。假设行星轮个数为n,太阳轮直径为d,太阳轮传递的扭矩为T,任意行星轮和中心轮齿部啮合弹性系数为kxi,则Fxmax可用下述公式表示

对行星机构而言,ki'、kxi、n、d 均为固定值,不随载荷的变化而变化;而从式(1)可以看出,外部载荷Fi'加大,会导致Lxi变大;从式(2)可知,Lxi加大,会直接导致啮合面最大受力Fxmax的加大,最终使齿向载荷的分布更不均匀。
2.2 齿间载荷分布特性
行星传动中的行星轮个数,通常大于等于3个,对于3个行星轮的传动装置,只要采用浮动构件,就可很好地实现行星轮与中心轮之间的均载,但总的承载能力不强。低转速大扭矩传动的行星机构,通常采用大于或等于4个行星轮(后续称之为多行星轮)的传动形式。由于制造、装配存在误差,多行星轮传动机构的行星轮轴线,不可避免地会不在同一个理论圆周上。
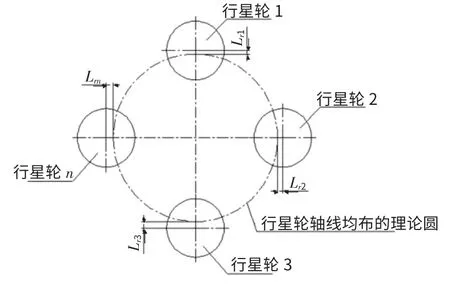
图5 行星传动载荷分布不均示意图
如图5所示,Lrn为行星轮轴线偏离理论圆的距离,假设Lr1≤Lr2≤Lr3……≤Lrn,行星传动机构在运行时,当行星架转动Lr1时,首先行星轮1进行齿部啮合受载,当行星架转动Lr2时,行星轮1、2进行齿部啮合受载,以此类推。当行星架转动Lrn时,行星轮1、2、3……n 均进行齿部啮合受载。当行星架再次同方向转动时,增加的传递载荷,则均匀地分布在各个行星轮上。此时,最先接触的行星轮1齿部承受的载荷Fxmax最大;设定通过每个行星轮的载荷传输路径上的总的弹性系数相等且均为kr,则Fxmax可用下述公式表示
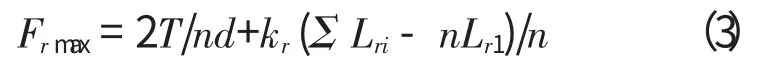
从式(3)中可以看出,对一个既定的行星传动机构而言,最大的齿间载荷,取决于弹性系数kr和行星轮轴线偏离理论圆的距离Lrn之间的一致性,而Lrn的一致性则由齿轮、行星架、行星轮支撑轴承的加工、装配精度决定。
对于太阳轮和行星架浮动的行星结构,如行星轮数小于等于3,可以实现
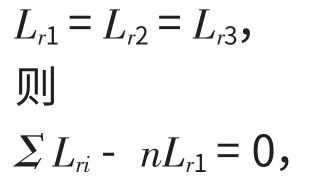
因此,行星轮的最大载荷Fxmax=0,齿间载荷分配能实现有效的平均分布;
对于行星轮数大于等于4的行星机构,通过浮动组件,最大能实现3个行星轮轴线偏离理论圆的距离Lr1~Lr3之间的一致性,其他行星轮轴线必然在理论圆以外,而且与Lr1~Lr3的偏差越大,则行星轮最大载荷Fxmax越大。
对于无浮动组件的行星传动结构,Lri之间的一致性较差,则Σ Lri-nLr1=0,的值较大,此时,在同等加工精度条件下,行星轮最大载荷Fxmax最大。
3 举例说明
以表1的参数,结合图1为例,通过输入同样的载荷,分别对下列3种情况下的齿部受力,进行有限元计算,并比较行星轮啮合齿部的受力情况,对齿向载荷分布不均和齿间载荷分布不均的影响做进一步说明。

表1 行星传动机构参数
情况A:行星轮的回转轴线都在理论圆周上,和中心轮的回转轴线完全平行(理想状态);
情况B:行星轮回转轴线和中心轮回转轴线在有效齿宽内有0.08mm的偏差;
情况C:3个行星轮的回转中心在同一个理论圆周上,一个行星轮的回转中心在理论圆周往内偏0.08mm的位置上;
从图6和图7中齿部最大应力值可以看出,行星轮回转轴线和中心轮回转轴线无偏差时,最大齿部应力为116.528MPa,两轴线在有效齿宽内有0.08mm的偏差时,齿部最大应力值是153.256MPa,约是无偏差时的132%。

图6 情况A 时行星轮齿部应力

图7 情况B 时行星轮齿部应力
从图8中齿部最大应力值可以看出,一个行星轮的回转中心在理论圆周往内偏0.08mm时,齿部最大应力是128.996MPa,约是无偏差时的111%。

图8 情况C 时行星轮齿部应力
综合分析上述A、B、C 共3种情况下的有限元计算结果,可以看出,无论是行星传动的齿向载荷不均,或齿间载荷不均,都会造成齿部啮合处的应力增大,并且齿向载荷的影响更大。
4 解决措施
对于行星传动齿轮齿向载荷分布,由式(1)、式(2)可知,增大任意行星轮的输入及输出路径上的综合弹性系数ki'或减小任意行星轮和中心轮齿部啮合弹性系数为kxi,可减小齿部最大受力Fxmax,但无法完全消除行星架和行星轮轴变形带来的影响。
采用图9的结构,可以完全消除行星架和行星轮轴变形带来的影响。

图9 行星传动载荷分布改进结构示意图
图9中的自调心轴承3工作时,允许内外圈有一定的相对转角,当行星架和行星轮轴受载后,其产生的变形,被自调心轴承的内外圈相对转动所抵消,从而保证行星轮和中心轮的轴线平行,啮合部位齿向载荷分布均匀。
对于大于或等于4个行星轮的行星传动齿间载荷分布,由式(3)可知,最大的齿间载荷Fxmax取决于弹性系数kr和行星轮轴线偏离理论圆的距离Lrn之间的一致性;加工精度越高,Lrn的一致性就越好,则最大的齿间载荷Fxmax越小,但相应的成本越高;也可采用减小弹性系数kr的方法,减小最大的齿间载荷,例如图9所示。在满足强度要求的前提下,尽量减小行星轮轴径,并在行星轮中心打圆孔,同时将轴承放置于中间部位,均可减小弹性系数kr,从而减小最大的齿间载荷。
5 结束语
行星传动结构中,齿轮齿向载荷分布不均现象,会随着输入载荷的增加而加剧。通过有限元分析可知,齿向载荷分布不均,带来的附加应力占的比例较高,这对低速重载行星传动极为不利,采用行星轮单调心轴承支撑的机构方式,可完全消除齿向载荷分布不均。
多行星轮传动中的齿间载荷分布不均现象,目前没有办法完全消除,但可通过改变加工装配精度和行星轮载荷传输路径上总的弹性系数kr来减小最大齿间载荷。加工、装配精度越高,行星轮分布的一致性越趋于良好,从而实现齿间载荷分布均匀;弹性系数kr越小,同样行程内产生的附加载荷就越小,则齿间载荷分布越好。
针对行星传动机构分析过程中存在的问题,通过采取有效措施,达到消除或减小载荷分布不均的目的,同时,可使低速重载减速箱趋于小型化,轻量化,节约成本,提高市场竞争力。
[1]卢济武.低速大转矩行星减速箱设计研究[M].上海:煤炭科学研究总院上海分院,2005.
[2]成大先.机械设计手册[M].北京:化学工业出版社,2002.
[3]Ligata H,Kahraman A and Singh A.A Closed-Form Planet Load Sharing Formulation for Planetary Gear Setsusing a Translational Analogy[J].JournalofMechanicalDesign,2009,(131):1-7.
[4]Ligata H,Kahraman A and Singh A.Internal Gear Strains and Load Sharing in Planetary Transmissions:Model and Experiments[J].Journal of Mechanical Design,2008,(130):1-10.
[5]Singh,Avinash.Application of a System Level Model to Study the Planetary Load Sharing Behavior[J].Journal of Mechanical Design,2005,(127):469-474.

