基于遗传算法的多资源平衡工序排序优化决策
付宗仁
(海军91832部队装备部,广西 北海 536000)
生产过程中工序编排是生产管理中极其重要的一个环节,处理得好与坏,直接影响产品的生产周期及经济效益,对此人们已有充分的认识。但工序排序属N-P完备问题,至今尚无特别简便、有效的方法加以解决,人们一般沿袭传统作法凭经验办事,或用一粗糙的近似算法,效果都不理想。随着计算机在生产过程中的广泛应用,使用它们解决排序问题,已成为一种快捷、有效的途径。
工序编排有两类问题,一是基于资源约束,通过合理安排工序寻求最短的生产周期,从而尽快完成任务;一是在总工期不变即固定工期的情况下,通过工序编排,使各资源需求数量尽可能达到平衡使用,以减少资源储备或使工程物资供应有保障,从而增强实现计划的可能性,并通过资源平衡,达到减少资源闲置与浪费、降低工程成本的目的。
目前,人们对上述第一类问题研究的较多、较为深入,对于多资源平衡优化的问题研究并不多。文献[1]通过确定各资源对平衡效果的相对贡献率,分析了时差对工序调整的影响,构造了综合判断数量指标,比较符合工程施工对资源量的需求情况,但并没有应用有效的算法进行计算,难以高效的实现。文献[2]应用改进的混合遗传算法求解了第一类问题。文献[3]对活动网络资源均衡问题的建模和算法分别进行了讨论,提出了资源均衡的遗传算法。文献[4]使用聚类分析优化遗传算法对资源平衡进行了研究。同时较多文献只是对简单的总工期固定多资源进行描述和建模,而且对于目标值及适应度函数的表达不直接,显得较为烦琐。
本文建立了典型的网络计划多资源平衡工序优化的数学模型,应用MATLAB遗传算法工具箱函数及改进的遗传算法对其进行了研究,设计了可直接求解出最佳工序编排及其对应的目标函数值的功能函数,使建模过程及结果简洁明了,并获得了满意的计算效果。
1 多资源平衡工序排序优化决策
1.1 多资源工序平衡优化设计数学模型
对于多资源工序平衡问题,前提假设是总工期为固定工期,设为T,即在时间T内完成任务。由于是寻求资源平衡利用,故不需提前完成。
针对一般的问题,设有n 道工序P1、P2、…Pn,各工序之间的逻辑关系、持续时间LT(Pi)、每道工序所需资源量Zj(Pi)为已知。那么根据各工序之间的逻辑关系和持续时间就可制订出网络计划图,计算出各工序最早/最晚开工时间、最早/最晚完工时间(其分别记为ES(Pi)、LS(Pi)、EF(Pi)、LF(Pi)),并得出可进行调整的工序名称及其可调整量,进而得出设计变量的维数及变量范围。多资源平衡工序的优化目标是:
(1)总工期中的单位时间内某种关键性资源需求的最大量应尽可能小,即min{max(g(z))},(g(z))为单位时间里资源占用量。该类优化问题计算出每个排序方案单位时间内关键性资源需求量,并将各方案总工期T内单位时间关键性资源需求量的最大值进行比较,找出最小者对应的工序编排即为最佳方案。
(2)总工期中关键性资源需求的波动幅度尽可能小,即minσ2,σ2为资源占用量的标准方差。该类优化问题计算出每个排序方案总工期内关键性资源需求量的标准方差,找出最小者对应的工序编排即为最佳方案。
(3)综合考虑所需各种资源对完成任务及成本的影响,使之最易实现。该类优化问题实质上是一个多目标优化问题,可通过多资源平衡的归一化处理方法,将其等效为单目标优化问题加以求解。
1.2 求解方法
本文应用MATLAB遗传算法工具箱函数及改进的遗传算法进行求解。
(1)遗传算法的改进策略
在遗传算法中,由于交叉产生的个体是随机的,虽然这种随机化的杂交形式在寻优的初级阶段保持了群体的多样性,但在进化的后期,大量个体集中于某一极值点上时,便造成了近亲繁殖现象。尤其在用遗传算法求解生产调度问题时,经常只能找到个别最优解,甚至是局部最优解。针对这一问题,本文在遗传算法中引入改进策略,有助于查找到更多最优解。
(2)引入最优保存策略
最优保存算法的基本思想是:在计算过程中始终保持所产生的最优点,它不参与交叉运算和变异运算。如果当前代的极优点优于保留的极优点,则用此极优点替换保留的极优点,如果当前代极优点与保留的极优点相同,但是个体不同,则认为多解出现,将此极优点同样保留。
(3)引入子种群迁移策略
多种群遗传算法的个体在种群之间以相同间隔迁移。选择子种群最适应的一部分个体迁移至邻近的子种群中,即最邻近的子种群在他们之间交换个体,均匀地重插入移民个体。这是提高收敛速度的有效方法。
2 计算实例
现有一工程计划,其逻辑关系、工序时间及各工序所需资源如表1所示,要求在工期不改变的情况下,进行如下多资源平衡优化:
(1)施工周期中单位时间内Q资源占用的最大值最小的计划工序(Q资源计划);
(2)施工周期中单位时间内Q资源波动量最小的计划工序(以标准差最小为准);
(3)假设Q、R、S资源对工序的权重分别为0.5,0.2,0.3,求此时单位时间所需资源波动量最小的平衡工序计划。

表1 工序逻辑关系及时间表
2.1 此工序问题模型分析
(1)绘制网络图
根据工序逻辑关系及时间表1绘制的网络计划如图1所示。

图1 网络计划图
(2)计算时间参数
根据表1及图1计算出的时间参数明细表如表2所示。
此资源平衡优化的前提为总工期T固定,因此,工序调整只能选择非关键工序。一般而言,工序Pr(i,j)的时差越大,该工序调整的自由度就越大。在平衡优化时,若将工序调整到时差为零,实际上它已变成关键工序,此时,一旦该工序在施工过程中发生意外,造成施工持续时间延长,这时就会造成总工期增加,造成不必要的损失。由上述表格及网络计划,可进行调整的工序为B、C、E、G、J、L、M、O。
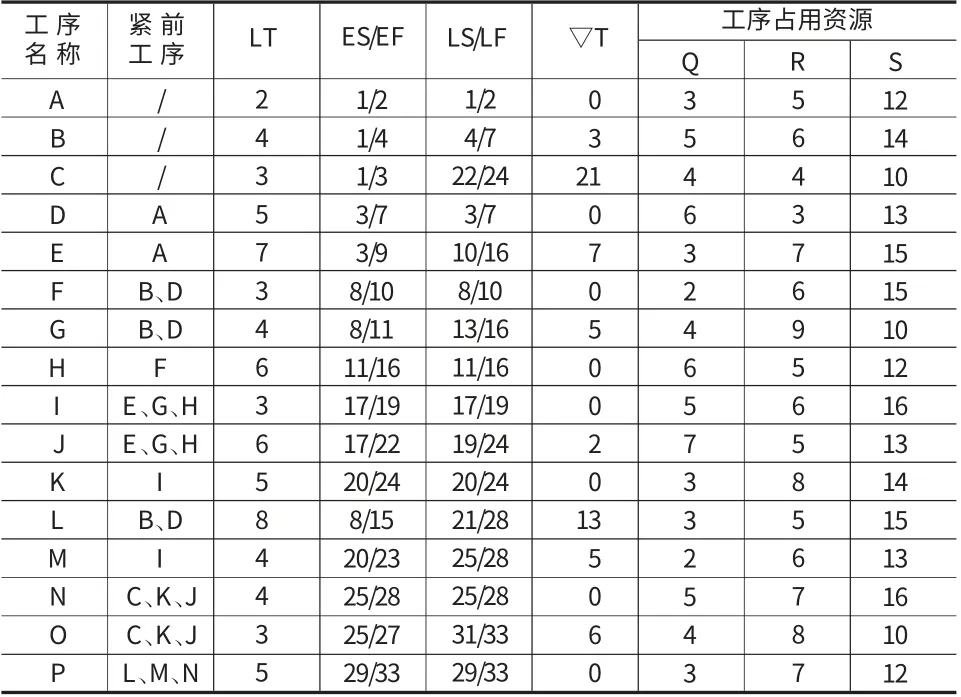
表2 工序逻辑关系及时间参数明细表
2.2 遗传算法的应用
MATLAB遗传算法工具箱提供了广泛多样的有用函数,它使用MATLAB矩阵函数为实现广泛领域的遗传算法建立了一套通用工具,用户可以通过这些命令行函数,根据实际分析的需要,编写出功能强大的应用程序。
(1)初始种群的生成
在整个优化策略中,是以每道工序开工的时间作为设计变量的,由分析可知,实际上的设计变量只有8个,即工序B、C、E、G、J、L、M、O的开工时间,其他工序开工时间为定值。由表2可知,变量可以取的离散值个数为{4,22,8,6,3,14,6,7},在此限定范围内随机产生初始种群,并将其还原为真实的日期。
(2)适应度值评价检测
本文在进行个体适应度评价时,直接用目标函数值作为适应度函数值。MATLAB遗传算法工具箱总是查找适应度函数的最小值,因此一个种群的最佳适应度值就是该种群中任何个体的最小适应度值。
(3)控制参数(GA算子)选择
控制参数的选取对遗传算法的影响很大,但目前对于这些参数的合理选择尚无理论依据,需要根据经验数值和实际计算进行选取。选择较大的初始种群数目可以同时处理更多的解,但是增加了每次迭代的时间,一般种群数目取20~100。本例采用单点交叉方法,交叉率的选择决定了交叉操作的频率,频率越高,可以越快收敛到最有希望的最优解区域,一般选取较大的交叉率,但太高的频率也可导致过早收敛,一般取0.4~0.9。基因变异保证了群体中个体的多样性,较小的变异率不能提供较快的进化速度,较难达到最高的适用度,过大的变异率虽然有助于全局的最优搜索,但也会破坏基因重组产生的优良个体,而需要更多的搜索代数,一般变异率取0.0001~0.1,工艺排序中排序的变异率可选为0.05左右。最大进化代数作为模拟终止条件,取50~500。
(4)改进策略
采用前面设计的最优保存策略和子种群迁移策略。
2.3 求解及结果
根据所采用的策略编程计算,得出如下结果,均有多解,只列出各自其中3个。
问题①对应的工序B、C、E、G、J、L、M、O开工时间 为:1-8-5-11-17-20-25-29;4-1-10-10-17-20-25-30;1-15-5-10-19-20-25-30;目标值为13。
问题②对应的工序B、C、E、G、J、L、M、O开工时间 为 :1-8-5-12-17-21-23-29;1-8-6-13-17-21-23-30;1-8-5-12-17-21-23-31;目标值为2.325。
问题③对应的工序B、C、E、G、J、L、M、O开工时间 为 :1-8-5-12-19-11-25-29;1-8-5-13-19-11-25-31;1-8-5-12-19-11-25-30;目标值为3.645。问题③的计算迭代过程如图2所示。
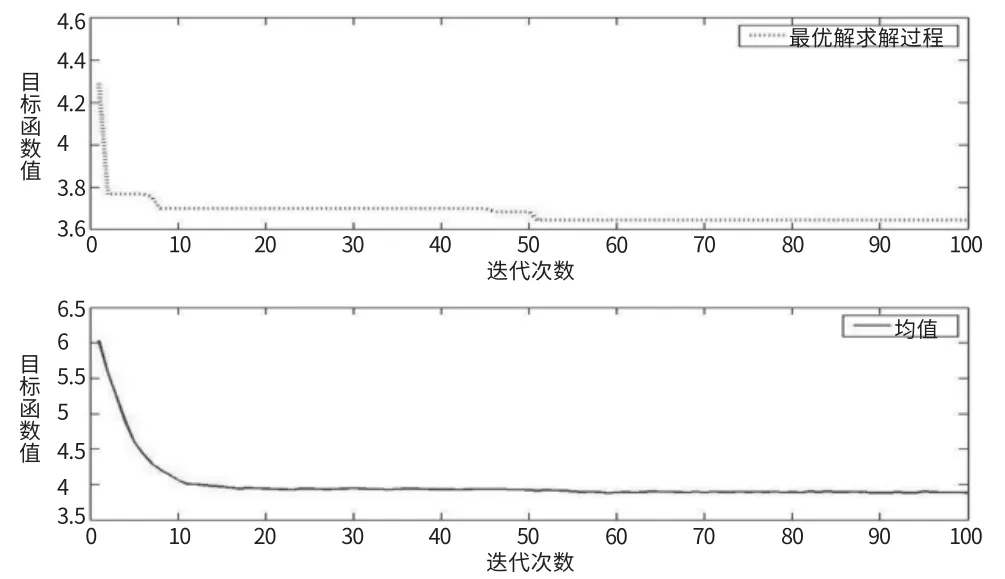
图2 目标值与迭代过程关系图
上述结果①表示采用此种工序编排策略时,施工周期中单位时间内Q资源占用的最大值为13,其他排序方案单位时间内Q资源占用的最大值均不小于13。结果②表示施工周期中单位时间内Q资源的波动量即标准方差最小为2.325;结果③表示按题设权重对Q、R、S三种资源进行归一化处理后,此时求得单位时间内所需资源量标准方差的最小值为3.645。所考虑的优化问题均有多解也从另一个方面说明了大量工序排序问题方案的不唯一性。
3 结论
本文建立了多资源平衡工序优化的数学模型,其建模过程简洁、明了。实例的工序问题,每类优化决策问题就有4*22*8*6*3*14*6*7=7451136种排序方案,采用改进的遗传算法进行计算,不同的问题只须对功能函数稍作改变很快就可得出结果。通过引入最优保存策略和子种群迁移策略,本文克服了传统遗传算法中的过早收敛和局部搜索能力差问题,大大提高了搜索效率和收敛速度,并且获得了多组最优工序计划(也从另一个方面说明了大量工序排序问题方案的不唯一性),这使得生产调度安排灵活机动,便于智能调度。
[1]杨永清.网络计划多资源平衡优化工序排序方法研究[J].湖南轻工业高等专科学校学报,2003,15(3):5-7.
[2]何文章,宋 维.基于改进混合遗传算法安排生产调度[J].数学的实践与认识,2007,37(4):1-4.
[3]戴建国.活动网络资源均衡问题及其遗传算法[J].系统工程学报,1996,11(2):29-36.
[4]牛东晓,乞建勋.工程网络资源平衡的改进型遗传算法研究[J].华北电力大学学报,2000,27(3):1-5.
[5]周国华.遗传算法及其在生产调度中的应用[J].西南交通大学学报,2000,1(2):36-39.
[6]雷英杰,张善文,李续武等.MATLAB遗传算法工具箱及应用[M].西安电子科技大学出版社,2005.

