基于自适应扩展卡尔曼滤波器的永磁同步电机超低速控制*
丁信忠, 张承瑞,2, 李虎修, 于乐华, 胡天亮,2
(1.山东大学机械工程学院,山东济南 250061;
2.山东大学高效洁净机械制造教育部重点实验室,山东济南 250061;
3.山东大学控制科学与工程学院,山东济南 250061)
0 引言
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)精确的速度及位置反馈是实现高性能低速控制的重要保证。通常,借助轴向编码器的采样计数估算出电机的平均速度。但是,受到编码器分辨率的限制,在超低速范围,速度反馈信息容易丢失,如果通过延长采样周期以保证速度分辨率,将降低速度环的带宽,且过长的反馈延时将使伺服系统变得不稳定。
目前,瞬时观测器理论[1]和人工神经网络[2]被深入研究,并应用于伺服系统状态估计。基于瞬时观测器理论的状态估计方法能够估计电机的瞬时状态,具有较好的实时性,但抗干扰能力不佳,在噪声环境中,位置和速度检测可能失效[3]。人工神经网络方法摆脱了对电机模型的依赖,具有良好的鲁棒性,但需要大量样本对神经元的权值和偏置进行训练,学习时间过长,而且网络的稳定性和收敛性的证明也比较困难[4]。扩展卡尔曼滤波器(Extended Kalman Filter,EKF)是一种最优随机状态估计器,可对非线性时变系统的状态进行在线估计,并具有较强的抗干扰和平滑噪声能力,因而适用于非线性、强耦合且高噪声的伺服驱动系统。随着嵌入式计算技术的发展,EKF计算量大的问题已被良好解决。
本文提出了一种使用低精度编码器条件下获得PMSM良好低速性能的控制方法。其中,EKF用于对电机转速、角位移和负载转矩进行瞬时估计,并在估计过程中利用辨识出的敏感参数对估计器的状态矩阵进行迭代修正,以保证估计器在多种工况下均可获得满意的估计结果。估计出的电机瞬时转速和位置值替代编码器检测值进行伺服闭环控制,由此保证电机低速运行下的转速和位置反馈精度。为验证该方法的有效性,本文设计仿真和试验与使用改进型M/T速度检测方法[5]下的低速控制性能进行了对比。
1 EKF瞬时状态估计器
1.1 估计器建模
在未饱和状态下,PMSM的电压方程为
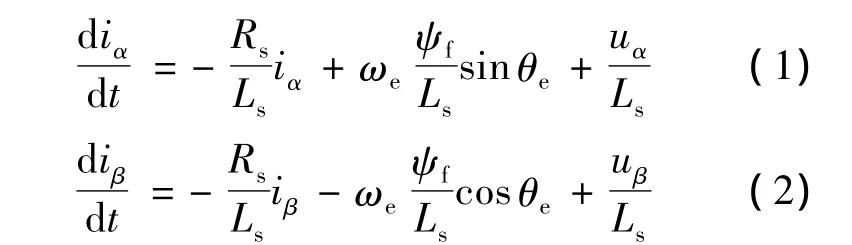
式中:iα、iβ、uα和uβ——分别为定子电流、电压在Clarke坐标系下α、β轴的分量;
Rs——定子相电阻;
Ls——等效同步电感;
ψf——永磁体基波磁链;
ωe——转子电角速度;
θe——电角位移。
转子和所带负载组成机械子系统,根据牛顿定律,可得PMSM的转矩平衡方程为
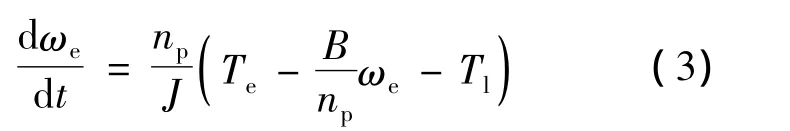
式中:np——电机极对数;
J——系统转动惯量,其中包括电机转子及负载折算到电机轴上的转动惯量;
B——黏滞摩擦系数;
Te——电机输出的电磁转矩;
Tl——等效负载转矩,其中包括负载转矩以及由于黏滞摩擦系数非线性变化、电流给定偏差等因素造成的转矩波动。
由于电流环的采样频率远高于等效负载转矩变化的频率,故可认为负载转矩在一个采样周期内保持不变,即

联合式(1)~式(4),得到状态估计器的状态方程和输出方程,即
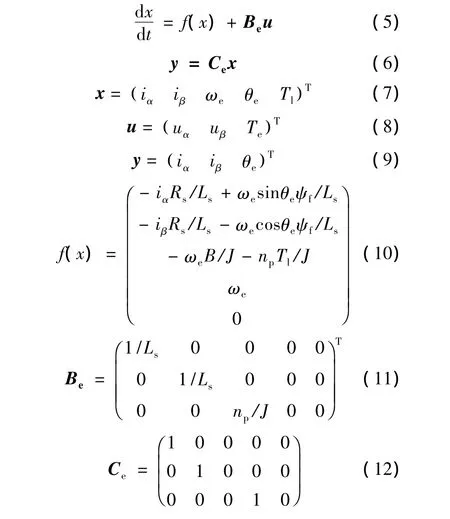
式中:x——状态矢量,即预估计量;
u——输入矢量;
y——输出矢量。
状态函数f(x)是状态矢量和输入矩阵的耦合项。
实际系统中,需要考虑由于估计模型不准确和外界干扰等不利因素造成的影响,因此在EKF的状态方程和输出方程中分别引入系统噪声矩阵V和测量噪声矩阵W,并将估计方程离散化以便用于数字控制系统,可得
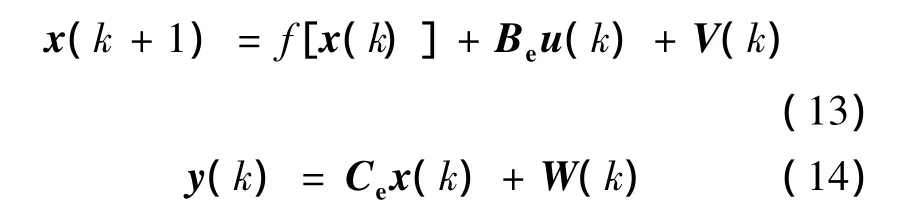
式中:x(k)、u(k)、y(k)和f[x(k)]——分别为状态矢量、输入矢量、输出矢量和状态函数的离散形式;
V(k)和W(k)——分别为离散化的系统噪声矢量和测量噪声矢量。
通常,系统噪声和测量噪声为零均值高斯白噪声,由此可得到EKF算法中需要的噪声协方差对角矩阵Q和R,即
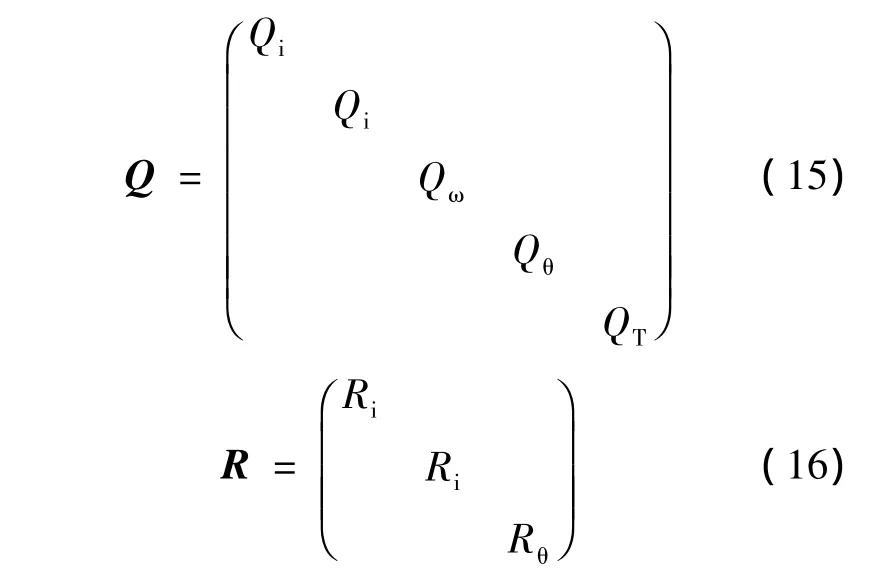
式中:Qi——定子电流系统噪声协方差值;
Qω、Qθ和QT——分别为转子电角速度、电角位移和负载转矩的系统噪声协方差值;
Ri——定子电流测量噪声协方差值;
Rθ——转子电角位移测量噪声协方差值。综合以上各式,即得到用于EKF伺服系统状态估计的状态模型。
1.2 EKF状态估计与鲁棒性分析
基于EKF的伺服系统状态估计是由第k次的估计结果(k)来获得第k+1次的估计结果,即由当前的系统状态来估计下一周期的状态,从而解决了M/T速度检测方法速度反馈滞后一个周期的问题,加之算法中综合考虑了系统噪声和测量噪声的影响,因此可以为伺服闭环控制系统提供实时、准确的状态反馈,有助于提高伺服系统的动、静态性能。
估计过程分为预测和校正两大阶段,通过以下递推过程[6]逼近系统真实状态:
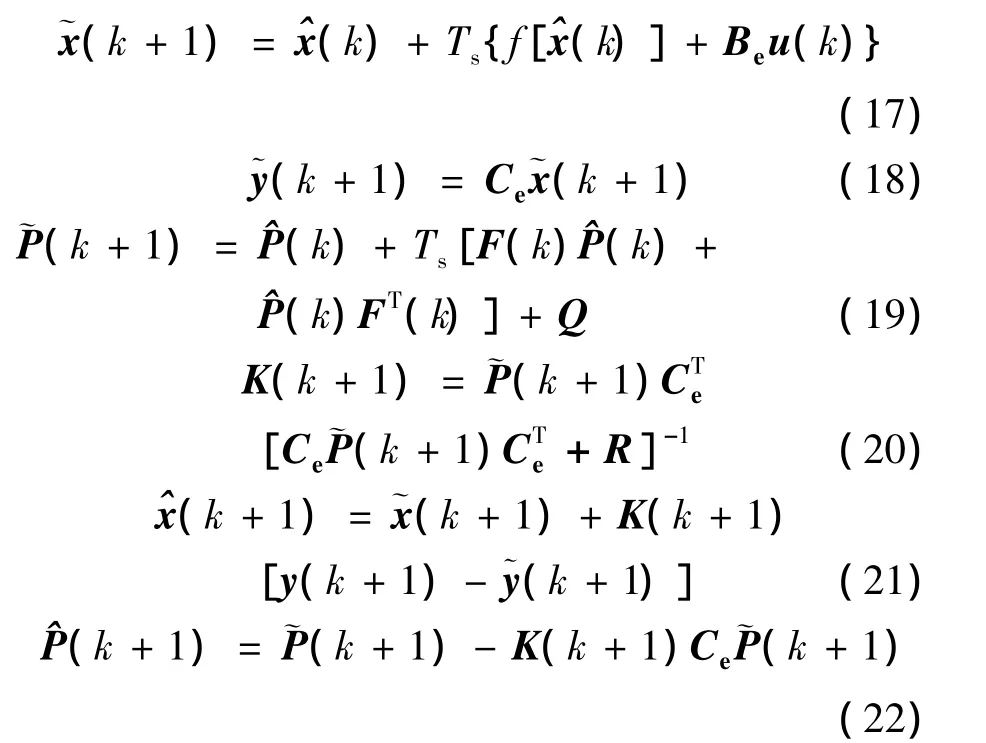
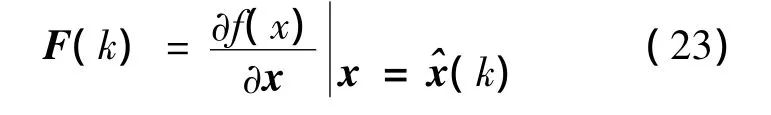
经过以上6个步骤的递推计算,即可得到本周期内的状态矢量中的预估计变量值,基于EKF的伺服系统状态估计过程如图1所示。
式中:Ts——电流环采样周期;
˜
P˜(k)和P^(k)——分别为预测协方差矩阵和估计协方差矩阵。
F(k)为梯度矩阵,定义如下:
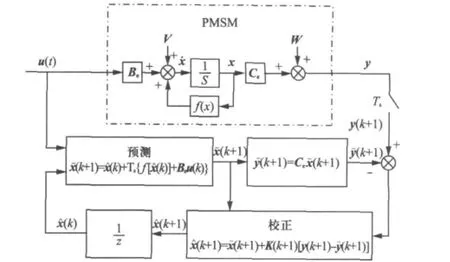
图1 离散扩展卡尔曼滤波器结构图
当电动机在零速附近运行时,绕组电压将降到很低,此时电机定子电阻、等效电感及系统转动惯量J等因素将对系统动态模型产生主要影响,从而影响EKF的估计效果。但是,EKF的系统模型中综合了定子电流采样这一因素,在超低速区域,霍尔电流传感器依旧可以提供准确的电流反馈,从而弥补了绕组电压过低产生的影响。当负载转动惯量变化时,EKF的动态性能将相对降低,文献[7]中指出,无法将转动惯量变化引起的转矩脉动等价到等效负载转矩Tl中,通过转矩前馈加以改善,且无法通过调整系统噪声矩阵中转矩协方差值QT来减小转动惯量变化对估计精度的影响。
为解决上述问题,在伺服系统状态估计中,需要对系统的转动惯量进行在线辨识,并根据辨识结果对EKF的状态方程系数矩阵进行在线参数自整定。
2 转动惯量在线辨识
对于表贴型永磁同步电机,将式(3)所示的转矩平衡方程改写为
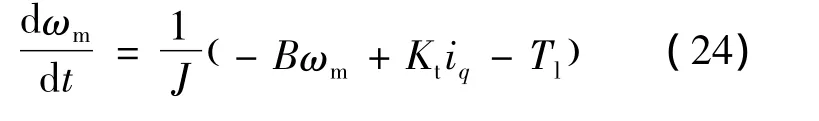
式中:ωm——转子机械角速度;
Kt——转矩常数;
iq——交轴电流。
令J'=1/J,T'=Ktiq-Tl,式(24)可简化为
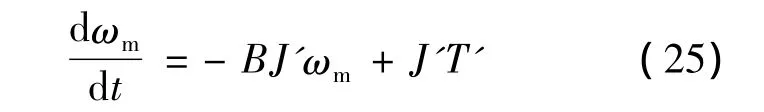
式(25)中包含待辨识参数J的信息,且与PMSM具有相同的外部激励输入iq以及相同的机械转速ωm输出。将ωm和J'分别以其估计值^ωm和J^'表示,可得模型参考自适应系统(Model Reference Adaptive System,MRAS)可调模型的微分方程:
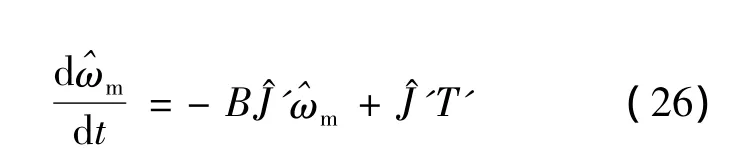
选择PMSM本身作为参考模型,式(25)为表征参考模型动态特征的差分方程,当方程(26)中的估计值与实际值相等时,差分方程(26)就转变为表示PMSM本身的真实方程,两个模型将等价。待辨识参数J^'为MRAS状态变量,将参考模型的差分方程(25)减去可调模型(26),可得
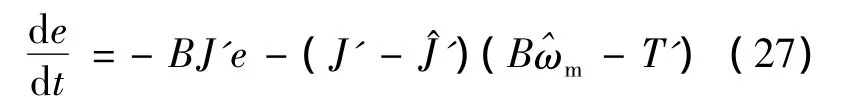
式中,e为广义误差,定义如下:

对于数字控制系统,伺服电机的电气时间常数远小于其机械时间常数,故在一个速度环控制周期内,假定转子机械转速ωm和系统转动惯量J不变。根据式(27),MRAS辨识系统可等价为一个标准反馈系统,其中包含一个线性时不变前馈子系统和一个非线性时变反馈子系统。
MRAS的关键问题之一是自适应机构中所执行的自适应规律的确定。自适应规律保证广义误差渐近稳定且待辨识参数收敛到真实值[8]。根据Popov超稳定理论,若保证自适应系统稳定,其中的非线性时变反馈环节需要满足
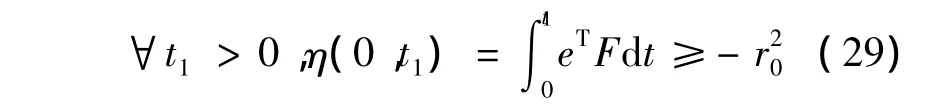
其中,F=()();是当t1>0时不随时间变化的有限正数。
为了避免广义误差趋近于零时算法失效,自适应规律通常设计为比例积分(PI)结构。因此,将预估计量J^'的自适应规律取为PI形式,即
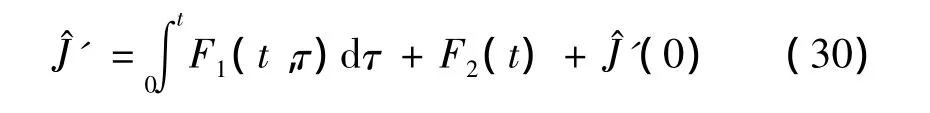
式中,(0)为初始值。将F和式(30)代入式(29),经推导可得自适应规律:

结合式(27),MRAS转动惯量辨识系统的等效非线性结构如图2所示。依据自适应规律,状态变量驱动可调模型趋向于参考模型。因此,在广义误差趋近于零的过程中待辨识的转动惯量将逐渐趋近于真实值。
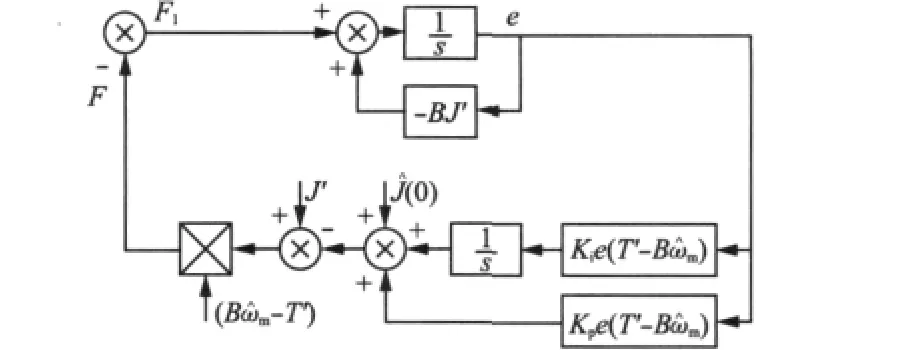
图2 MRAS参数辨识等效非线性反馈系统
MRAS辨识出的转动惯量用于在线更新EKF状态估计器的系统矩阵,从而实现转动惯量的鲁棒控制。EKF估计出的状态变量中,角速度^ωm和角位移θ^m分别用于速度环和位置环的反馈值,等效负载转矩T^l用于前馈控制以消除电机转矩脉动。将转动惯量自适应EKF状态估计用于PMSM伺服驱动系统,构成带有速度估计和转矩前馈的速度伺服系统,如图3所示。
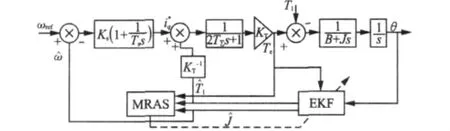
图3 EKF状态估计速度伺服系统
3 仿真及试验分析
仿真和试验中所用PMSM及所带负载的参数如表1所示。图4显示了不同转动惯量初始值下的转动惯量辨识结果,其间速度指令和转矩指令分别在0.15 s和0.3 s时刻阶跃变化。可以看出,惯量辨识值快速收敛于真实值,且在转速和转矩突变时没有发生振荡。
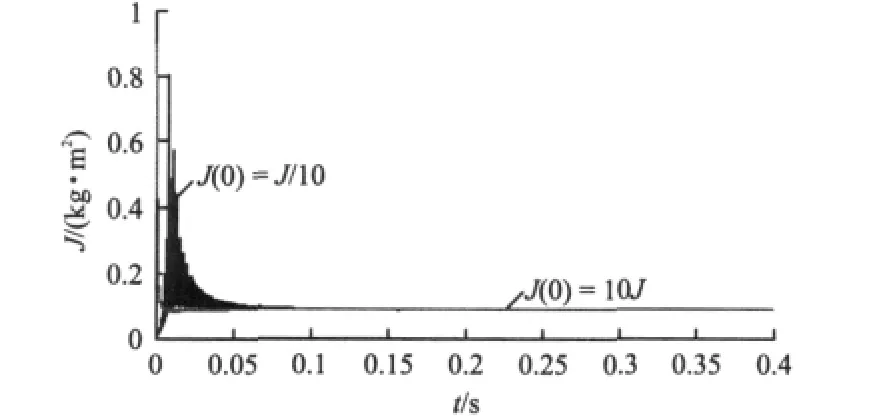
图4 阶跃指令下不同初始值的惯量辨识效果
图5所示的仿真试验中,设定速度指令为±100 r/min,负载转矩恒定在8 N·m。在0.5 s时刻将EKF输入矩阵中定子电阻修改为准确值的2倍,而同步电感为准确值的1/2,并在1 s和2 s时刻分别将转动惯量设定为真实值的2倍和1/3。从仿真结果可以看出,当定子电阻和等效电感取值不准确时,估计器并未受到影响。相比之下,从仿真结果可以看出,当EKF系数矩阵中转动惯量的取值偏离准确值时,电机转速和转矩的瞬态估计结果将出现较大的超调和波动。由此可见,EKF估计器对转动惯量较为敏感,而对电阻和电感具有较好的鲁棒性。在实际系统中,需要利用转动惯量辨识结果对EKF的系数矩阵进行在线整定。

图5 被控对象电气参数对估计结果的影响
本文所用试验系统如图6所示。电机同轴安装一个SICK公司生产的32 768线高精度光电编码器,并连接至专用控制器捕捉倍频后的编码器脉冲,测量电机的实时转速,作为比对参考。其中,速度环和电流环的控制周期分别设定为400 μs和 80 μs,得益于 STM32F4 处理器的强劲性能,转动惯量辨识、EKF状态估计以及PI电流控制器的总计算时间约为30 μs,加上约20 μs FOC算法执行时间,所有的电机控制算法可在一个电流环周期内执行完毕。

表1 仿真和试验中所用电机参数
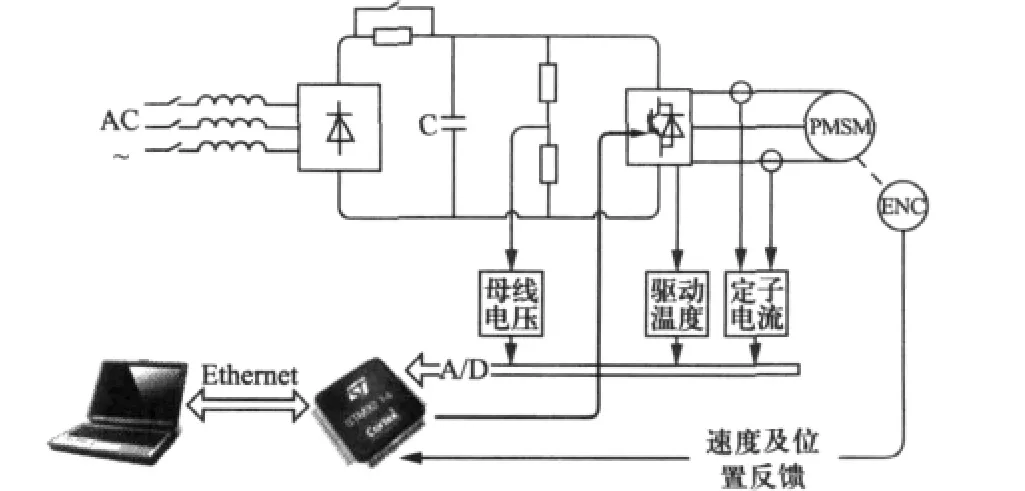
图6 试验平台配置
图7所示试验结果对比了超低速下使用转动惯量自适应状态估计器ωest和M/T速度检测ωenc方法时的电机速度响应。试验结果表明,在超低速度下,由于编码器反馈信息的缺失,使用M/T方法时的速度响应趋于不稳定。相比之下,本文提出的方法仍旧能够提供准确的速度反馈,获得良好的低速控制性能。
图8所示为动态转速响应的对比波形。试验中,速度给定ωref为频率70 Hz,幅值20 r/min的正弦指令。使用编码器检测转速作为速度反馈时,速度响应ωenc存在约30°的相位滞后,而使用自适应EKF速度估计作为速度反馈值时,速度响应ωest没有明显的相位滞后,动态跟随特性良好。

4 结语
本文提出了一种使用常规编码器条件下获得PMSM良好速度特性的控制方法。仿真和试验结果表明,当PMSM运行于低速或超低速区域时,本文提出的EKF状态估计策略依旧可以提供准确、实时的速度反馈,从而在宽调速范围内实现良好速度控制性能,有效改善了系统的动态性能并增大了调速范围。此外,通过MRAS在线辨识出的转动惯量对EKF系数矩阵实施自整定后,自适应EKF估计算法对系统转动惯量、定子电阻、等效电感的变化以及环境噪声均有很好的鲁棒性,与使用M/T速度检测方法相比具有调速范围宽、实时性好及抗干扰能力强等优势。
[1]WANG M S,KUNG Y S,THI H,et al.Superior low-speed control of a permanent magnet synchronous motor with digital encoder[C]∥Proceedings of the Institution of Mechanical Engineers,PartⅠ:Journal of Systems and Control Engineering,2011,225(2):281.
[2]KARANAYIL B,RAHMAN M F,GRANTHAM C.On-line stator and rotor resistance estimation scheme for vector-controlled induction motordriveusing artificial neural networks[C]∥Industry Applications Conference,2003,38th IAS Annual Meeting,2003:132-139.
[3]HEUI W K,SEUNG K S.A new motor speed estimator using Kalman filter in low-speed range[J].Industrial Electronics,IEEE Transactions on,1996,43(4):498-504.
[4]杨晓帆,陈廷槐.人工神经网络固有的优点和缺点[J].计算机科学,1994(2):23-26.
[5]杨松涛,和丽清,安成斌.DSP在高精度数字式电机测速中的应用[J].红外与激光工程,2006(S4):543-548.
[6]王成元,孙宜标,夏加宽,等.电机现代控制技术[M].北京:机械工业出版社,2006.
[7]TAEG J K,DONG S H.High-performance speed control of electric machine using low-precision shaft encoder[J].Power Electronics,IEEE Transactions on,1999,14(5):838-849.
[8]ATTAIANESE C,DAMIANO A,GATTO G,et al.Induction motor drive parameters identification[J].Power Electronics,IEEE Transactions on,1998,13(6):1112-1122.

