永磁同步电动机步进控制动态特性研究
刘 斌, 李小庆, 董 砚, 郑 易
(河北工业大学控制科学与工程学院,天津 300130)
0 引言
20世纪80年代,永磁材料特别是高磁能积、高矫顽力、价格低廉的钕铁硼永磁材料的发展,使人们研制出了价格低、体积小、性能高的永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)。PMSM以其高效率、高转矩惯量比、高能量密度而受到诸多关注,因而在数控机床、军工、航天等领域逐渐得到广泛应用[1-2]。
交流步进传动控制是把位置控制、速度控制和伺服控制等不同的传动控制方式有机地结合起来,使同步电动机的气隙磁动势由连续的旋转磁场变为离散的步进磁场。对离散的步进磁动势进行控制,可以获得良好的速度控制,还可进一步取得精确的位置控制,从而形成高性能的交流传动控制系统。电力电子技术的应用使系统具有离散控制的基本特征,使传统的运动控制思想得到突破。它打破了连续与离散、速度与位置、旋转与步进的严格界限,形成了一种统一的交流步进控制理论[3]。
本文主要针对交流步进控制的典型控制方式——恒频控制,进行了动态仿真研究及试验验证。
1 交流步进控制和恒频控制
1.1 交流步进控制
同步电动机的步进控制中心思想是将电动机的定子电流离散为bH步。每一步对应一个大小固定和位置步进的定子磁动势,与转子磁动势构成步进角,产生步进的复位转矩,从而将转子锁定在一个特定的位置上。
如果将同步电动机的定子磁势由旋转磁势离散为步进磁势,则定子气隙中所停靠的位置也就是这种电机步进运动时能够提供的定位点数,即电机的每步数。
当PMSM定子绕组通以三相对称正弦电流ia、ib、ic时:
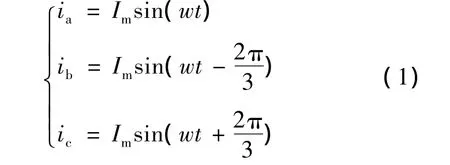
式中:Im——通入的三相电流的峰值。
将PMSM三相磁动势进行合成可知,三相绕组产生的气隙磁动势是一个旋转磁动势,其幅值是相脉振磁动势幅值的1.5倍:
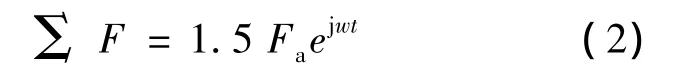
式中:Fa——相脉振磁动势的幅值。
若按电角度计算,旋转磁动势在空间运行的电角度θ和绕组中电流在时间上经历的电角度永远相等,即

旋转磁动势每秒钟的转速为

式中:f——定子电流的频率;
pm——电动机的磁极对数。
假设对于三相定子绕组,如果不通入连续正弦电流,而是输入下列对称的离散电流:
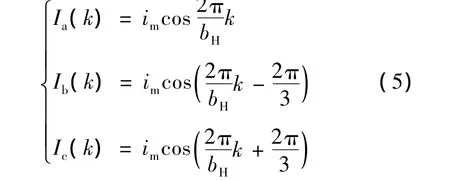
式中:im——通入的相电流峰值;
bH——环形分配器的循环拍数;
k——主令脉冲的拍数。
将输入电流的一个周期分为bH份(bH为正整数),对于三相绕组,为了保证三相电流互差2π/3和各相的正负半周对称,最好取bH是6的整数倍。k为主令脉冲的拍数,它等于任意正整数。由此得到的气隙磁动势将是一个步进磁动势:
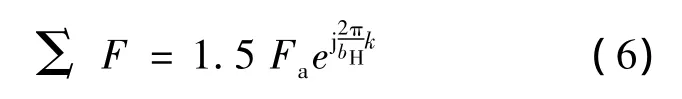
PMSM以定子电流为直接控制对象,模拟步进电机的运动控制模式,进而将电流矢量离散,根据提前给定的电流步数即可获得不同的转矩,并且还可以获得较好的定位性能,实现增量运动。
1.2 恒频控制
步进传动有多种典型控制方式,包括:点动运动、恒频、升降频、最优控制等。其中小容量步进传动常采用恒频控制方法,因为它对计算机的要求低,特别适用于多机控制。在这种控制方法中,计算机用恒定的频率输出电动机所需要行进的步数,只要这个频率低于突跳频率,不会造成步进传动丢步即可[4]。实际应用的突跳频率是通过试验反复试探得到的。
恒频运动的数学描述如下。
恒频运动时,定子电动势的位置角为θs,它每步过跨进电角度θb,转子前进的角度为θr。电磁转矩为[1]
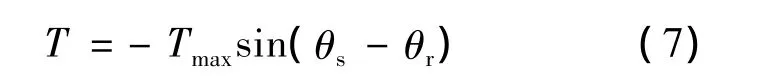
阻尼转矩和定子磁动势与转子的相对运动速度成正比。阻尼转矩表示为
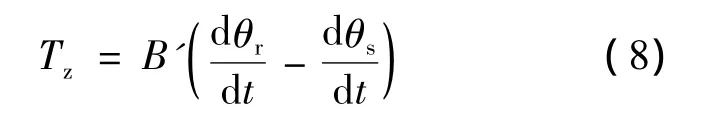
恒频控制的动态方程为
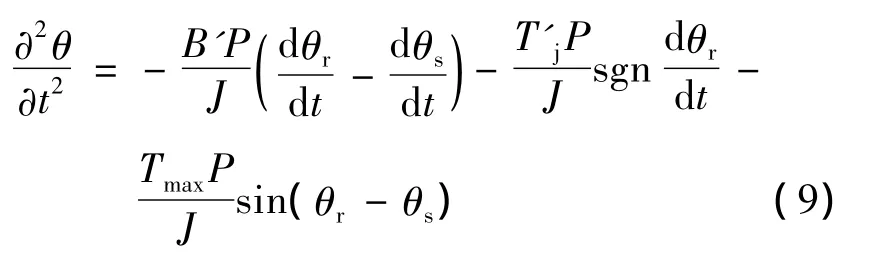
恒频控制中有两种抖动现象:一是电动机起动到稳速围绕稳定转速产生的追逐现象,这和普通电动机起动产生的转速超调和振荡很相似,一般情况是允许的;二是抖动现象出现在停车时,停车时出现的抖动现象和点动时属于同一类型,因为只看最后一拍也就是一种点动。加入砰-砰控制,可以消除恒频控制中停车产生的抖动现象。可以肯定在恒频控制中不会出现丢步现象,因为丢步是不允许的,选取的工作频率保证了这一点。从这一前提条件出发可以得出结论;恒频控制中最后一拍产生的位置超调量,最大也只能等于允许的最大动态角误差。
2 仿真模型与试验平台搭建
2.1 仿真模型搭建
系统MATLAB/Simulink仿真模型主要包括:电流滞环PWM逆变器模块、PMSM模块、电动机测量模块、MATLAB功能函数模块等几部分[5-6]。其工作原理为通过电机测量模块获得电动机转子的位置和速度参数,并将其反馈到MATLAB功能函数模块,经过MATLAB函数模块和逆变模块将连续正弦电流离散化,形成步进电流。反馈部分通过测量电动机的实际电流值与给定电流相比较,用电流滞环模块实现电动机的自动控制,从而获得良好的动态特性。
2.2 试验平台搭建
搭建了全数字驱动控制器的PMSM传动系统,控制器由DSP控制部分和驱动功率放大部分组成。控制部分的核心芯片采用TI公司的DSP芯片TMS320F2407A,主要包括:DSP外围电路,电流信号的电压提升电路,位置检测电路,显示按键驱动电路;功率放大部分的核心模块为三菱公司的IPM智能功率模块PM15RSH120,主要包括:多组独立电源,触发信号驱动电路,电压、电流采样电路,保护电路。控制系统硬件结构图如图1所示。
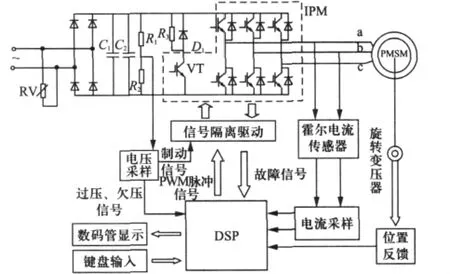
图1 控制系统结构框图
驱动控制器的主电路由整流电路、直流中间电路和逆变电路三部分及有关的辅助电路组成。
主电路原理图如图2所示。
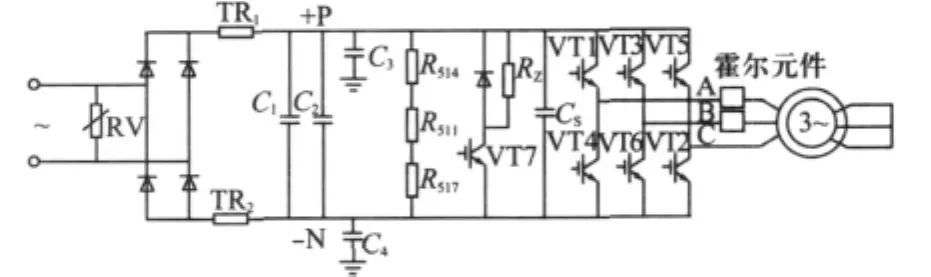
图2 电压源型逆变器主电路
此外,系统采用了抗干扰能力较强的旋转变压器作为位置传感器,同时还设计了电流检测单元。在电动机控制中,由于电动机采用三相三线制的接线,故三相定子电流的检测,只需检测其中两相即可,另一相可由其他两相获得。
3 仿真和试验结果
3.1 仿真结果
恒频控制下PMSM的起动过程是,在ε角增到180°之前,只要复位转矩已迫使转子升速到突跳速度ωrT,ε就会保持在180°之内,并一直升速到 ωr> ωrT,几经振荡后,进入 ωr= ωrT、θ=0°、ωs=ωr的稳定区。这就是恒频控制电动机起动的过程描述。从理论分析可知,用恒频控制方法起动电动机不会出现失步现象,为了保证这一点要求,选取了一定的工作频率。恒频控制中最后一拍产生的位置超调量,最大也只能等于允许的最大动态角误差。
PMSM模型主要参数设定如下:极数为4极,相绕组 2.48 Ω,交、直轴电感分别为 0.038 H,扭矩4.8 N·m。恒频控制方式定子电流仿真曲线如图3所示。
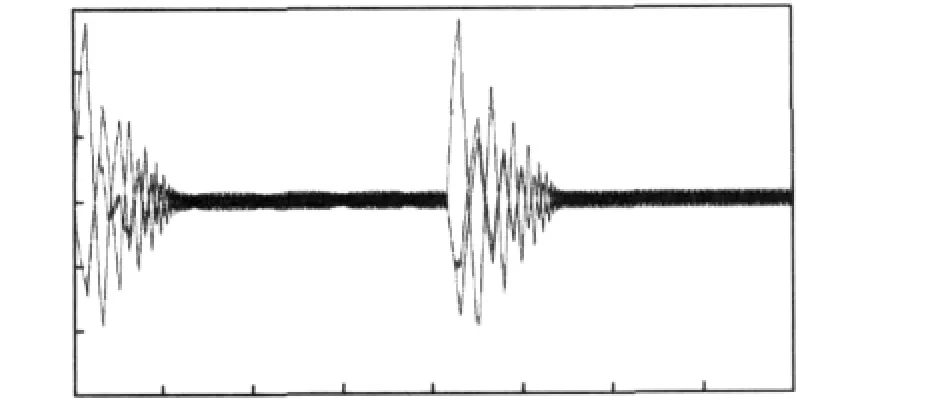
图3 恒频控制方式定子电流仿真曲线
恒频控制方式下电机的速度、位置仿真曲线如图4所示。
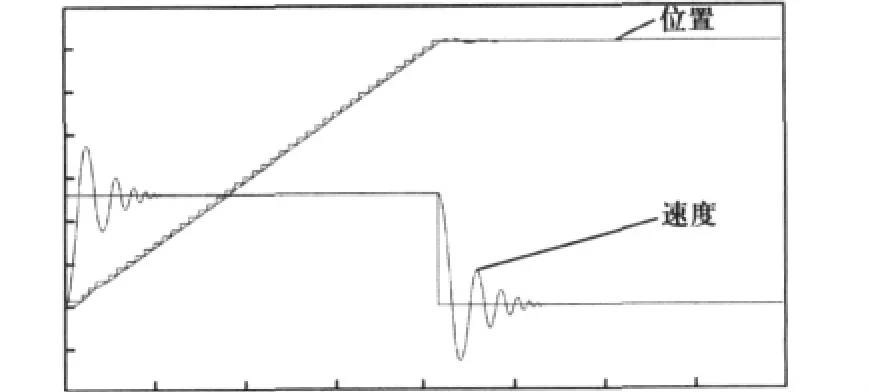
图4 恒频控制方式下电机的速度、位置仿真曲线
恒频控制方式下电机的转矩仿真曲线如图5所示。
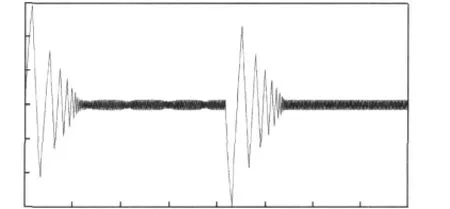
图5 恒频控制方式下电机的转矩仿真曲线
3.2 试验结果
在恒频控制中要保证不丢步的情况下,选取合适的工作频率,这里为了使恒频控制过程更加清晰,选择较小的工作频率1 Hz,从图6和图7可看出,转子位置随着给定电流矢量步数一步一步跟随,获得很好的离散控制的定位特性。位置响应曲线见图8。
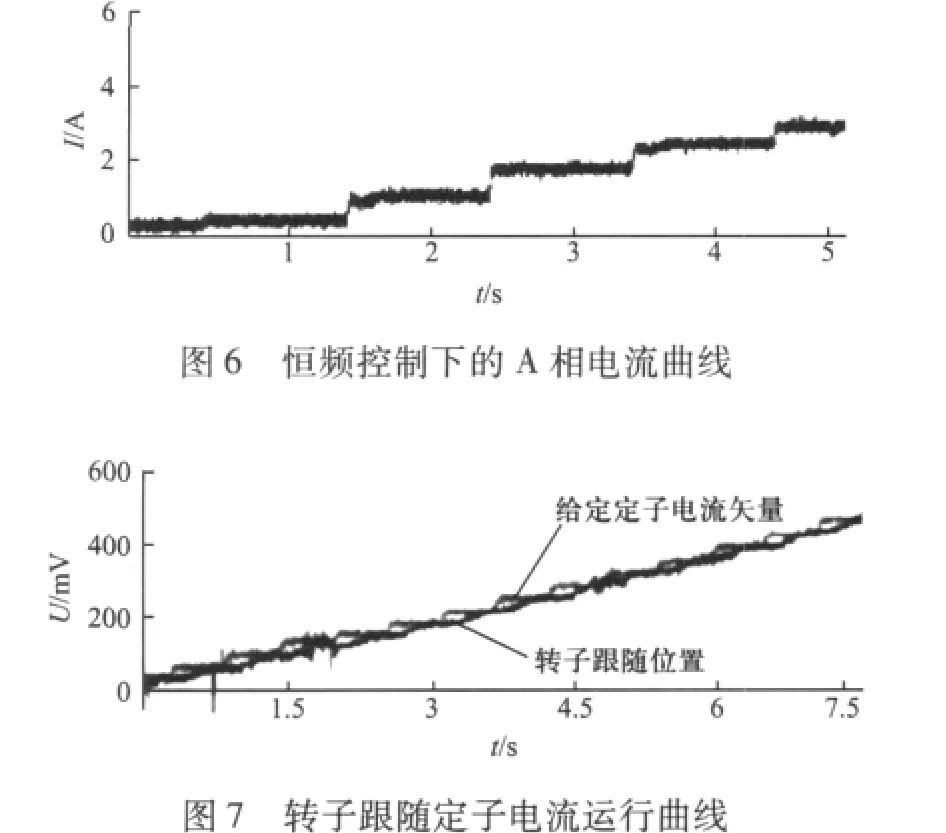
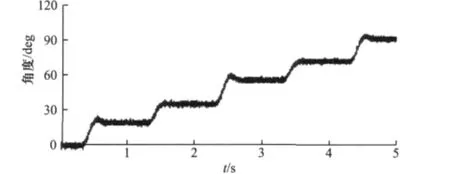
图8 恒频控制下的位置响应曲线
4 结语
基于恒频控制的PMSM系统以一种恒定频率去起动电机,线路简单,从而降低了成本。通过MATLAB仿真和试验验证,基于恒频控制的PMSM具有良好的动态特性,完全可以满足现实中对于速度及定位精度的要求,本文对于PMSM在高性能控制场合下的应用提供了参考。
[1]孙鹤旭.交流步进传动系统[M].北京:机械工业出版社,1996.
[2]顾绳谷.电机及拖动基础[M].北京:机械工业出版社,2004.
[3]王晓军.交流步进传动及离散控制的研究[D].天津:河北工业大学,2003.
[4]陈伯时,谢鸿鸣.交流传动系统的控制策略[J].电工技术学报,2002,15(5):11-15.
[5]常红军.交流传动系统PSpice与Matlab仿真技术的研究[D].天津:河北工业大学,2006.
[6]林飞,杜欣.电力电子应用技术的MATLAB仿真[M].北京:中国电力出版社,2009.

