三相电压型高频PWM整流器的LCL滤波器研究与设计
赵文华, 刘 勇, 韩素芳
(1.海军驻上海江南造船(集团)有限责任公司军事代表室,上海 201913;
2.上海电器科学研究所(集团)有限公司,上海 200063)
0 引言
三相电压型高频PWM整流器,因其能够同时控制直流电压[1]和电网侧的功率因数而被广泛应用到电机驱动、蓄电池放电控制,以及分布式并网发电系统中[2]。但系统中开关管工作于高频方式,会在电网侧产生高次谐波。采用传统的L滤波器会带来一些问题,如为了得到较好的滤波效果必须增大滤波电感L的值,这样就会增加系统的投资,并且大电感的体积也较大。采用LCL滤波器能够很好地滤除高次谐波,并且在同样的谐波要求下,相对于L滤波器[3]可以很大程度地降低滤波电感的阻值大小,提高了系统的稳定性。
1 LCL滤波器和L滤波器性能的比较
LCL滤波器的高频PWM整流拓扑结构如图1所示。
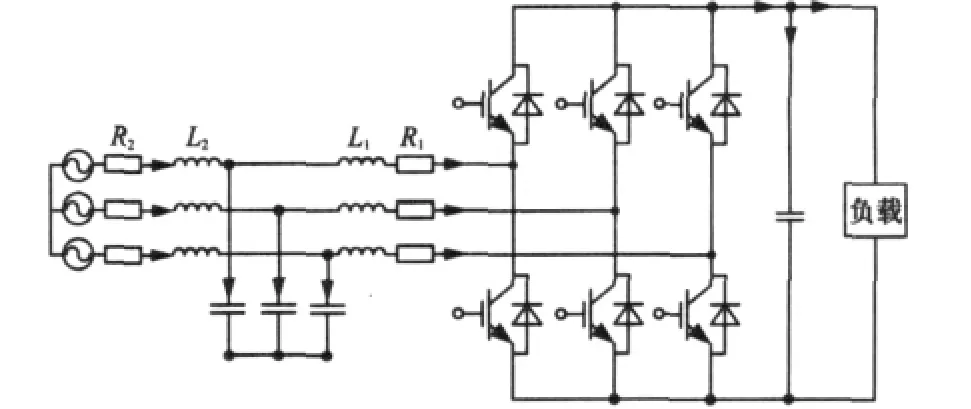
图1 基于LCL滤波的高频PWM整流器拓扑
取单相的电路进行分析(滤波电感的电阻值非常小可以忽略),可以得到网侧电流和整流器交流侧电压的关系式如下。
LCL滤波器拓扑结构中[4]:
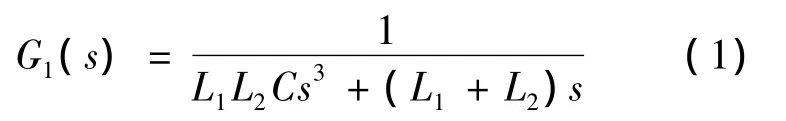

取LCL滤波器整流侧电感值为1.2 mH、网侧电感值为0.8 mH,L滤波器电感值为2.0 mH。利用MATLAB绘制式(1)及式(2)的波特图,如图2所示。
L滤波器拓扑结构中:
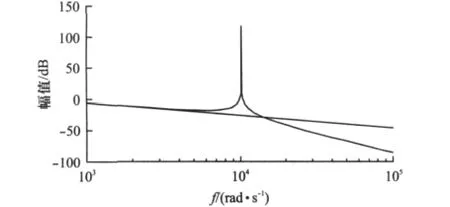
图2 G1(s)及G2(s)波特图
由上面的两种不同滤波器的传递函数形式,并结合使用MATLAB绘制的幅频特性曲线图可知,低频段时LCL型滤波器具有和L型滤波器相同的特性。高频段时,LCL滤波器具有更高的衰减速度,因此它能够很好地滤除逆变器产生的高频谐波。但是LCL滤波器存在谐振,在其谐振频率处的谐波非但没有得到衰减,反而得到了很大的加强。这点是需要解决的问题。
2 抑制LCL滤波器谐振的方法
由LCL滤波器的传递函数可知,其之所以出现谐振,是因为它是一个三阶的无阻尼系统。因此一般的抑制系统谐振的方法有两种:无源阻尼法[5]和有源阻尼法[6-7],前者是通过在电容或电感上串联或者并联阻尼电阻来实现抑制谐振的目的,后者是通过修正算法使系统达到稳定,消除谐振。无源阻尼法能够有效抑制谐振,但是阻尼电阻的加入会使系统的损耗增大,降低了系统的效率。有源阻尼法是通过算法实现的,不会产生硬件损耗,但是需要额外增加测量电容电压或电流的传感器,系统的投资变大了并且程序算法也更加复杂了。实际应用中应综合考虑各方面的因素选择最合适的方法。
3 LCL滤波器的设计
LCL滤波器的设计应该考虑到如下因素:(1)设计的LCL滤波器能够有效滤除网侧电流中的高次谐波,使其满足相应的标准。
(2)LCL滤波器中的滤波电容吸收的无功功率应低于额定功率的5%[2],确保系统具有较高的功率因数。
(3)为了有效滤除开关频率附近的谐波,系统的谐振频率不应取的过高,但是也不能过低,避免较低次的谐波得到放大,一般使其介于10倍的基波频率和0.5倍的开关频率之间[2]。
(4)应该考虑是否加入阻尼电阻来抑制LCL滤波器的谐振,使系统稳定。
LCL滤波器设计时,首先根据纹波要求计算总的电感量;然后由电容吸收的无功量来计算出滤波电容C的大小;最后利用谐振频率和谐波抑制比作为中间变量,分别得到网侧和变换器侧的电感值大小。
3.1 总电感L的设计
只考虑纯电感滤波的PWM整流器,稳态情况下整流器交流侧的矢量关系如图3所示。
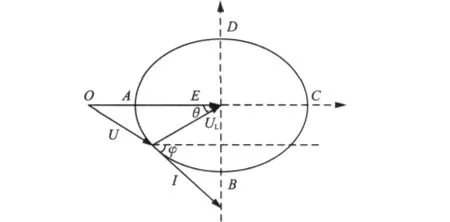
图3 稳态下PWM整流器网侧相电压矢量关系图
图3中U、E、I分别是整流器交流侧基波相电压、网侧基波相电压、网侧相电流基波有效值。当网侧电压E不变,电流I固定时,电压U的轨迹在以电感电压的UL大小为半径的圆上,当电压U的端点分别在B和D时,对应的是单位功率因数的整流和逆变。由于PWM整流器可以实现四象限运行,可以得到式(3)[8]:
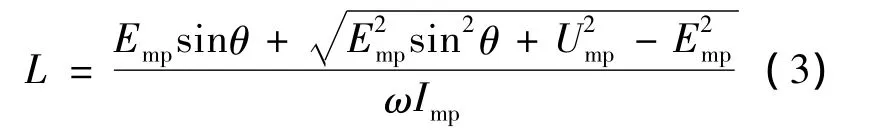
式中:Emp——网侧相电压峰值;
Ump——整流器交流侧基波电压有效值;
Imp——相电流峰值。
在采用SVPWM时,可以获得的基波电压峰值是Ump=Udc/,其中Udc是整流器直流母线电压。考虑到系统单功率因数运行,可以得到:
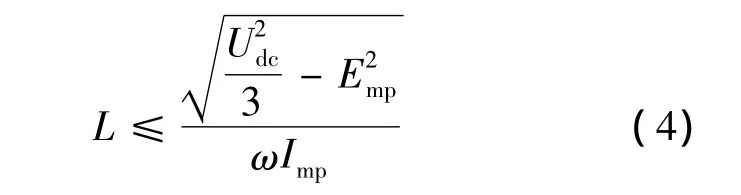
纹波电流的最大值[9]为
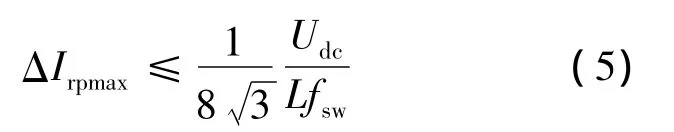
式中fsw是开关频率。综合式(4)和式(5)可得到:
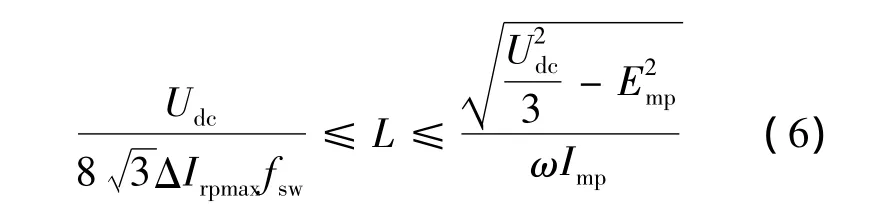
但是L的值取得过大,则系统的响应速度会变慢,因此电感L的选取要综合考虑所有因素来确定。
3.2 滤波电容C的选取
基波频率下对单相的LCL滤波器进行简化可以得到图4所示的电路图。
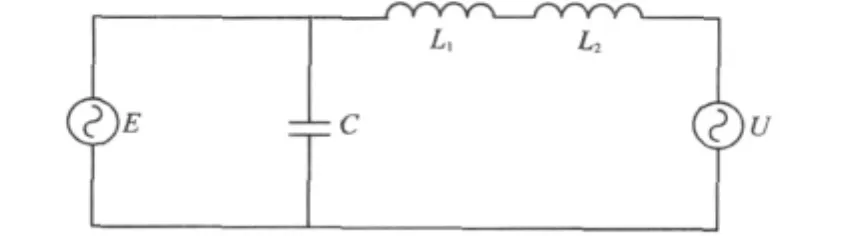
图4 LCL滤波器的基波等效电路
从图4可以得到:

式中:Qc——滤波电容吸收的无功功率;
λ——无功功率Qc相对于有功功率P的百分比。
3.3 滤波电感L1和L2的计算
对于谐波电流来说,网侧的电感呈现高阻抗性,大部分的谐波电流流经滤波电容支路。在电网电压理想的情况下(电网电压不含谐波),可以得到LCL滤波器的谐波等效电路,如图5所示。
从图5可以得出:
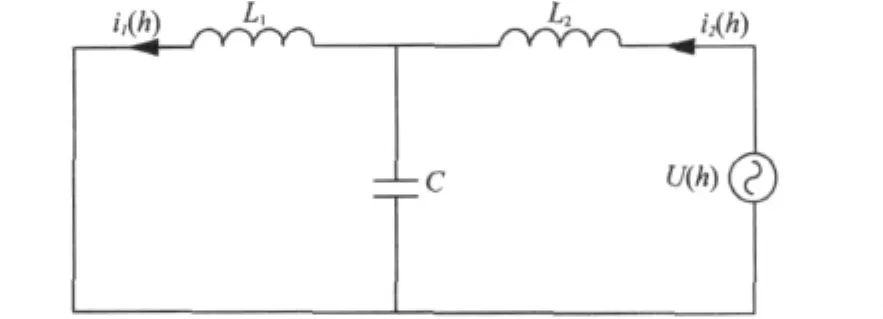
图5 LCL滤波器的谐波等效电路
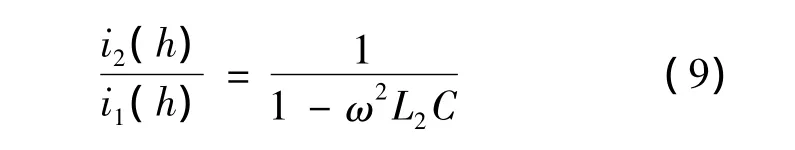
3.4 阻尼电阻的选取
从上面的分析可以得知,LCL滤波器存在谐振。本文是通过在滤波电容支路串联电阻的方法来实现抑制谐振的作用,电容支路串联电阻后,LCL滤波器的传递函数如式(10)所示:
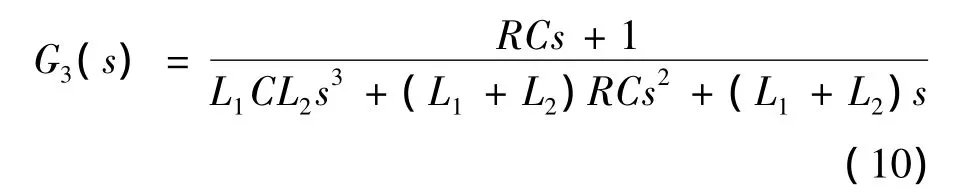
分别取不同的阻尼电阻,得到LCL滤波器的波特图如图6所示。
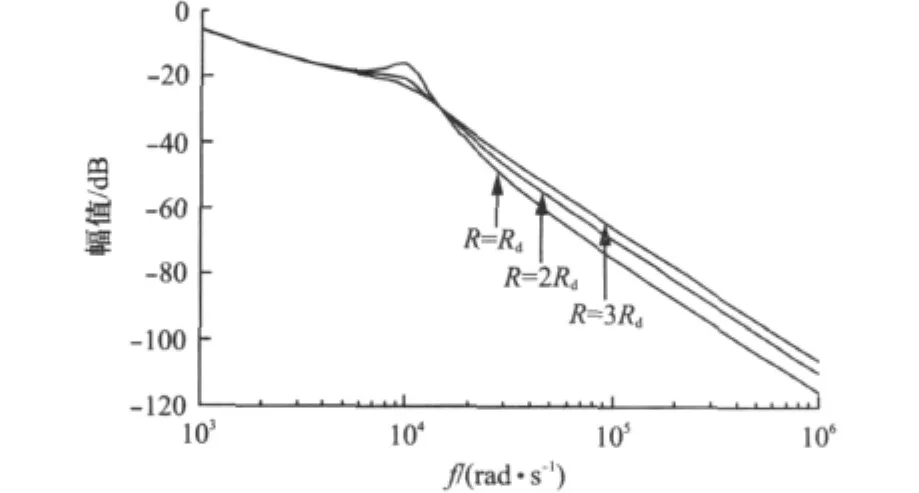
图6 LCL滤波器电容支路串联电阻的波特图
阻尼电阻R的引入增大了系统的阻尼比,很好地抑制了系统的谐振作用;并且对于电容支路串联电阻的方法,随着电阻的增大抑制谐振的作用更加明显。但是阻尼电阻的加入,会使滤波器的高频特性发生变化,电阻值越大高频段的衰减速度牺牲越大;同时阻尼电阻上的损耗也将增大,损耗值如式(11)所示:
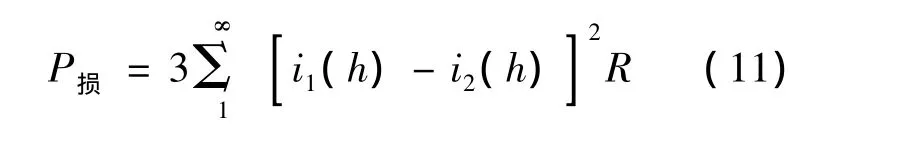
因此在选择阻尼电阻时应该综合考虑,以得到最合适的阻尼电阻。一般取阻尼电阻R的大小为谐振处电容阻抗的1/3,系统的波特图如图6中的R=Rd所示。
4 LCL滤波器设计实例及仿真验证
要求:功率2 kW,网侧额定电压有效值70 V,开关频率4 kHz,逆变器侧的纹波电流小于额定电流的20%,并网电路THD小于5%。
由式(5)可以得到总的滤波电感L大小为1.894 mH。为了得到更好的滤波效果,取电感的值为2 mH。由式(8)可以计算出滤波电容的值为20 uF。参照网侧滤波电感和逆变器侧电感的取值原则,得到网侧电感大小为0.8 mH,整流器侧电感的大小为1.2 mH,无源阻尼电阻R大小为1.63 Ω。
利用上面的参数在MATLAB/Simulink中搭建仿真电路对系统进行仿真,图7和图8分别是整流器交流侧和网侧电流波形。

5 结语
本文对LCL滤波器和L滤波器进行了比较,并详细阐述了LCL滤波器的设计原则,并给出了实例设计和仿真验证波形。结果表明,LCL滤波器能够更好地滤除高次谐波,达到相同的滤波效果时,LCL滤波器能够减小电感值,从而降低了成本、减小了电感的体积,因此在大功率场合有很大的应用前景和优势。
[1]林渭勋.现代电力电子技术[M].北京:机械工业出版社,2006.
[2]MARCO L,FREDE B,STEFFAN H.Design and control of an LCL filter—based three phase active rectifier[J].IEEE Transactions on Industry Applications,2005,41(5):1281-1290.
[3]LISERRE M,DELL A A,BLAABJERG F.Stability improvements of an LCL—filter based three—phase active rectifier[C]∥IEEE Annual Power Electronics Specialists Conference,2002(3):1195-1201.
[4]张宪平,李亚西,林资旭,等.LCL滤波的电压型PWM整流器的有源阻尼控制[J].电气传动,2007,37(11):22-25.
[5]TIMOTHY C Y W,ZHI H Y,GAUTAM S,et al.Output filters design for a grid-interconnected threephase inverter[C]∥ Power Electronics Specialist Conference,2003,2003 IEEE 34th Annual,2003(2):779-784.
[6]VLADIMIR B,VIKRAM K.A novel control to actively damp resonance in input LC filter of a threephase voltage source converter[J].IEEE Transactions on Industry Application,1997,33(2):542-550.
[7]LISERRE M,DELL A A,BLAABJERG F.Genetic algorithm based design of the active damping for a LCL—filter three—phase active rectifier[C]∥Annual IEEE Applied Power Electronics Conference and Exposition,2003(1):234-240.
[8]张崇巍,张兴.PWM整流器及其控制[M].北京:机械工业出版社,2005.
[9]PRASAD V H.Analysis and comparison of space vector modulation schemes for three-leg voltage source inverters[D].Blacksburg,VA:Virginia Polytechnic Institute and State University,1997.

